Решение варианта 11.

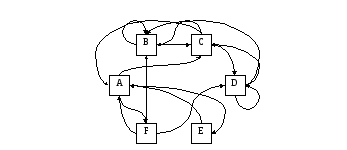
Обозначим через M матрицу смежности.

Произведение матрицы смежности орграфа
		A	B	C	D	E	F
	A	0	0	1	0	1	1
	B	0	1	1	0	0	0
M=	C	1	1	0	1	0	0
	D	0	1	1	1	0	0
	E	1	0	0	0	0	0
	F	1	1	0	1	0	0
		A	B	C	D	E	F
	A	1	1	0	1	0	0
	B	1	1	1	1	0	0
M2 =	C	0	1	1	1	1	1
	D	1	1	1	1	0	0
	E	0	0	1	0	1	1
	F	0	1	1	1	1	1
		A	B	C	D	E	F
	A	0	1	1	1	1	1
	B	1	1	1	1	1	1
M3 =	C	1	1	1	1	0	0
	D	1	1	1	1	1	1
	E	1	1	0	1	0	0
	F	1	1	1	1	0	0
		A	B	C	D	E	F
	A	1	1	1	1	0	0
	B	1	1	1	1	1	1
M4 =	C	1	1	1	1	1	1
	D	1	1	1	1	1	1
	E	0	1	1	1	1	1
	F	1	1	1	1	1	1
		A	B	C	D	E	F
	A	1	1	1	1	1	1
	B	1	1	1	1	1	1
M5 =	C	1	1	1	1	1	1
	D	1	1	1	1	1	1
	E	1	1	1	1	0	0
	F	1	1	1	1	1	1
		A	B	C	D	E	F
	A	1	1	1	1	1	1
	B	1	1	1	1	1	1
M6 =	C	1	1	1	1	1	1
	D	1	1	1	1	1	1
	E	1	1	1	1	1	1
	F	1	1	1	1	1	1
M6 – матрица достижимости

1. Составить три множества Ф, И, О из букв, соответственно, своей фамилии, своего имени и своего отчества.

2. Представить полученные множества на кругах Эйлера.

3. Представить буквы множеств Ф, И, О в двоичной системе, используя следующую кодировку

А	00001	Л	01011	Ц	10110
Б	00010	М	01100	Ч	10111
В	00011	Н	01101	Ш	11000
Г	00100	О	01110	Щ	11001
Д	00101	П	01111	Ъ	11010
Е	00110	Р	10000	Ы	11011
Ж	00111	С	10001	Ь	11100
З	01000	Т	10010	Э	11101
И	01001	У	10011	Ю	11110
К	01010	Ф	10100	Я	11111
		Х	10101

.

4. Используя 2, 3 и 4 разряды определить 3 булевые функции F1(x1, x2, x3, x4, x5), F2(x1, x2, x3, x4, x5), F3(x1, x2, x3, x4, x5), определенные на 5-разрядных двоичных числах (на буквах, не вошедших в Ф, И, О положить значение функции равной 0) .

5. Представить каждую функцию в совершенной дизъюнктивной нормальной форме (СДНФ).