7.3. Точные решения для притока упругой жидкости к прямолинейной галерее и к точечному стоку (источнику) на плоскости
За прямолинейную галерею можно принять любую прямолинейную изобару. Пусть в начальный момент t=0 первоначальное пластовое давление было всюду одинаковым Рк. Пусть на галерее (х=0) давление мгновенно упало до величины Рс. При этом в пласте тут же происходит перераспределение давления. Требуется найти функцию распределения давления Р=Р (х, t). Для этого необходимо решить уравнение для рассматриваемого одномерного прямолинейного движения
.
(7.30)
Начальные и граничные условия математически записываются в форме
,
.
(7.31)
Решение задачи (7.30), (7.31) хорошо известно и приведено, например, в [5, 6]. Оно имеет следующий вид:
(7.32)
(7.33)
(7.34)
Здесь
– интеграл
вероятности или интеграл Гаусса. Он
табулирован и имеется в справочниках.
Зная æ
и
t,
подсчитывают ,
затем по таблицам или графикам определяют
интеграл
и находят, таким образом, давление Р
в любой точке пласта в заданное время.
Далее рассмотрим задачу о притоке упругой жидкости к точечному стоку (источнику) на плоскости, т. е. в неограниченном пласте. При этом требуется решить уравнение Лапласа, которое в цилиндрических координатах запишется в виде
(7.35)
Имеется несколько методов решения уравнения (7.35). Например, метод Фурье, когда решение ищется в виде произведения независимых функций, метод сведения дифференциального уравнения в частных производных к обыкновенному дифференциальному уравнению [6] и др.
В конечном виде решение уравнения (7.35) для притока упругой жидкости к стоку на плоскости представляется выражением:
(7.36)
где
(7.37)
f0 – параметр Фурье.
Интегральная
показательная функция
табулирована и имеется в српавочниках.
Формула (7.36) является основной формулой теории упругого режима пласта, которая нашла широкое применение в практике разработки нефтяных месторождений.
Для малых значений аргумента f0 интегральная показательная функция приближенно может быть вычислена элементарно по формуле
(7.38)
Скорость фильтрации на расстоянии r определяется по формуле
(7.39)
В случае кругового пласта конечных размеров точные решения выражаются громоздкими в бесконечных рядах функциями Бесселя. Графики и таблицы для численных расчетов приведены Чатасом и Маскетом.
Заметим, что формула (7.36) справедлива лишь для точечного стока, т. е. для r=0. Однако, как показали анализы, этой формулой можно пользоваться не только для обычных скважин, но и для «укрупненных», радиус которых исчисляется десятками метров. Ограничение в применении формулы (7.36) может быть лишь для времени t в долях секунды от момента пуска скважины.
На рис. 7.3 изображены пьезометрические кривые для различных моментов времени после пуска скважины. Процесс распределения давления в пласте после пуска можно характеризовать следующим образом. Вокруг скважины, непрерывно увеличиваясь, образуется область, в пределах которой давление распределяется так, как и при установившемся движении. Такой процесс называется квазиустановившимся. В пределах этой области пьезометрические кривые являются кривыми логарифмического типа (на рисунке они показаны жирными отрезками), а углы наклона касательных к разным кривым для любой точки пласта (см. рис. 7.3) (такой точкой является забой скважины) одинаковы.
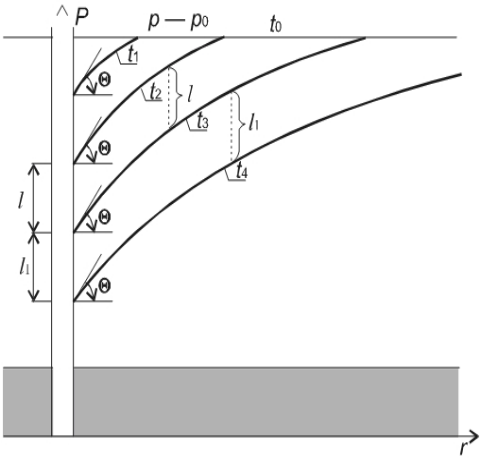
Рис.7.3. Пьезометрические кривые с участками квазиустановившегося