3.Плоские задачи теории фильтрации

3.1. Связь теории функции комплексного переменного с плоской задачей теории фильтрации. Функция тока. Комплексный потенциал

Для плоского движения несжимаемой жидкости потенциал является функцией двух координат, т. е. Ф=Ф(х, у).

Уравнения движения записываются в виде:

(3.1)

Уравнение неразрывности есть

(3.2)

Уравнение Лапласа

(3.3)

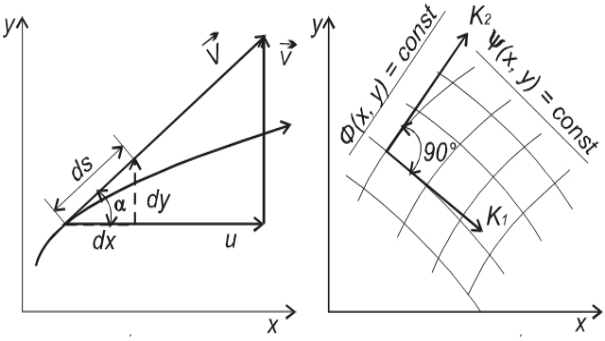
Найдем уравнение линий тока. Линией тока называется такая линия, касательная к которой в любой точке совпадает с вектором скорости. Отсюда следует выражение для направляющих косинусов (рис. 3.1):

или

откуда следует уравнение линий тока

(3.4)

Здесь

ds – элемент линии тока с проекциями dх и dу,

 – модуль вектора скорости с проекциями u и ;

α и β – углы между осями координат и вектором скорости .

Решение уравнения (3.4) будем искать в виде неявной зависимости

(3.5)

Уравнение (3.5) называется функцией тока. Основное свойство функции тока — это ее постоянство вдоль линии тока. Но с переходом от одной линии тока к другой значение функции тока y (х, у) меняется (рис. 3.2).

Рис. 3.1. Схема к определению напраляющих косинусов вектора скорости

Рис. 3.2 Интерпретация функции комплексного переменного на плоскости [Ф(х, у)=const – семейство эквтенциалей; y(х, у)=const – семейство линий тока]

Установим связь функции тока с потенциалом скорости фильтрации Ф (х, у)=С. Поскольку y (х, у)=const вдоль линии тока. то полный дифференциал ее равен нулю, т. е.

(3.6)

Это то же уравнение линий тока, что и (3.23), но только в неявной форме. Сравнивая (3.6) и (3.3), получаем:

(3.7)

Сравнивая (3.1) и (3.7), находим:

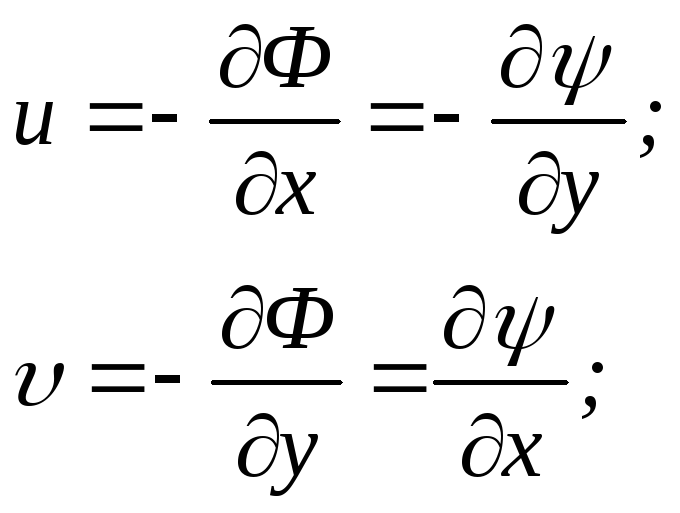
или

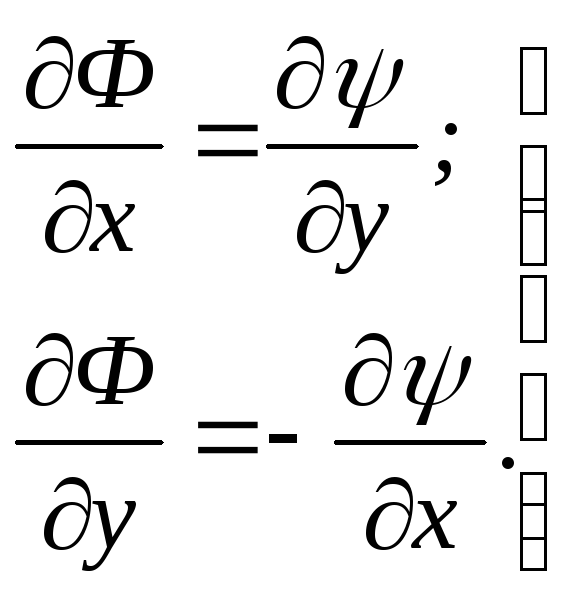(3.8)

Получили уравнения Коши-Римана, удовлетворяющие уравнению Лапласа.

3.2. Установившийся приток к группе совершенных скважин. Интерференция совершенных скважин

Интерференция скважин является одной из сложных задач подземной гидродинамики, представляющих несомненный интерес для теории и практики разработки нефтяных и газовых месторождений. Этой проблеме посвящено много работ как отечественных, так и зарубежных авторов.

Впервые теория взаимодействия скважин изложена В.Н. Щелкачевым и Г.Б. Пыхачевым (1939). Они подвели итоги исследовательских работ в этом направлении, проведенных в ГрозНИИ в 1935-1937 гг., и дали критический анализ ранее существовавших теорий интерференции скважин. Таким образом, теория взаимодействия скважин была фундаментально разработана советскими исследователями еще до появления книги Маскета (1937).

Дальнейшее развитие теории взаимодействия скважин нашло свое отражение в позднейших работах В.И. Щелкачева, Г.Б. Пыхачева, И.А. Чарного, А. П. Крылова и др.

Обычно месторождение эксплуатируется десятками и сотнями скважин. Все скважины в процессе работы интерферируют (взаимодействуют) между собой. Другими словами, работа одной скважины взаимно влияет на режим работы другой соседней скважины. При этом задача встречается в двух постановках: 1) задаются дебиты скважин (до известного предела) и требуется определить давления на забоях скважин, а также давления в различных точках пласта (пластовые давления); 2) задаются забойными давлениями и определяют дебиты скважин. Второй случай в практике используется чаще. Здесь также величина забойных давлений ограничивается технологическими условиями эксплуатации (например, выносом песка, давлением насыщения, смятием колонны и т. д.).

Хорошо известно, что рост суммарного дебита по месторождению отстает от роста числа скважин. Если поставить задачу обеспечения роста дебита пропорционально количеству скважин, то придется постоянно снижать забойное давление. Однако здесь также существует предел, до которого возможно снижать забойное давление.

Задача о расстановке и выборе сетки скважин, об определении необходимого количества скважин, обеспечивающих рациональную систему разработки нефтяного или газового месторождения, является весьма сложной и рассматривается в специальных курсах. Этому предшествуют сложные гидродинамические расчеты и расчеты технико-экономических показателей.

3.2.1. Потенциал группы точечных стоков на плоскости. Взаимодействие скважин. Рассмотрим плоскую задачу интерференции точечных стоков (совершенных скважин) при фильтрации несжимаемой жидкости по закону Дарси (рис. 3.3). При отсутствии отбора статический уровень будет всюду одинаков и равен (Р_к – давление на контуре питания). При создании депрессии DР=Р_к-Р_с (Р_с – давление на забое скважины) жидкость притекает к забоям скважин, статический уровень понижается и устанавливается так называемая «пьезометрическая воронка», схематическое изображение которой показано на рис. 3.4.

Далее возьмем неограниченную плоскость в плане и разместим на ней произвольное число стоков (источников) произвольным образом (рис. 3.5).

Требуется определить результирующий потенциал от взаимодействия потенциалов отдельных стоков (источников). В условиях линейного закона фильтрации результирующим потенциалом любой точки М будет алгебраическая сумма потенциалов отдельных стоков А₁, А₂, А₃, и т. д., т. е.

или

, (3.9)

где

(3.10)

Рис. 3.3. Схема взаимодействия стоков (источников) в