
Ценообразование кредитного риска с риском дефолта одной из сторон
Пусть Х(Т) – обещанная к выплате сумма долга, выплачиваемая по опциону европейского типа в момент Т. Если фирма – должник остается платежеспособной до момента Т включительно, то она выплачивает держателю опциона сумму Х(Т). Если в момент t<T наступает дефолт по платежам, то держатель опциона получает только часть от обещанного количества Х(Т). В этом случае размер выплаты зависит от текущей стоимости активов и обязательств. Пусть, как и ранее, V(t) – стоимость активов заемщика. Кроме того, пусть D(t) – стоимость обязательств фирмы. Тогда в случае банкротства фирма выплачивает банку следующую часть Х(Т):
![]() .
.
Дробь
![]() называют скорость восстановления
активов фирмы, или соотношением единицы
активов на единицу долга. Чем ближе оно
к нулю, тем быстрее фирма станет банкротом.
называют скорость восстановления
активов фирмы, или соотношением единицы
активов на единицу долга. Чем ближе оно
к нулю, тем быстрее фирма станет банкротом.
Обозначим
![]() .
Тогда сумма выплаты Хd
по опциону кредитного риска может быть
представлена в общем виде как:
.
Тогда сумма выплаты Хd
по опциону кредитного риска может быть
представлена в общем виде как:
![]() (*)
(*)
где
![]() - индексное множество,
- индексное множество,
![]() -
момент дефолта.
-
момент дефолта.
Из (*) видно, что при банкротстве в момент τ>T банк получает Х(Т) (момент банкротства не влияет в этом случае на выплаты), а при τ≤Т выплачивается часть долга δ(T)X(T).
Заметим, что в случае δ(T)>1, или при V(T)>D(T), долг Х(Т) будет полностью погашен, даже если наступит дефолт по обязательствам. Если V(T)<D(T), то долг оплачивается с коэффициентом пропорциональности δ(T). Поэтому равенство (*) эквивалентно следующему выражению:
![]()
Мы знаем, что цена опциона европейского типа C(t) с функцией выплаты f(T) находится по формуле:
![]() ,
,
где Е* - риск – нейтральное математическое ожидание, Bt=B0erT≡1 – цена облигации с безрисковой процентной ставкой (единица капитала), Ft – фильтрация.
В нашем случае выплата f(T)=Xd(T), поэтому
![]() (3)
(3)
(не забыть вывести уравнение Б - Ш для vulnerable option).
Теорема 1 (о цене опциона покупателя кредитного риска или незащищенного опциона, vulnerable):
Пусть Х(Т) – цена незащищенного опциона с функцией выплаты XT=(ST – Е)+ и выплачиваемой в действительности суммой XT= δ(T)(ST – Е)+. Тогда в случае банкротства:
![]()
![]() ,
где
,
где
![]() ,
D-размер
долга, E
– цена исполнения опциона,
,
D-размер
долга, E
– цена исполнения опциона,
![]() ,
,
![]() ,
,
![]() ,
,
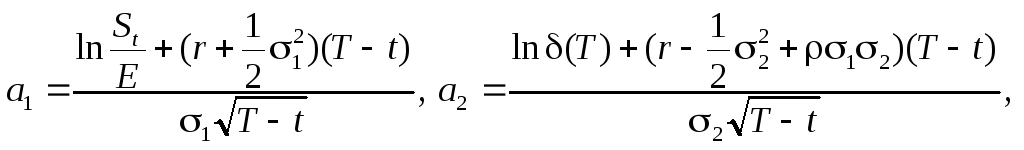
![]()
![]()
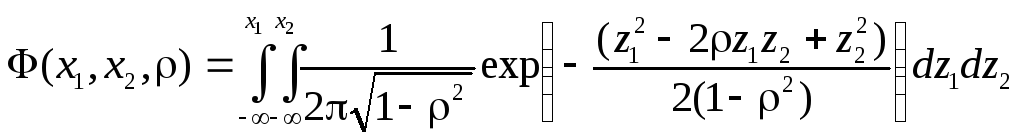 -
двумерная функция распределения
нормальной СВ.
-
двумерная функция распределения
нормальной СВ.
Доказательство теоремы громоздко и основано на непосредственном вычислении математического ожидания в (3).
Рассмотрим
стохастическое дифференциальное
уравнение, соответствующее незащищенному
опциону с функцией выплаты (3). Очевидно,
![]() ,
то есть является функцией переменных
S,V,
t.
,
то есть является функцией переменных
S,V,
t.
Пусть S,V – процессы Ито, то есть:
![]()
Применим
двумерную формулу Ито к
![]() .
Имеем:
.
Имеем:
![]() .
Так как
.
Так как
![]() ,
то окончательно имеем:
,
то окончательно имеем:
![]() (4)
(4)
По
аналогии с идеей Блэка – Шоулса, составим
хеджирующий портфель, чтобы избавиться
от стохастической части в (4). Пусть Н
– хеджирующий портфель, H=F-∆1V-∆2S,
или, как при ∆ - хеджировании,
![]() .
Тогда
.
Тогда
![]() ,
подставляя которое в (4), имеем:
,
подставляя которое в (4), имеем:
![]() .
(5)
.
(5)
Изменения в хеджирующем портфеле зависят
теперь только от dt,
он безрисковый и, как альтернатива, его
можно инвестировать под ставку r.
Тогда dH
= rHdt,
или так как
![]() .
Поэтому в (5):
.
Поэтому в (5):
![]() .
.
Окончательно,
![]() (6)
(6)
Это 2d уравнение Блэка – Шоулса, где F = Xd(t), которое с точностью до обозначений совпадает с уравнением для стохастической волатильности.
Замечание: При δ(t)≡1 для каждого tЄ[0,T] весь долг обеспечен суммой активов Vt. Поэтому цена незащищенного опциона Хd(t) будет равна цене опциона без кредитного риска, то есть обычного опциона покупателя. Чтобы убедиться в этом, достаточно подставить δ=1 в формулировку теоремы 1 о цене незащищенного опциона. При δ=1 формула расчета цены превращается в формулу Блэка – Шоулса. (Доказать самим)
