Билет 8, 17

Дать определения абсолютной и относительной сходимости знакопеременного ряда. Доказать теорему о сходимости абсолютно сходящегося знакопеременного числового ряда.

Ряд 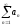называется знакопеременным, если среди членов ряда содержится бесконечное количество отрицательных членов и бесконечное количество положительных членов.

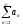Ряд называется абсолютно сходящимся, если ряд из модулей членов ряда 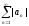сходится.

Теорема. Если ряд абсолютно сходится, то он сходится.

Доказательство. Так как ряд 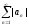сходится, то ряд тоже сходится. Ряд 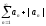- знакоположительный, так как 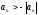и сходится по первому признаку сравнения рядов по сравнению со знакоположительным рядом , так как 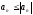. Вычитая из сходящегося ряда 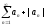сходящийся ряд 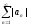, получаем сходящийся ряд (свойство сходящихся рядов) .

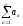Билет 9,18

Дать определение сходящегося числового ряда. Вывести простейшие свойства сходящихся числовых рядов.

Числовой ряд – это сумма бесконечного количества чисел, выбранных по определенному алгоритму. Обычно задают формулу общего члена ряда .

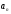Ряд 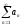называется сходящимся, если существует конечный предел последовательности частичных сумм ряда – он называется суммой ряда .

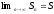Ряд называется расходящимся, если предел частичных сумм ряда бесконечен или вообще не существует.

Свойства сходящихся рядов.

1. Члены сходящегося ряда можно умножить на одно и то же число k. Полученный ряд будет сходиться, а сумма его будет в k раз больше суммы исходного ряда.

Доказательство. Для второго ряда частичная сумма будет равна 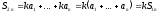. По теореме о предельном переходе в равенстве .

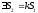2. Члены сходящегося ряда можно группировать. Полученный ряд будет сходиться, и сумма его не изменится.

Сгруппируем члены ряда, например, так

. Видно, что частичные суммы группированного ряда представляют собой подпоследовательность последовательности частичных сумм исходного ряда. Так как последовательность сходится, то и подпоследовательность сходится к тому же пределу.

3. В сходящемся ряде можно отбросить конечное число первых членов 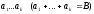. Полученный ряд будет сходиться, а его сумма будет меньше суммы исходного ряда на B.

Запишем частичные суммы второго ряда 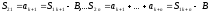. По теореме о предельном переходе в равенстве .

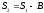Замечание. Ряд, полученный из исходного ряда отбрасыванием первых k членов, называется остатком ряда и обозначается

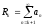
4. Для того чтобы ряд сходился необходимо и достаточно, чтобы сходился остаток ряда. (Докажите это самостоятельно, используя доказательство свойства 3).

Поэтому сходимость ряда можно исследовать, «начиная с некоторого n».

5. Сходящиеся ряды можно складывать (или вычитать), получая сходящийся ряд с суммой, равной сумме (или разности) сумм исходных рядов.

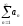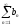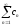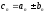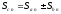Рассмотрим два сходящихся ряда и . Рассмотрим ряд , где . . Переходя к пределу в равенстве, получим .