
Билет 1,10,19
Доказать признак Лейбница сходимости знакочередующегося числового ряда. Оценка суммы и остатка ряда, удовлетворяющего признаку Лейбница.
Признак Лейбница.
Пусть
-
ряд
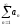 имеет
вид
имеет
вид
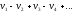 (знакочередующийся,
(знакочередующийся,
 )
) -
последовательность
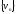 монотонно
убывает
монотонно
убывает -
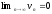
Тогда
1) ряд
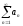 сходится
сходится
2)

Доказательство. Рассмотрим последовательность частичных сумм с четными номерами
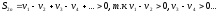 (последовательность
(последовательность
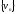 монотонно убывает по условию теоремы).
монотонно убывает по условию теоремы).

Т.е.
последовательность
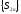 ограничена сверху
ограничена сверху
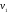 .
.
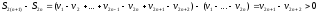
Т.е.
последовательность
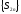 монотонно
возрастает.
монотонно
возрастает.
По
теореме Вейерштрасса существует
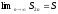 .
.
Рассмотрим теперь последовательность частичных сумм с нечетными номерами
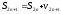 .
.
По
условию
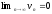 ,
т.е.
,
т.е.
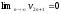 .
.
По
доказанному выше
 .
Следовательно, предел правой части
равенства существует и равен
.
Следовательно, предел правой части
равенства существует и равен
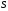 .
Поэтому предел левой части равенства
тоже существует и равен
.
Поэтому предел левой части равенства
тоже существует и равен
![]() .
.
Раскроем
определение предела
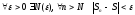 как для четных n, так и для
нечетных n. Следовательно,
это справедливо для любых
как для четных n, так и для
нечетных n. Следовательно,
это справедливо для любых
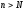 ,
поэтому
,
поэтому
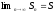 .
.
Из
доказанного выше неравенства
 .
Переходя к пределу, получим
.
Переходя к пределу, получим
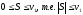 .
.
Следствие.
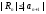 .
Остаток ряда оценивается модулем
первого отброшенного члена ряда.
.
Остаток ряда оценивается модулем
первого отброшенного члена ряда.
Доказательство. Так как остаток знакочередующегося ряда тоже знакочередующийся ряд, то его сумма по признаку Лейбница оценивается модулем его первого члена.
То
есть
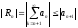 .
А первый член остатка ряда и есть первый
отброшенный член.
.
А первый член остатка ряда и есть первый
отброшенный член.
Билет 2,11,20
Вывести радикальный признак Коши сходимости знакоположительного числового ряда.
Конечная форма радикального признака Коши.
Пусть
 ,
тогда ряд
,
тогда ряд
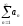 сходится.
сходится.
Пусть
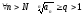 ,
тогда ряд
,
тогда ряд
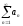 расходится.
расходится.
Доказательство.
Пусть
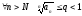 .
Тогда
.
Тогда
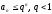 ,
ряд
,
ряд сходится
по первому признаку сравнения с бесконечно
убывающей геометрической прогрессией.
сходится
по первому признаку сравнения с бесконечно
убывающей геометрической прогрессией.
Пусть
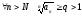 .
Тогда
.
Тогда
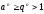 ,
ряд
,
ряд
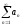 расходится,
так как необходимый признак сходимости
ряда не выполнен.
расходится,
так как необходимый признак сходимости
ряда не выполнен.
Предельная форма радикального признака Коши.
Пусть
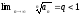 ,
тогда ряд
,
тогда ряд
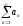 сходится.
сходится.
Пусть
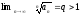 ,
тогда ряд
,
тогда ряд
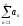 расходится.
расходится.
Доказательство.
Пусть
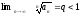 ,
тогда
,
тогда
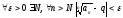 .
.
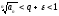 при
малом
при
малом
 .
Ряд
.
Ряд
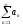 сходится
по конечной форме радикального признака
Коши.
сходится
по конечной форме радикального признака
Коши.
Пусть
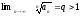 ,
тогда
,
тогда
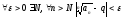 .
.
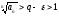 при малом
при малом
 .
Тогда
.
Тогда
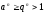 ,
ряд
,
ряд
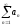 расходится,
так как необходимый признак сходимости
ряда не выполнен.
расходится,
так как необходимый признак сходимости
ряда не выполнен.
Билет 3, 12, 21
Дать определения равномерной сходимости функционального ряда. Доказать признак Вейерштрасса равномерной сходимости функционального ряда.
Функциональный
ряд
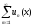 называется равномерно сходящимся в
области V, если
называется равномерно сходящимся в
области V, если
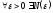 ,
что
,
что
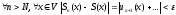 .
.
Здесь
номер N зависит только от
 ,
но не от точки x, поэтому
номер N выбирается сразу
для всей области V. Ряд
сходится с одной и той же скоростью для
всех точек области V. Такая
сходимость напоминает сходимость
числовых рядов. Действительно, равномерно
сходящиеся ряды обладают очень полезными
свойствами, которые мы обсудим ниже.
,
но не от точки x, поэтому
номер N выбирается сразу
для всей области V. Ряд
сходится с одной и той же скоростью для
всех точек области V. Такая
сходимость напоминает сходимость
числовых рядов. Действительно, равномерно
сходящиеся ряды обладают очень полезными
свойствами, которые мы обсудим ниже.
Критерий Коши равномерной сходимости ряда.
Для
того чтобы функциональный ряд
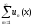 равномерно сходился в области V,
необходимо и достаточно, чтобы
равномерно сходился в области V,
необходимо и достаточно, чтобы
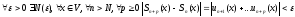 .
.
Признак Вейерштрасса равномерной сходимости ряда.
Пусть
члены функционального ряда
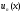 можно
мажорировать (ограничить по модулю) в
области V членами сходящегося
числового знакоположительного ряда,
можно
мажорировать (ограничить по модулю) в
области V членами сходящегося
числового знакоположительного ряда,
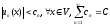 .
.
Тогда
функциональный ряд
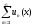 равномерно
сходится в области V.
равномерно
сходится в области V.
Доказательство.
Так как числовой ряд сходится, то для
него выполнен критерий Коши
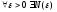
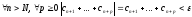 (ряд знакоположителен,
(ряд знакоположителен,
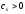 ).
).
Тогда
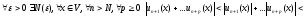
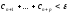 .
.
Следовательно,
выполнен критерий Коши равномерной
сходимости ряда, и ряд
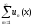
 сходится
в области V равномерно.
сходится
в области V равномерно.
