Нахождение скалярного произведения через координаты векторов

(3.7).

Пример 3.4. Даны координаты векторов и . Найти их скалярное произведение.

Решение. По формуле (3.7) получим: .

Приложения скалярного произведения векторов

1) Если , то угол между ними:

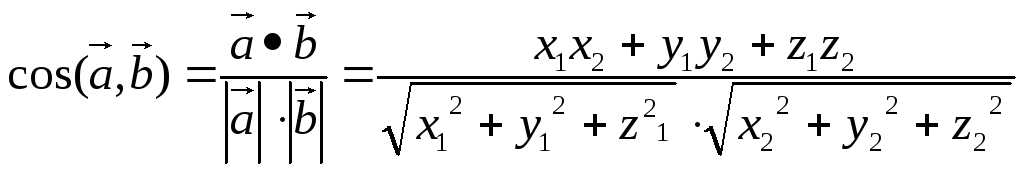(3.8).

2) (3.9).

Пример 3.5. Даны координаты векторов и . Найти косинус угла между ними.

3.5. Векторное произведение векторов

Векторным произведением двух векторов и называется третий вектор , удовлетворяющий следующим трем условиям:

1);

2) и ;

3) вектора образуют правую тройку (т.е. если смотреть с конца вектора , то кротчайший поворот от вектора к вектору совершается против часовой стрелки).

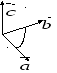
Векторное произведение обозначается: .

Свойства векторного произведения векторов:

1.	4.
2.	5.
3.

Нахождение векторного произведения через координаты векторов

Если и , то

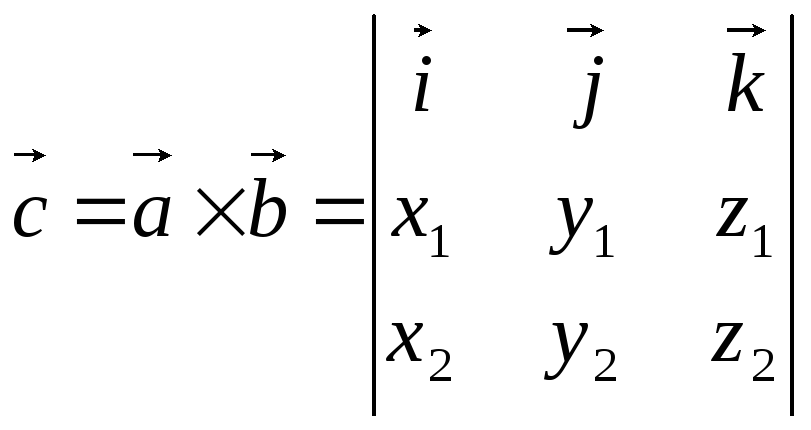(3.10).

или = 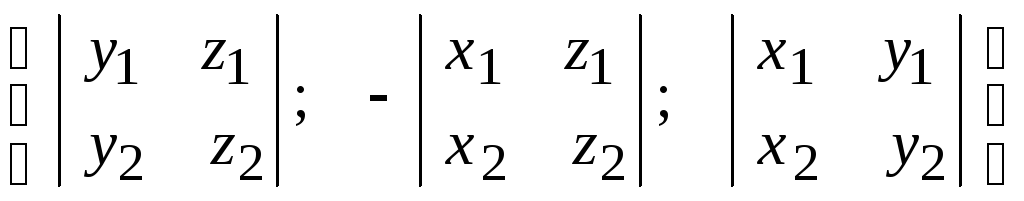(3.11).

Приложения векторного произведения векторов

1. Площадь параллелограмма построенного на векторах и :

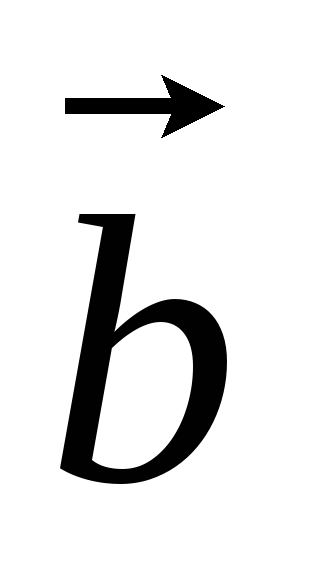S_парал.= (3.12).

2. Площадь треугольника построенного на векторах и :

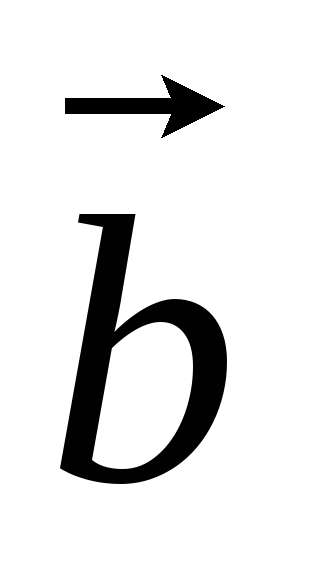S_треуг.= (3.13).

Пример 3.6. Найти площадь параллелограмма построенного на векторах и , где , .

3.6. Смешанное произведение векторов

Смешанным произведением трёх векторов называется число равное скалярному произведению вектора на векторное произведение векторов и

Смешанное произведение обозначается и по определению равно:

_(3.14).

Свойства смешанного произведения векторов:

1. ;

2. ;

3.;

4.;

5. (не нарушается круговой порядок);

6. (нарушается круговой порядок).

Нахождение смешанного произведения через координаты векторов

Если то

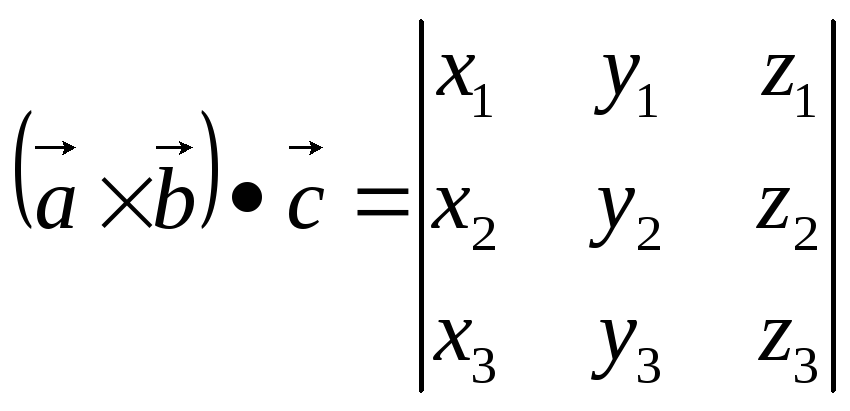(3.15).

Приложения смешанного произведения векторов

1. Объем параллелепипеда построенного на векторах :

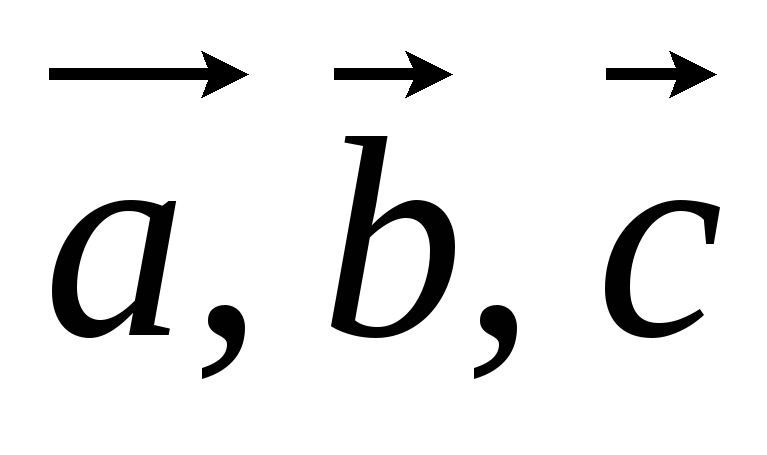V_парал. = (3.16).

2. Объем пирамиды построенной на векторах :

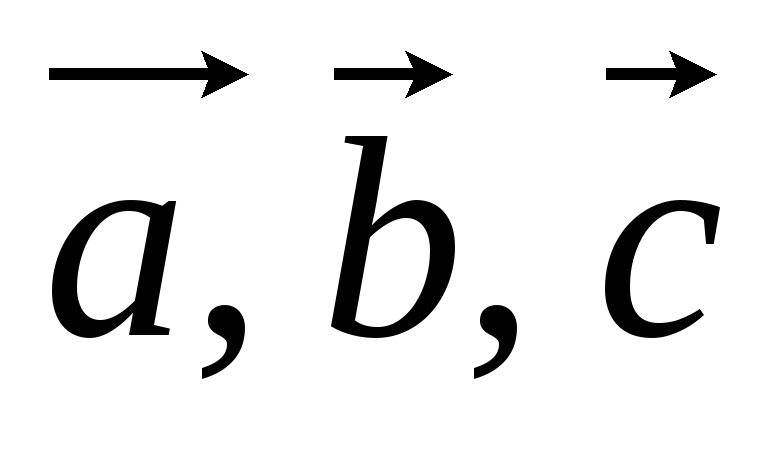V_пир. = (3.17).

3. Признак компланарности трех векторов (линейной зависимости трех векторов): если 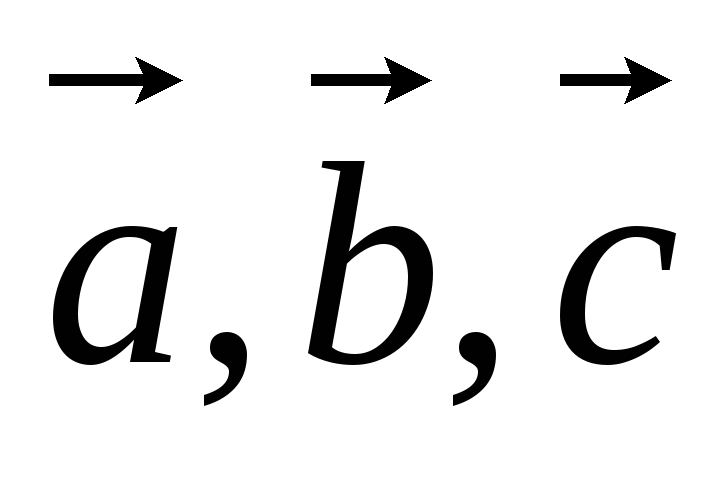компланарны (линейно зависимы),

или 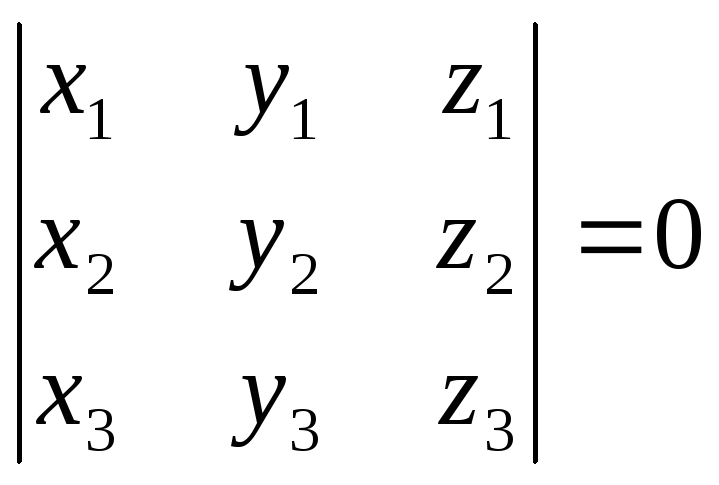(3.18).

Пример. Найти объем параллелепипеда построенного на векторах , где , , .

Пример. Пусть в магазине имеется набор из 5 товаров, количество и стоимость (в тыс. руб.) которых указана в таблице

Товар	1	2	3	4	5
Количество	50	150	75	100	200
Стоимость	35	40	70	80	20

Требуется определить общую стоимость товара в магазине.

Решение. Введём в рассмотрение вектор , координатами которого являются количество i – го товара (i = 1,2,3,4,5) и вектор , образованный из цен на эти товары. Тогда искомую общую стоимость S можно найти по формуле

Пример. На предприятии имеется шесть цехов. Плановые задания цехов (в млн. руб.) образуют вектор план

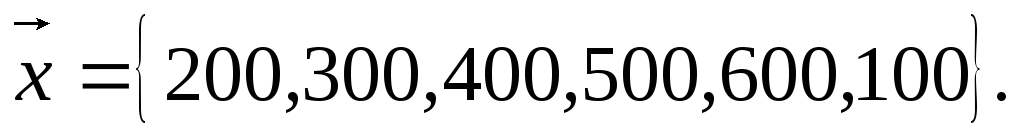
Предположим, что к какому-то моменту цехи выполнили свои планы соответственно на 20%,40%.50%,70%,30%,10%.Определить стоимость S произведенной предприятием продукции на данный момент.

Решение.

Если ввести в рассмотрение вектор выполнения плана,

то имеем

2. Определение вектора. Отрезок прямой задается дву­мя равноправными точками —его концами. Но можно рассматривать направленный отрезок, определяемый упо­рядоченной парой точек. Про эти точки известно, какая из них первая (начало), а какая вторая (конец).

Определение 1. Направленный отрезок (или, что то же, упорядоченную пару точек) мы будем называть вектором. Направление на отрезке принято отмечать стрелкой. Над буквенным обозначением вектора при письме ста­вится стрелка, например: (при этом буква, соответст­вующая началу вектора, обязательно ставится впереди). В книгах часто буквы, обозначающие вектор, набираются полужирным шрифтом, например: а.

К векторам будем относить и так называемый нулевой вектор, у которого начало и конец совпадают.

Вектор, начало которого совпадает с его концом, называют нулевым: Нулевой вектор обозначается или просто 0.

= .

Расстояние между началом и концом вектора называ­ется его длиной (а также модулем и абсолютной величи­ной). Длина вектора обозначается || или ||. Длиной вектора, или модулем вектора, называют длину соответствующего направленного отрезка: = .

Векторы называются коллинеарными, если они распо­ложены на одной прямой или на параллельных прямых, короче говоря, если существует прямая, которой они параллельны.

Векторы называются компланарными, если существует плоскость, которой они параллельны, их можно изобразить векторами, лежащими на одной плоскости. Нулевой вектор считается коллинеарным любому вектору, так как он не имеет определенного направления. Длина его, разумеется, равна нулю. Очевидно, любые два вектора компланарны; но, конечно, не каждые три вектора в пространстве компланарны. Так как векторы, параллельные друг другу, параллельны одной и той же плоскости, то коллинеарные векторы подавно компланарны. Разумеется, обратное неверно: компланарные векторы могут быть и не коллинеарными. В силу принятого выше условия нулевой вектор коллинеарен со всяким вектором и компланарен со всякой парой векторов, т.е. если среди трёх векторов хотя бы один нулевой, то они компланарны.

Определение 2. Два вектора называются равными, если они коллинеарны, одинаково направлены и имеют равные длины.

Необходимо всегда помнить, что равенство длин двух векторов ещё не означает равенства этих векторов.

По самому смыслу определения, два вектора, порознь равные третьему, равны между собой. Очевидно, все нулевые векторы равны между собой.

Из этого определения непосредственно вытекает, что, выбрав любую точку А', мы может построить (и притом только один) вектор А' В', равный некоторому заданному вектору , или, как говорят, перенести вектор в точку А' .

Замечание. Для векторов нет понятий «больше» или «меньше», т.е. они равны или не равны.

Вектор, длина которого равна единице, называется единичным вектором и обозначается через е. Единичный вектор, направление которого совпадает с направлением вектора а, называется ортом вектора и обозначается а.