ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ

Скалярные и векторные величины

1. При изучении различных разделов физики, механики и технических наук встречаются величины, которые полностью определяются заданием их числовых значений, более точно, которые полностью определяются при помощи числа, полученного в результате их измерения однородной величиной, принятой за единицу. Такие величины называются скалярными или, короче, скалярами. Ска­лярными величинами, например, являются длина, площадь, объ­ем, время, масса, температура тела, плотность, работа, электроёмкость и др. Так как скалярная величина определяется числом (положительным или отрицательным), то ее можно откладывать на соответствующей координатной оси. Так например, часто стро­ят ось времени, температуры, длины (пройденного пути) и другие.

Помимо скалярных величин, в различных задачах встречаются величины, для определения ко­торых, кроме числового значения, необходимо знать также их направление в пространстве. Такие величины называются векторными. Физиче­скими примерами векторных величин могут служить смещение материальной точки, двигающейся в пространстве, скорость и ускорение этой точки, а также действующая на нее сила, напряженность электрического или магнитного поля. Век­торные величины используются, например, и в климатологии. Рассмотрим простой пример из климатологии. Если мы скажем, что ветер дует со скоростью 10 м/с, то тем самым введем скаляр­ную величину скорости ветра, но если мы скажем, что дует се­верный ветер со скоростью 10 м/с, то в этом случае скорость ветра будет уже векторной величиной.

Векторные величины изображаются с помощью векторов.

Для геометрического изображения векторных величин слу­жат направленные отрезки, то есть отрезки, имеющие фикси­рованное направление в пространстве. При этом длина отрез­ка равна числовому значению векторной величины, а его на­правление совпадает с направлением векторной величины. Направленный отрезок, характеризующий данную векторную величину, называют геометрическим вектором или просто вектором.

Понятие вектора играет большую роль как в математике, так и во многих областях физики и механики. Многие физические величины могут быть представлены при помощи векторов, и это представление очень часто способствует обобщению и упрощению формул и результатов. Часто векторные величины и векторы, их изображающие, отождествляются друг с другом: так, например, говорят, что сила (или скорость) есть вектор.

Элементы векторной алгебры применяются в таких дисциплинах как: 1) электрические машин; 2) автоматизированный электропривод; 3) электроосвещение и облучение; 4) неразвлетвлённые цепи переменного тока; 5) прикладная механика; 6) теоретическая механика; 7) физика; 8) гидравлика:9) детали машин; 10) сопромат; 11) управление; 12) химия; 13) кинематика; 14) статика

Раздел II. Основы векторной алгебры

Глава 3. Векторы

3.1. Основные понятия

Вектор является математической моделью, которая используется, чтобы представить векторные величины, т.е. величины которые характеризуются не только своей величиной, но и направлением.

В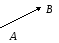ектором называется направленный отрезок ( = ) с начальной точкой А и конечной точкой В.

Длиной (или модулем) вектора (или ) называется число, равное длине отрезка АВ и обозначается или .

Вектор, модуль которого равен единице, называется единичным вектором.

Вектор, длина которого равна нулю, называется нулевым вектором. Нулевой вектор изображается точкой и обозначается , где . Направление нулевого вектора произвольно.

Вектора, лежащие на одной прямой или на параллельных прямых, называются коллинеарными.

Если коллинеарные векторы имеют одно и то же направление, то их называют сонаправленными.

Два вектора называются равными, если выполнены следующие условия:

1) векторы имеют одинаковую длину;

2) они коллинеарны;

3) сонаправлены.

Противоположным вектору называется вектор, который обознается и удовлетворяет следующим двум условиям:

1) ;

2) .

Угол между векторами и - это наименьший угол между ними, если совместить их точки.

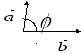
Если , то вектора и называются ортогональными, т.е. .

3.2. Линейные операции над векторами

Умножение вектора на число. Произведением вектора на действительное число  называется вектор такой, что . Вектор удовлетворяет следующим условиям:

1) ;

2) направление вектора совпадает с направлением вектора , если положительное, и противоположно ему, если отрицательное число;

3) .

Свойства:

 ;

 ;

 ;

 .

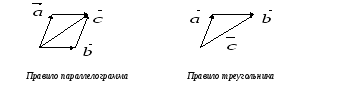
Сложение векторов. Суммой векторов и называется вектор =+, начало которого совпадает с началом вектора , а конец – с концом вектора , при условии, что начало вектора совпадает с концом вектора (правило треугольников).

Очевидно, что вектор в этом случае представляет диагональ параллелограмма, построенного на векторах и (правило параллелограмма).

Свойства:

	
	

Вычитание векторов. Разностью двух векторов и называется =, т.е. .

Таким образом, разностью векторов и называется вектор , начало которого совпадает с началом вектора , а конец – с концом вектора , противоположного .



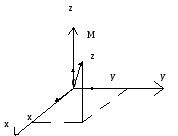
3.3. Координаты вектора

Координатами вектора называются координаты его конечной точки.

Например, координатами вектора = на плоскости Оху являются два числа х и у, а в пространстве Охуz – три числа х, у, z.

Нахождение координат вектора через координаты начальной и конечной точек. Пусть и . Имеем

(3.1).

Таким образом, координаты вектора можно найти, вычитая из координат конечной точки соответствующие координаты начальной точки вектора.

Пример 3.1. Пусть даны координаты точек и . Найдем координаты вектора

Решение. Используем формулу (3.1):

Тогда

Линейные операции над векторами в координатной форме

Пусть и

Тогда

1) ;

2) ;

3) т.е. .

Пример. 3.2. Найти координаты вектора , если .

Решение. .

Длина (модуль) вектора заданного координатами

Если , то длина (модуль) вектора:

(3.2).

Расстояние между двумя точками и

АВ = (3.3).

Пример 3.3. Даны координаты точек и . Найти расстояние между ними.

Направляющие косинусы вектора

Пусть – углы, которые образует вектор с осями координат Ox, Oy, Oz соответственно.

Тогда называются направляющимися косинусами вектора :

(3.4).

Следствия:

1)

2)

3.4. Скалярное произведение векторов

Скалярным произведением двух векторов и называется число, равное произведению длин этих векторов на косинус угла между ними:

(3.5).

Свойства скалярного произведения векторов:

1.	4.
2.	5.
3.	6.

Проекцией вектора на вектор называется число, равное

(3.6).