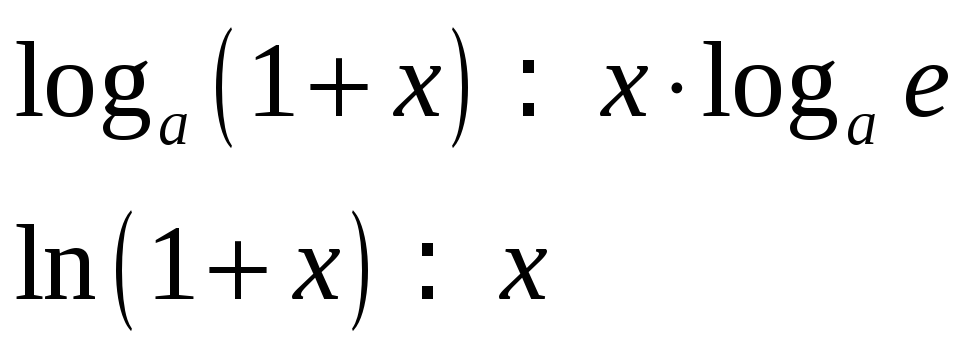- •Комплексные числа
- •Операции над комплексными числами
- •2. Числовые последовательности
- •3. Понятие функции. Предел и непрерывность функции
- •Методы раскрытия неопределённостей при вычислении пределов функций
- •Эквивалентные бесконечно малые величины
- •Непрерывность функции. Классификация точек разрыва
- •Классификация точек разрыва
- •4. Производная и дифференциал функции
- •Правила дифференцирования
- •Дифференциал функции
- •Производные высших порядков
- •Применение производной в экономике. Эластичность функции
- •5. Применение производной к исследованию функций Возрастание и убывание функций. Локальный экстремум функции
- •Наибольшее и наименьшее значения функции
- •Правила Лопиталя для раскрытия неопределенностей
- •Выпуклость, вогнутость и точки перегиба графика функции
- •Асимптоты графика функции
- •Исследование функций и построение графиков
- •Примерные варианты контрольной работы № 1 по математическому анализу
- •6. Неопределённый интеграл Первообразная. Неопределённый интеграл
- •Основные методы интегрирования Метод разложения
- •Метод замены переменной. Подведение под знак дифференциала
- •Метод интегрирования по частям
- •Интегрирование дробно-рациональных выражений
- •Метод неопределённых коэффициентов
- •Интегрирование иррациональных функций
- •Интегрирование тригонометрических функций
Эквивалентные бесконечно малые величины
Пусть
![]() и
и
![]() бесконечно малые функции при
бесконечно малые функции при
![]() Если
Если
![]() то
то
![]() и
и
![]() называются эквивалентными
бесконечно малыми
(обозначение:
называются эквивалентными
бесконечно малыми
(обозначение:
![]()
При
нахождении предела отношения двух
бесконечно малых можно каждую из них
(или только одну) заменить другой более
простой бесконечно малой, ей эквивалентной,
то есть если
![]()
![]() то
то
![]()
При
![]() имеют место следующие эквивалентности:
имеют место следующие эквивалентности:
|
|
|
|
|
|
|
|
|
|
|
|
Пример.
Вычислить
![]()
Решение.
Возникает неопределенность
![]() .
Заменим бесконечно малые функции в
числителе и в знаменателе на эквивалентные
бесконечно малые:
.
Заменим бесконечно малые функции в
числителе и в знаменателе на эквивалентные
бесконечно малые:
![]()
![]() при
при
![]()
Получим:
![]() .
.
Непрерывность функции. Классификация точек разрыва
Функция
![]() ,
определённая в точке а,
называется непрерывной в этой точке,
если
,
определённая в точке а,
называется непрерывной в этой точке,
если
![]() .
По аналогии с понятием одностороннего
предела, существует понятия функции,
непрерывной в точке справа и слева.
Функция непрерывна в данной точке тогда
и только тогда, когда она непрерывна
как слева, так и справа в этой точке.
.
По аналогии с понятием одностороннего
предела, существует понятия функции,
непрерывной в точке справа и слева.
Функция непрерывна в данной точке тогда
и только тогда, когда она непрерывна
как слева, так и справа в этой точке.
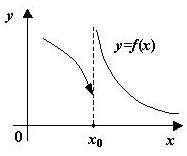
Пусть функция определена в некоторой окрестности точки а, может быть, за исключением самой точки а. Точка а называется точкой разрыва, если эта функция либо не определена в точке а, либо определена, но не является непрерывной в точке а.
Чаще всего разрыв возникает по двум причинам: 1) функция задана различными выражениями на разных участках, и в граничных точках эти выражения имеют различные пределы; 2) функция не определена в данной точке.
Классификация точек разрыва
Пусть
![]() - точка разрыва функции
- точка разрыва функции
![]() .
.
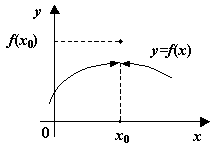
1. Устранимый разрыв I рода.
Если
в точке
![]() существуют односторонние пределы,
которые равны между собой, но не равны
значению функции в этой точке
существуют односторонние пределы,
которые равны между собой, но не равны
значению функции в этой точке
![]() или
или
![]() ,
а
,
а
![]() не
существует, то такая точка разрыва
называется устранимой.
не
существует, то такая точка разрыва
называется устранимой.
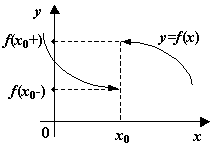
2. Неустранимый разрыв I рода.
Если
односторонние пределы в точке
![]() не равны между собой
не равны между собой
![]() ,
то такая точка разрыва называется
неустранимой.
,
то такая точка разрыва называется
неустранимой.
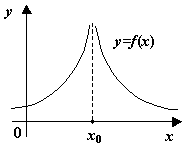
3. Разрыв II рода.
Если
хотя бы один из пределов
![]() и
и
![]() не существует или бесконечен в точке
не существует или бесконечен в точке
![]() ,
то такая точка называется точкой
разрыва II
рода.
,
то такая точка называется точкой
разрыва II
рода.
Пример
1. Исследовать
функцию
![]() на непрерывность.
на непрерывность.
Решение.
Данная
функция не определена в точках
![]() и
и
![]()
![]() функция имеет разрывы в точках
функция имеет разрывы в точках
![]() .
Чтобы определить тип разрыва, вычислим
односторонние пределы в этих точках.
.
Чтобы определить тип разрыва, вычислим
односторонние пределы в этих точках.
![]() :
:
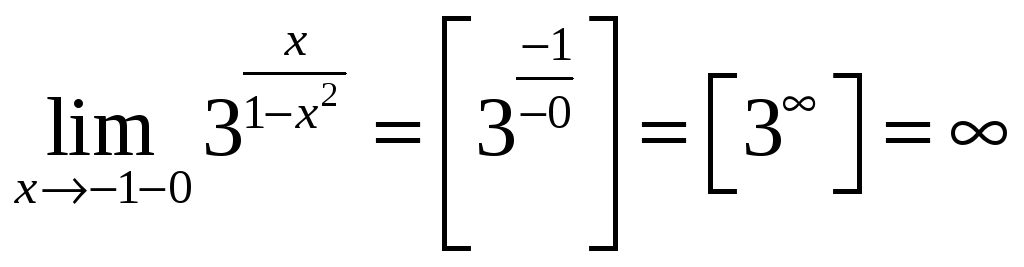 .
.
 .
.
Левосторонний
предел при
![]() равен ∞
равен ∞
![]() данная
точка является точкой разрыва второго
рода.
данная
точка является точкой разрыва второго
рода.
![]() :
:  .
.
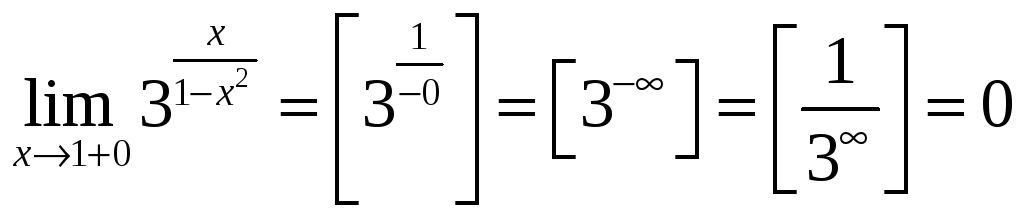 .
.
Левосторонний
предел при
![]() равен ∞
равен ∞
![]() данная
точка является точкой разрыва второго
рода.
данная
точка является точкой разрыва второго
рода.
Пример
2. Исследовать
функцию
![]() на непрерывность.
на непрерывность.
Решение.
Данная
функция не определена при
![]() .
.
При
![]() :
:  .
.
При
![]() :
: 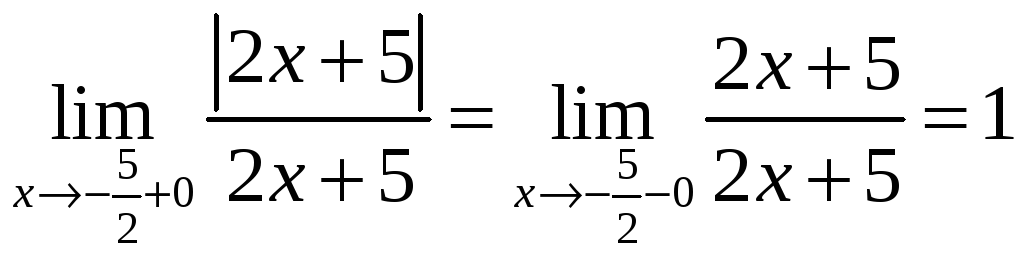 .
.
Значения
односторонних пределов конечны, но не
равны между собой, следовательно, в
точке
![]() существует неустранимый разрыв I
рода.
существует неустранимый разрыв I
рода.
Задания для самостоятельного решения
Вычислить пределы:
1.
![]() 2.
2.
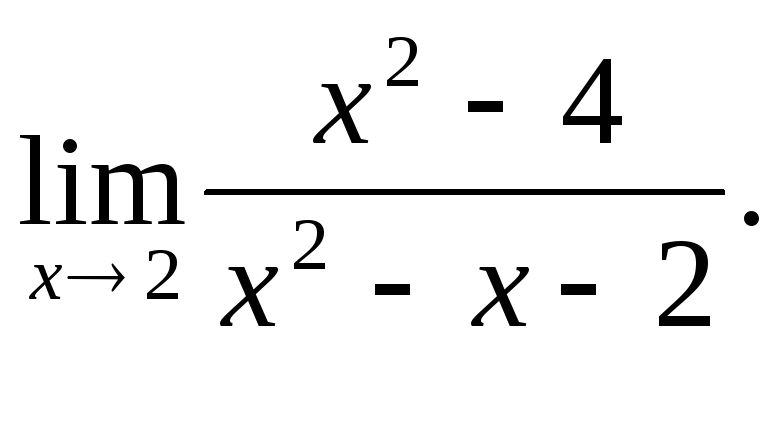 3.
3.
![]()
4.
![]() 5.
5.
![]() 6.
6.
![]()
7.
![]() 8.
8.
![]() 9.
9.
![]()
10.
![]() 11.
11.
![]() 12.
12.
![]()
13.
![]()
Исследовать функцию на непрерывность, указать характер точек разрыва:
14.
![]() . 15.
. 15.
![]() 16.
16.
![]()