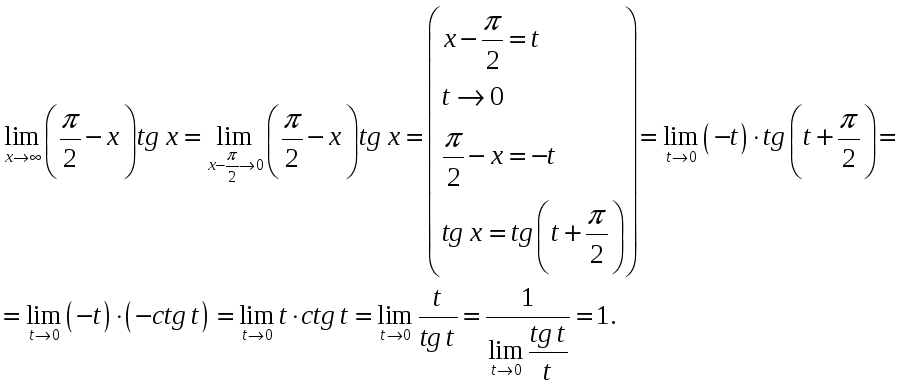- •Комплексные числа
- •Операции над комплексными числами
- •2. Числовые последовательности
- •3. Понятие функции. Предел и непрерывность функции
- •Методы раскрытия неопределённостей при вычислении пределов функций
- •Эквивалентные бесконечно малые величины
- •Непрерывность функции. Классификация точек разрыва
- •Классификация точек разрыва
- •4. Производная и дифференциал функции
- •Правила дифференцирования
- •Дифференциал функции
- •Производные высших порядков
- •Применение производной в экономике. Эластичность функции
- •5. Применение производной к исследованию функций Возрастание и убывание функций. Локальный экстремум функции
- •Наибольшее и наименьшее значения функции
- •Правила Лопиталя для раскрытия неопределенностей
- •Выпуклость, вогнутость и точки перегиба графика функции
- •Асимптоты графика функции
- •Исследование функций и построение графиков
- •Примерные варианты контрольной работы № 1 по математическому анализу
- •6. Неопределённый интеграл Первообразная. Неопределённый интеграл
- •Основные методы интегрирования Метод разложения
- •Метод замены переменной. Подведение под знак дифференциала
- •Метод интегрирования по частям
- •Интегрирование дробно-рациональных выражений
- •Метод неопределённых коэффициентов
- •Интегрирование иррациональных функций
- •Интегрирование тригонометрических функций
3. Понятие функции. Предел и непрерывность функции
Если
определенному элементу х
из множества Х
ставится в соответствие определенный
элемент y
из множества Y,
то говорят, что на множестве Х
задана функция
![]() .
.
При этом величина y называется зависимой переменной, а x- независимой переменной или аргументом. Множество Х называют областью определения функции и обозначают D(f) = X, а множество Y чисел y = f(x) называют множеством значений функции и обозначают E(f) = Y.
Функция называется четной, если она определена на симметричном относительно начала координат промежутке и выполняется f(-x) = f(x), и нечетной, если f(-x) = -f(x).
Функция
называется периодической
с периодом T,
если f(x)
= f(x
+ Tn),
![]()
Пусть
заданы функции y
= f(u)
на U
и u
= g(x)
на X.
Их композицией
(или сложной
функцией,
полученной последовательным применением
функций g
и f)
называется функция y
= f(g(x)),
![]()
Пусть
функция y
= f(x)
определена в окрестности точки
![]() кроме, быть может, самой этой точки.
Число а
называется пределом
функции f(x)
в точке
кроме, быть может, самой этой точки.
Число а
называется пределом
функции f(x)
в точке
![]() (или при
(или при
![]() если
для любого числа
если
для любого числа
![]() найдется число
найдется число
![]() такое, что для всех
такое, что для всех
![]() удовлетворяющих неравенству
удовлетворяющих неравенству
![]() выполняется неравенство
выполняется неравенство
![]()
Обозначается:
![]()
Пример
1. Найти
односторонние пределы функции
![]() в точке
в точке
![]() .
.
Решение.
Вычислим пределы функции в точке
![]() слева и справа, т.е.
слева и справа, т.е.
![]() и
и
![]() .
.
При
![]() :
:
![]() .
.
При
![]() :
:
![]() .
.
Пример
2. Найти
односторонние пределы функции
![]() в точке
в точке
![]() .
.
Решение.
Вычислим пределы
![]() и
и
![]() .
.
При
![]() :
:
![]() -
под знаком квадратного корня отрицательное
число
-
под знаком квадратного корня отрицательное
число
![]() левосторонний предел
левосторонний предел
![]() не существует.
не существует.
При
![]() :
:
![]() .
.
Методы раскрытия неопределённостей при вычислении пределов функций
● Неопределённость
![]() .
.
Примеры:
1.
Вычислить
![]()
Решение.
Для раскрытия неопределенности
![]() разложим числитель и знаменатель на
множители и сократим дробь на (x
– 1). Сокращение
возможно, так как при
разложим числитель и знаменатель на
множители и сократим дробь на (x
– 1). Сокращение
возможно, так как при
![]()
![]() но
но
![]()
![]()
2.
Вычислить
![]()
Решение.
Для раскрытия
неопределенности
![]() преобразуем дробь так, чтобы сократить
её на множитель, стремящийся к нулю (на
x).
Для этого уничтожим иррациональность
в числителе, умножая числитель и
знаменатель на выражение
преобразуем дробь так, чтобы сократить
её на множитель, стремящийся к нулю (на
x).
Для этого уничтожим иррациональность
в числителе, умножая числитель и
знаменатель на выражение
![]() ,
сопряжённое с числителем. Затем сокращаем
дробь на x:
,
сопряжённое с числителем. Затем сокращаем
дробь на x:
![]()
![]()
● Неопределённость
![]() .
.
Примеры:
1.
Вычислить:
![]()
Решение.
Имеем
неопределенность вида
![]() .
Разделив числитель и знаменатель дроби
на
.
Разделив числитель и знаменатель дроби
на
![]() ,
(
,
(![]() -
наибольшая степень переменной х),
получим:
-
наибольшая степень переменной х),
получим:
 .
.
Так как выражение в числителе стремится к 1, а знаменатель – бесконечно малая величина, значит, их отношение есть величина бесконечно большая.
Если
требуется вычислить предел отношения
двух многочленов
![]() ,
где n
– максимальная степень числителя, m
– максимальная степень знаменателя, и
при этом возникает неопределённость
,
где n
– максимальная степень числителя, m
– максимальная степень знаменателя, и
при этом возникает неопределённость
![]() ,
то:
,
то:
-
предел равен 0, если n < m;
-
предел равен ∞, если n > m;
-
предел отношению коэффициентов при максимальных степенях числителя и знаменателя
 ,
если n
= m.
,
если n
= m.
2.
Вычислить
![]() .
.
Решение.
При вычислении возникает неопределённость
![]() ,
максимальная степень числителя n
= 10, максимальная степень знаменателя
m
= 10, следовательно
предел равен отношению коэффициентов,
стоящих при этих степенях:
,
максимальная степень числителя n
= 10, максимальная степень знаменателя
m
= 10, следовательно
предел равен отношению коэффициентов,
стоящих при этих степенях:
![]() .
.
3.
Вычислить
![]() .
.
Решение.
![]() ,
,
![]() ,
n
> m
,
n
> m
![]() .
.
4.
Вычислить
![]() .
.
Решение.
![]() ,
,
![]() ,
n
< m
,
n
< m
![]() .
.
● Неопределённость
![]() .
.
Примеры:
1.
Вычислить
![]()
Решение.
Имеем неопределённость вида
![]() ,так
как
,так
как
![]() ,
,
![]()
Воспользуемся
вторым замечательным пределом. Представим
дробь в виде суммы 1 и бесконечно малой
функции:
![]()

2.
Вычислить
 .
.
Решение.
Воспользуемся формулой следствия из
второго замечательного предела
![]() :
:
 .
.
3.
Вычислить
![]() .
.
Решение.
Воспользуемся формулой следствия из
второго замечательного предела
![]() :
:
 .
.
● Неопределённость
![]() .
.
Примеры:
1.
Вычислить
![]() .
.
Решение.
![]()
2.
Вычислить
![]() .
.
Решение. Умножим и разделим данное выражение на сопряжённое:

● Неопределённость
![]() .
.
Примеры:
1.
Вычислить
![]() .
.
Решение.
Представим переменную х
как
![]() и воспользуемся первым замечательным
пределом, заменив
и воспользуемся первым замечательным
пределом, заменив
![]() на новую переменную t:
на новую переменную t:
 .
.
2.
Вычислить
 .
.
Решение.
Так как
![]() ,
то
,
то
![]() .
Заменим
.
Заменим
![]() на новую переменную и воспользуемся
следствием из первого замечательного
предела
на новую переменную и воспользуемся
следствием из первого замечательного
предела
![]() :
: