Множественный линейный регрессионный анализ

Экономические явления обычно определяются большим числом одновременно и совокупно действующих факторов. В связи с чем часто возникает задача исследования зависимости объясняемой переменной y от нескольких объясняющих переменных х₁, х₂, х₃, …, х_р. Эта задача решается с помощью множественного регрессионного анализа.

Предположим, что по генеральной совокупности между объясняемой переменной y и совокупностью P-объясняющих переменных существует гипотетическая линейная зависимость

(25)

И по выборке из n-наблюдений (y_i, x_i1, x_i2,…,x_ip) i = 1,…, n будем строить аппроксимирующую зависимость:

(26)

В дальнейшем мы предположим, что спецификация модели (26) правильная (т.е. вид модели выбран правильно и в нее включены только те объясняющие переменные, которые в нее должны входить). Также будем полагать, что для случайной величины ε, участвующей в зависимости (25), справедливы условия Гаусса – Маркова 1 – 4 и вдобавок к ним справедливо еще 5 – ое [4]: объясняющие переменные х₁, х₂, х₃, …, х_р линейно независимы.

Параметры b₀, b₁, b₂, …, b_{p ,} входящие в модель (26) будем определять методом наименьших квадратов, т.е. исходя из условия:

(27)

Из необходимого условия экстремума функции многих переменных имеем:

(28)

После преобразования системы уравнений (28) и записи ее в более привычной форме, она примет вид:

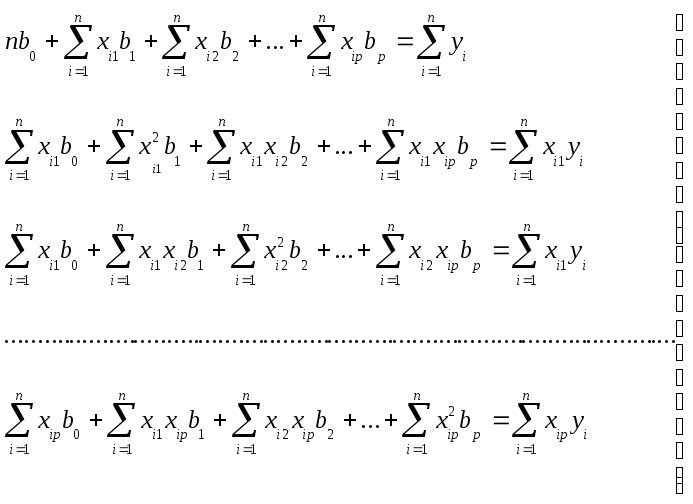(29)

Система (29) представляет собой систему линейных алгебраических уравнений состоящую из р + 1 уравнения с р + 1 одним неизвестным. Решив эту систему одним из известных методов, например Гаусса или Гаусса - Жордана, найдем значения параметров b₀, b₁, b₂,…, b_p и тем самым построим модель (26) наилучшим образом аппроксимирующую искомую модель (25) в смысле наименьших квадратов.

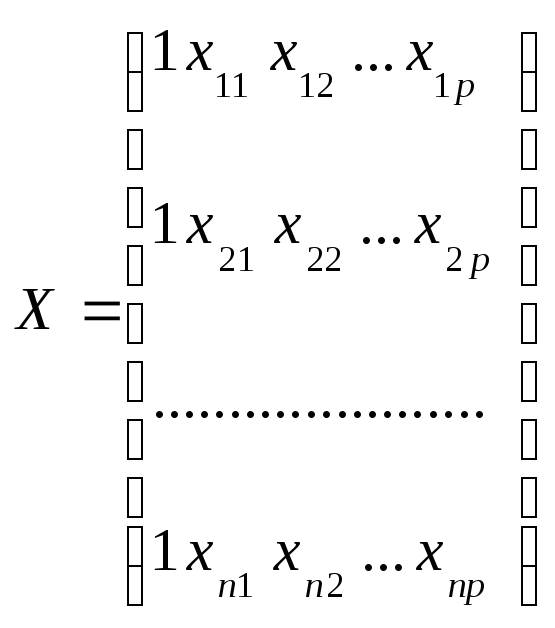
Для того, чтобы система (29) имела единственное решение, т.е. матрица ее коэффициентов была невырожденной должно выполняться условие линейной независимости столбцов матрицы:

, (30)

матрицы значений объясняющих переменных в выборке наблюдений, по которой строится модель (26). Выполнение этого условия гарантируется выполнением 5 – го условия Гаусса – Маркова. Кроме этого полагают, что число имеющихся наблюдений каждой из объясняющих и объясняемой переменных превосходит ранг матрицы X, т.е. n > p + 1, потому что в противном случае в принципе невозможно получение сколько-нибудь надежных статистических выводов.

Решение системы линейных алгебраических уравнений (29) а также выполнение дальнейшего статистического анализа построенной модели (26) при p > 2 является очень трудоемкой задачей и для его реализации нужно использовать специальные пакеты прикладных программ, например MS – Excel, или ППП Statistika 5.0.

Рассмотрим как решается задача построения уравнения линейной множественной регрессии при р = 2, т.е. в случае когда модель (25) приобретает вид:

, (31)

а модель (26) имеет вид:

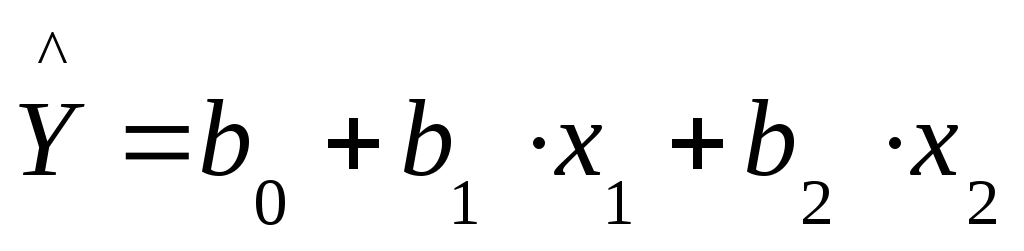(32)

Для определения значений параметров b₀, b₁, b₂ по выборке объема n по методу наименьших квадратов получаем следующую систему:

(33)

Первое уравнение системы (33) можно записать в виде:

(34)

После подстановки выражения для b₀ в два оставшихся уравнения системы (33) они приобретают вид:

или

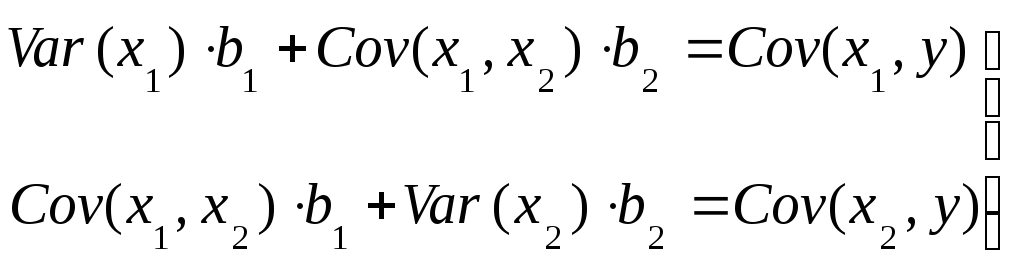(35)

Решив систему (35) методом, например, подстановок получаем следующие выражения для b₁ и b₂:

; (36)

. (37)

Статистический анализ построенной модели производится так же как и в случае парной линейной регрессии.

Вначале покажем, что коэффициенты b₀, b₁, b₂ являются несмещенными оценками параметров β₀, β₁, β₂. Несмещенность оценок покажем на примере коэффициента b₁. Из формулы (36) имеем:

(38)

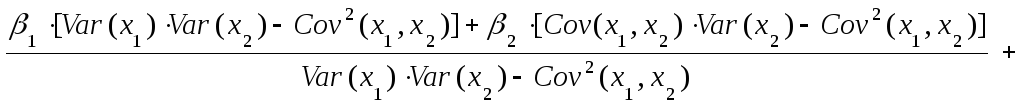
Из (38) видно, что значение коэффициента b₁ определяется неслучайной составляющей β₁ и случайной составляющей, определяемой выражением:

.

Теперь покажем, что математическое ожидание b₁ равняется β₁:

(39)

Совершенно аналогично можно показать, что М(b₀) = β₀, М(b₂) = β₂

Далее найдем дисперсии коэффициентов. Сначала это сделаем для коэффициента b₁:

)

С учетом формулы (39) имеем:

(40)

Формула для дисперсии коэффициента b₂ получается из формулы (40) путем замены характеристик х₁ на соответствующие характеристики х₂, т.е. она имеет вид:

(41)

После проведения аналогичных выкладок для дисперсии коэффициента b₀ получаем следующую формулу:

(42)

Как видно из формул (40) – (42) коэффициенты регрессии b₀, b₁, b₂ являются более точными:

а) чем больше число наблюдений в выборке;

б) чем больше дисперсии объясняющих переменных в выборке;

в) чем меньше теоретическая дисперсия случайного члена;

г) чем меньше связаны между собой объясняющие переменные.

Первые три из желательных условий повторяют те, которые были справедливы и для случая парной регрессии. Лишь четвертое условие является новым. Из этого условия следует, что желательно иметь как можно более слабую корреляцию между х₁ и х_2.

Стандартная ошибка коэффициента множественной регрессии имеет такой же смысл, как и в парном регрессионном анализе. Как и в парном регрессионном анализе, формула для стандартной ошибки коэффициента регрессии может быть выведена на основе формулы дисперсии коэффициента регрессии путем замены дисперсии случайного члена σ² на ее несмещенную оценку и извлечения квадратного корня.

Несмещенной оценкой σ² является величина S² (остаточная дисперсия):

(43)

С учетом соотношений (40) –(43) стандартные ошибки коэффициентов регрессии b₀, b₁, b₂ будут определяться по следующим формулам:

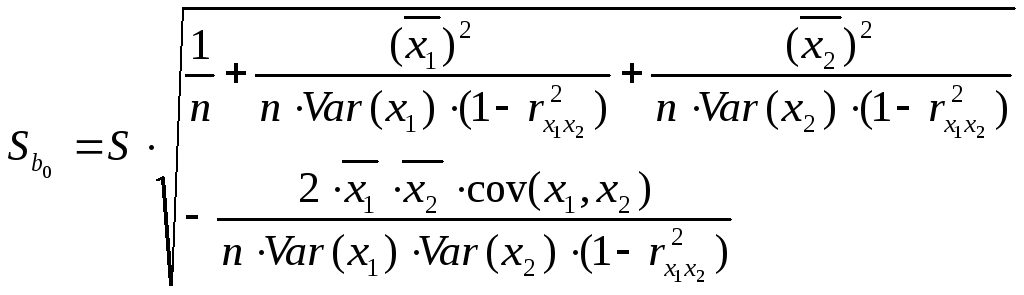, (44)

, (45)

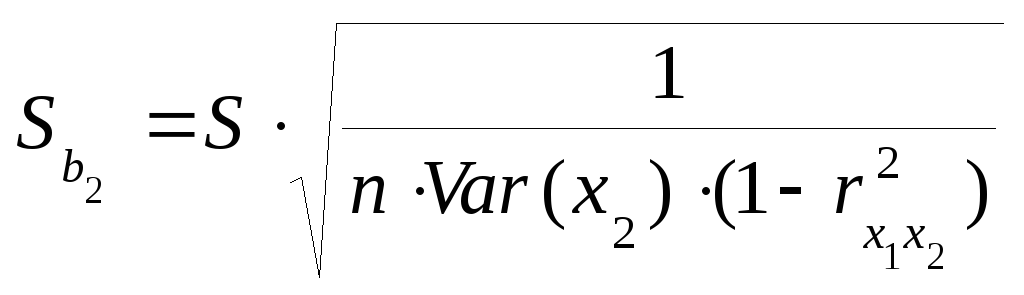. (46)

t - тесты для коэффициентов множественной линейной регрессии реализуются так же как это делается в парном регрессионном анализе. Отметим, что критический уровень t при любом уровне значимости зависит от числа степеней свободы, которое равно (n-k-1): где n – число наблюдений в выборке, k – число объясняющих переменных. Доверительные интервалы определяются точно так же, как и в парном регрессионном анализе в соответствии с указанным примечанием относительно числа степеней свободы.

Как и в парном регрессионном анализе, коэффициент детерминации R² определяет долю дисперсии y объясненную регрессией и вычисляется по формуле:

Коэффициент R² никогда не уменьшается (а обычно увеличивается) при добавлении еще одной объясняющей переменной в уравнение регрессии, если все ранее включенные объясняющие переменные сохраняются в уравнении. Для компенсации такого увеличения R² вводится скорректированный коэффициент детерминации с поправкой на число степеней свободы:

(47)

Если увеличение доли разброса объясняемой переменной y, объясненной регрессией при добавлении новой переменной мало, то скорректированный коэффициент детерминации может уменьшиться, следовательно, добавлять новую объясняющую переменную в уравнение регрессии нецелесообразно.

Кроме того, если объясняющие переменные х₁ и х₂ сильно коррелированы между собой, то они объясняют одну и ту же часть разброса переменной у, поэтому в этом случае трудно оценить вклад каждой из переменных в объяснении поведения у.

Для проверки адекватности построенного уравнения регрессии используется F – критерий. Для этого выдвигаем нулевую гипотезу H₀: F = 0, затем вычисляем статистику:

, (48)

здесь k = 2 – число объясняющих переменных в уравнении регрессии.

Статистика F подчиняется распределению Фишера – Снедекора. В таблице распределения критерия Фишера - Снедекора находим для заданного уровня значимости α и числа степеней свободы k₁ = k и k₂ = n – k - 1 критическое значение F_кр= F(α, k₁, k₂). Если F < F_кр у нас нет оснований отвергнуть гипотезу H₀, если же F > F_кр мы отвергаем нулевую гипотезу H₀ и признаем, что построенное уравнение регрессии адекватно описывает наблюдаемые в выборке значения объясняемой переменной у и им можно пользоваться для прогнозирования значений у при соответствующих значениях объясняющих переменных.

Применение изложенной теории рассмотрим на примере решения следующей задачи: изучается зависимость между сменной добычей торфа на одного работающего y(т), мощностью пласта x₁(м) и уровнем механизации работ x₂(%) по следующим (условным) данным, характеризующим процесс добычи торфа в n = 10 карьерах. Данные приведены в таблице 3.

Таблица 3

I	1	2	3	4	5	6	7	8	9	10
Xi1	4	11	14	9	8	8	15	9	8	12
Xi2	30	70	50	40	20	60	100	10	50	40
yi	2	8	10	6	4	5	12	4	5	9

Предположим, что между объясняемой переменной y и объясняющими переменными x₁ и x₂ существует линейная зависимость:

. (49)

По имеющейся у нас выборке наблюдений методом наименьших квадратов построим зависимость:

. (50)

Будем предполагать, что все условия Гаусса – Маркова для случайного члена в зависимости (49) выполнены.

Для удобства и повышения наглядности расчетов составим вспомогательную таблицу 4:

Теперь по ранее полученным формулам вычисляем значения величин:

;

;

;

;

Таблица 4

№	x1	x2	y	x12	x22	y2
1 2 3 4 5 6 7 8 9 10	4 11 14 9 8 8 15 9 8 12	30 70 50 40 20 60 100 10 50 40	2 8 10 6 4 5 12 4 5 9	16 121 196 81 64 64 225 81 64 144	900 4900 2500 1600 400 3600 10000 100 2500 1600	4 64 100 36 16 25 144 16 25 81	98,600 27,600 12,600 5,600 48,600 -23,400 275,600 29,600 -5,400 -15,400	26,100 1,800 14,700 0,400 4,500 2,700 28,600 2,000 2,700 5,500
∑	98	470	65	1056	28100	511	454,000	89,000
Среднее значение	9,8	47	6,5	105,6	2810	51,1	45,400	8,900

Продолжение таблицы 4

№					Аi
1 2 3 4 5 6 7 8 9 10	76,500 34,500 10,500 3,500 67,500 -19,500 291,500 92,500 -4,500 -17,500	1,408 8,121 9,916 5,662 4,286 5,452 12,166 4,787 5,161 8,040	0,351 0,015 0,007 0,114 0,082 0,205 0,028 0,600 0,026 0,923	20,250 0,250 12,250 0,250 6,250 2,250 30,250 6,250 2,250 6,250	29,750 1,450 0,850 5,667 7,175 8,940 1,317 19,750 3,140 10,678
∑	535,000		0,370	88,500	88,720
Среднее значение	53,500		0,237	8,850	8,872

;

;

;

;

;

;

;

;

;

;

;

;

;

;

Далее задаемся уровнем значимости α = 0,05; вычисляем число степеней свободы по формуле v = n – k – 1 = 10 – 2 – 1 = 7 и по таблице распределения критерия Стьюдента определяем t_кр = t(0,05; 7) = 2,360; выдвигаем гипотезу H₀: β₀ = 0, так как t_b0 = 5,201 > t_кр = 2,360, то гипотезу H₀ отвергаем и поэтому делаем заключение что β₀ значимо отличается от 0. Аналогичные заключения делаем и по коэффициентам β₁ и β₂ так как справедливы неравенства: t_b1= 10,716 > t_кр = 2,360 и t_b2 = 3,222 > tкр = 2,360.

Теперь проверим адекватность построенного уравнения регрессии наблюдаемым значениям объясняемой переменной y. Для этого вычислим статистику F:

.

Выдвигаем нулевую гипотезу Н₀: F = 0 Для уровня значимости α = 0,05 числа степеней k₁ = k = 2 и k₂ = n – k – 1 = 10 – 2 – 1 = 7 по таблице распределения критерия Фишера - Снедекора определяем F_кр = F(0,05; 2, 7) = 4,740 так как F=117,018 > F_кр = 4,740 нулевую гипотезу Н₀: F = 0 отвергаем и признаем, что построенное уравнение регрессии адекватно описывает наблюдаемые в выборке значения объясняемой переменной у.

Таким образом, построенное уравнение регрессии имеет вид:

. (51)

Оно показывает, что увеличение только мощности пласта торфа x₁ (при неизменном x₂) на 1 метр приводит к увеличению добычи торфа на одного рабочего в среднем на 0,793 тонны; а увеличение только уровня механизации x₂ (при неизменном x₁) на 1% приводит к увеличению добычи торфа на одного рабочего в среднем на 0,029 т. Коэффициент b₀ = -2.637, в данном случае, ясного экономического смысла не имеет.