Министерство сельского хозяйства Российской Федерации

Федеральное государственное образовательное учреждение

высшего профессионального образования

Казанский государственный аграрный университет

Кафедра экономической кибернетики

Методическое пособие по курсу «Эконометрика»

Казань

2006

УДК 518.7

ББК: у050.030.4

Методическое пособие предназначено для обучения студентов практическим приемам реализации регрессионного анализа при изучении основ курса «Эконометрика».

Методическое пособие разработано доцентом кафедры экономической кибернетики, к.т.н. Гильфановым Р.М.

Методическое пособие обсуждено на заседании кафедры (протокол № 4 от 24.11.2006 г.) и утверждено на заседании учебно-методической комиссией института экономики (протокол № 4 от 11.12.2006 г.)

Рецензенты: к.э.н., доцент, зав. кафедрой бухгалтерского учета КГАУ

Мухаметзянов К.З.

к. ф. – м. н., доцент кафедры прикладной математики КГАСУ,

Габбасов Ф. Г.

 Казанский государственный аграрный университет, 2006

Введение

В данной работе рассматриваются вопросы построения линейных регрессионных моделей. Регрессионный анализ занимает центральное место в математико-статистическом инструментарии эконометрики. Он представляет собой математический инструментарий для статистического исследования взаимосвязей между изучаемыми экономическими явлениями или показателями.

Линейные зависимости в экономике довольно распространены. Вместе с тем линейные зависимости являются очень простыми и наглядными. Поэтому в работе подробно рассмотрены вопросы построения линейных регрессионных моделей в случае одной объясняющей переменной и в случае двух объясняющих переменных, а так же интерпретации построенных моделей.

Освоение студентами изложенного в работе материала поможет им при изучении других разделов эконометрики.

Модель парной линейной регрессии

Модель парной линейной регрессии включает две переменные y и x. Пусть между ними зависимость в генеральной совокупности представляется в виде

y = α + βּx + ε, (1)

где x – неслучайная величина; y и ε – случайные величины. Величина y – объясняемая переменная, x – объясняющая переменная, α и β – параметры зависимости.

Наличие случайной величины ε в зависимости (1) определяется влиянием на объяснимую переменную y, не включенных в уравнение объясняющих переменных, а так же с возможной нелинейностью модели и ошибками измерения.

Будем полагать, что для случайного члена ε справедливы условия Гаусса – Маркова [1].

1. Математическое ожидание случайного члена ε в любом наблюдении должно быть равно нулю, то есть М(ε_i) = 0, i = .

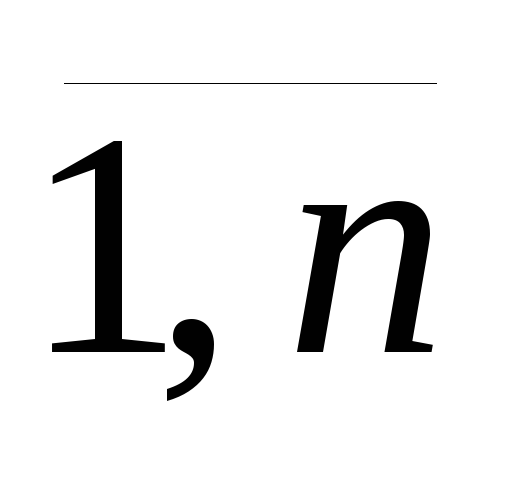2. Дисперсия случайного члена ε должна быть постоянной для всех наблюдений, то есть D(ε_i) = σ², i = .

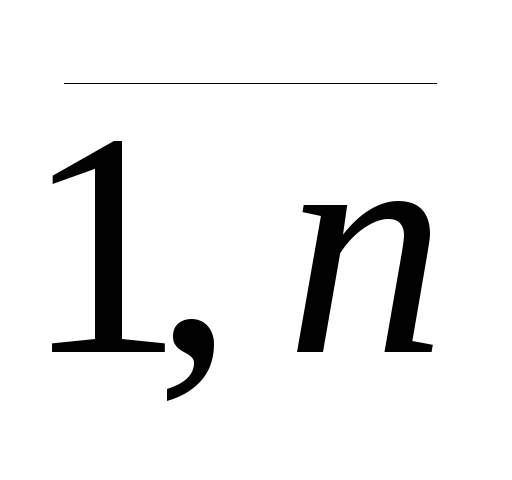3. Значения случайного члена ε в разных наблюдениях ε_i и ε_j (i <>j) должны быть статистически независимы (некоррелированы) между собой то есть M(ε_i ε_j) = 0 ( i <> j ).

4. Объясняющая переменная х неслучайная величина.

Пусть имеется выборка наблюдений (x_i; y_i) i = и на основе этой выборки нужно построить выборочное уравнение регрессии

y = a + bּx, (2)

где a, b – оценки параметров α и β.

Определим остаток e_i в i-ом наблюдении как разность между наблюдаемым и расчетным значениями объясняемой переменной т. е.

e_i = y_i – _i.

Неизвестные значения параметров a и b определим методом наименьших квадратов (МНК).

Суть метода мнк заключается в минимизации суммы квадратов остатков

P = (3)

Для фиксированной выборки наблюдений (x_i, y_i) i = – известные значения наблюдений; a, b – неизвестные.

Записав необходимое условие достижения экстремума функцией P, получаем систему:

Преобразовав эту систему, получим следующую систему нормальных уравнений:

,

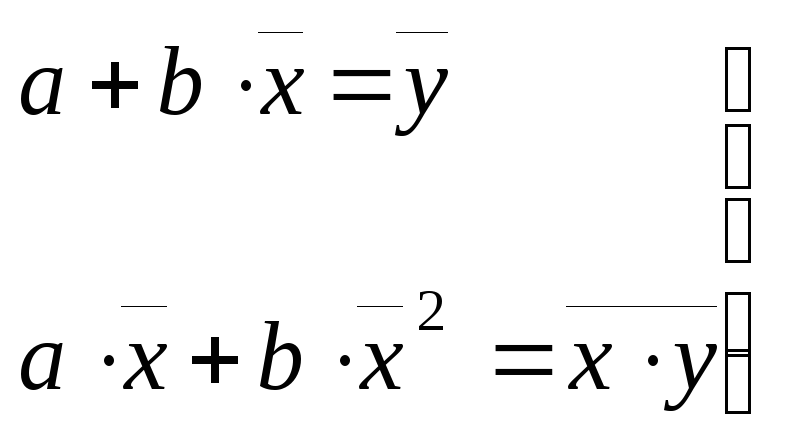здесь и далее в работе знак черточки над соответствующей переменной означает ее среднее значение по выборке наблюдений.

Решив эту систему, например, методом подстановки получаем следующие выражения для коэффициентов a и b:

, (4)

. (5)

Подставив в (2) выражение для a из (5) получим:

(6)

Из (6) следует, что линия регрессии проходит через точку , и выполняются равенства:

Коэффициент b есть угловой коэффициент регрессии, он показывает, на сколько единиц, в среднем, изменяется переменная y при изменении переменной x на единицу.

Коэффициент a дает прогнозируемое значение объясняемой переменной у при x = 0. Это может иметь смысл в зависимости от того, далеко ли находится x = 0 от выборочных значений x.

После построения уравнения регрессии, наблюдаемые значения объясняемой переменной можно представить как:

А так же можно вычислить выборочные дисперсии величин y, y, e:

- дисперсия наблюдаемых значений y ;

- дисперсия расчетных значений :

– дисперсия остатков.

Разброс значений объясняемой переменной характеризуется выборочной дисперсией Var(y). Представим Var(y) следующим образом:

.

Так как

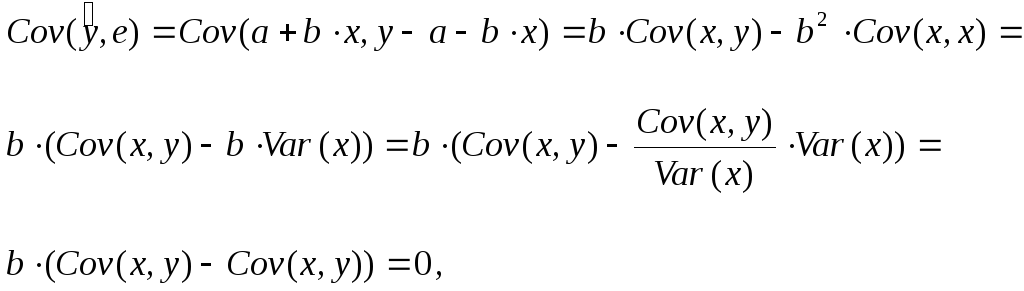
то

(7)

Как видно из формулы (7) дисперсия Var(y) разложена на две составляющие: Var() – часть, объясненную уравнением регрессии; Var(e) – часть, необъясненную уравнением регрессии.

Коэффициентом детерминации R² называется отношение:

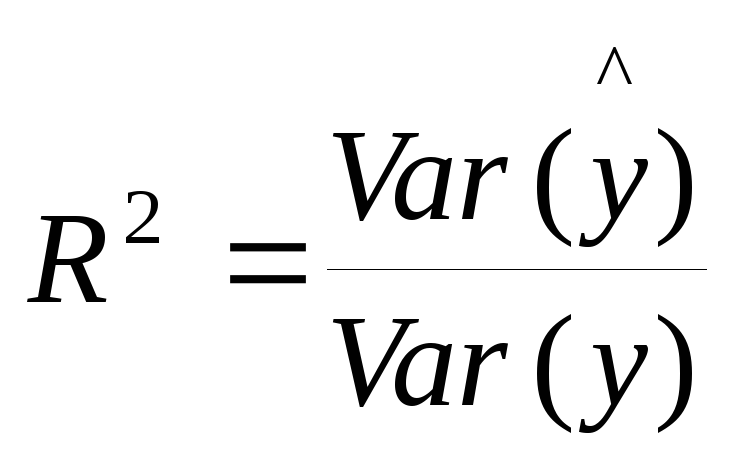(8)

Из формулы (7) можно получить другое выражение для R²:

(9)

Коэффициент детерминации характеризует долю разброса зависимой переменной y, объясненную с помощью уравнения регрессии (2). Отношение Var(e) / Var(y) выражает собой необъясненную уравнением регрессии (2) долю дисперсии y.

Как следует из (8) и (9) 0 ≤ R² ≤ 1. При R² = 1, построенное уравнение регрессии (2) точно описывает наблюдаемые в выборке значения y т. е. y_i = _i i =; так как Var(y) = Var() и Var(e) = 0.

При R² = 0, построенное уравнение регрессии (2) ничего не дает, так как Var(y) = Var(e), Var()= 0, y_i = i =; т. е. качество предсказания у уравнения регрессии (2) ничуть не лучше чем у прямой .

При 0 < R² < 1, чем ближе значение R² к единице, тем лучше качество аппроксимации наблюдаемых значений y.

Для определения статистической значимости коэффициента детерминации R² проверяется гипотеза H₀: F = 0 для F-статистики, рассчитываемой по формуле:

(10)

Величина F имеет распределение Фишера –Снедекора с k₁ = 1, k₂ = n – 2 степенями свободы. Для заданного уровня значимости α (как правило, берется α = 0,05) из таблицы распределения критерия Фишера – Снедекора определяем F_кр = F(α, k₁, k₂). Далее вычисленный по формуле (10) критерий F сравнивается с F_кр, определенным из таблицы:

0. если F < F_кр, то Н₀ принимается, т.е. R² – незначим;

1. если F > F_кр, то Н₀ отклоняется, т. е. R² – значим;

Далее вычисляем дисперсии коэффициентов a, b для того, чтобы затем использовать их для проверки на значимость этих коэффициентов.