7. Теорема Коши.
Теорема Коши. Пусть
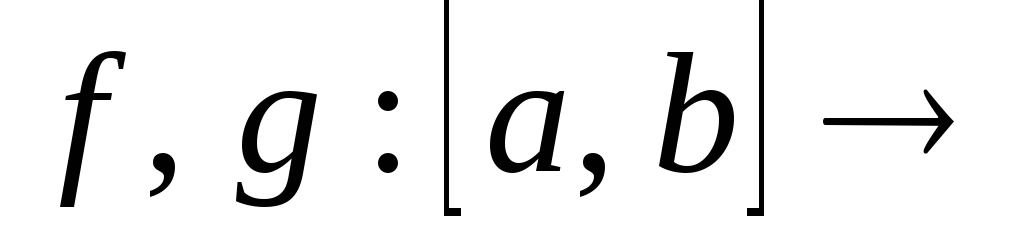 R
– функции непрерывные на
R
– функции непрерывные на
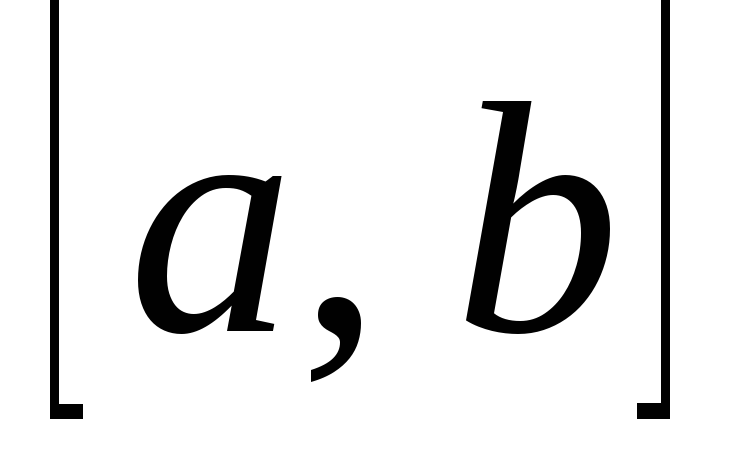 и дифференцируемые на
и дифференцируемые на
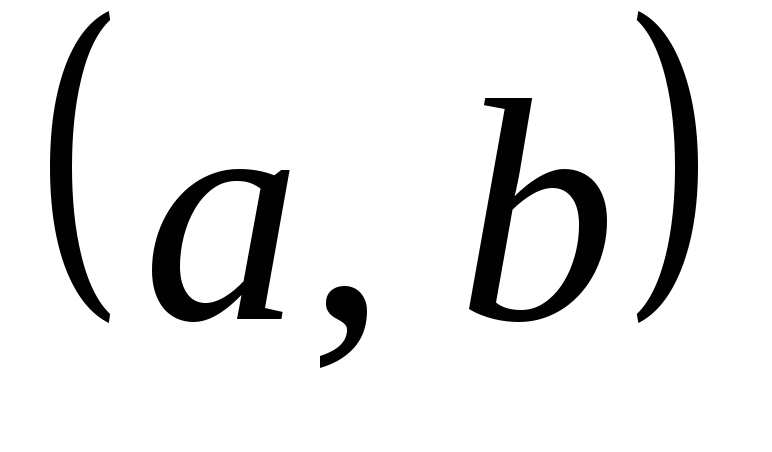 ;
кроме того, пусть
;
кроме того, пусть
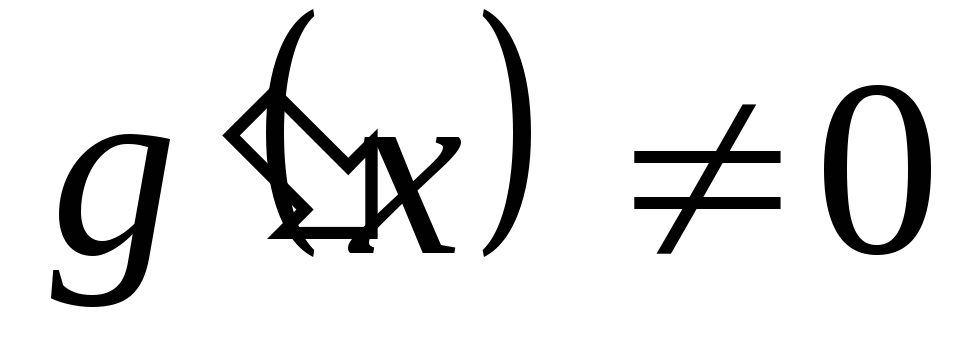 при всех
при всех
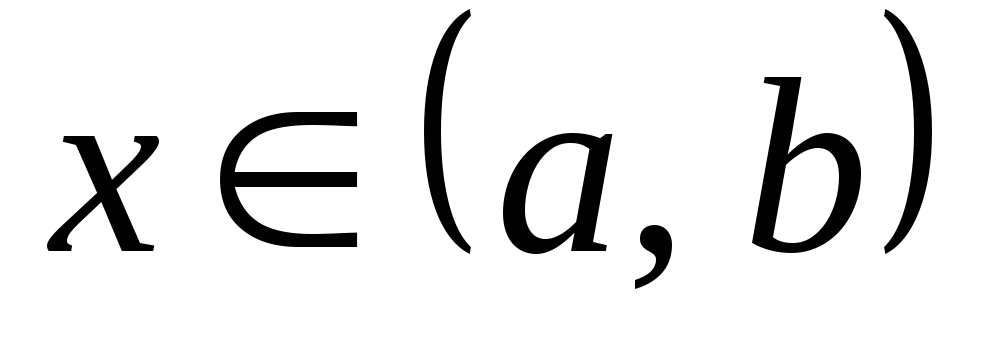 .
Тогда
.
Тогда
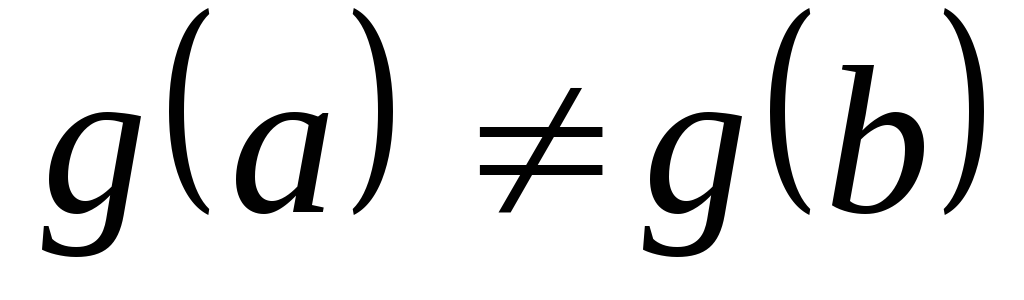 и существует
и существует
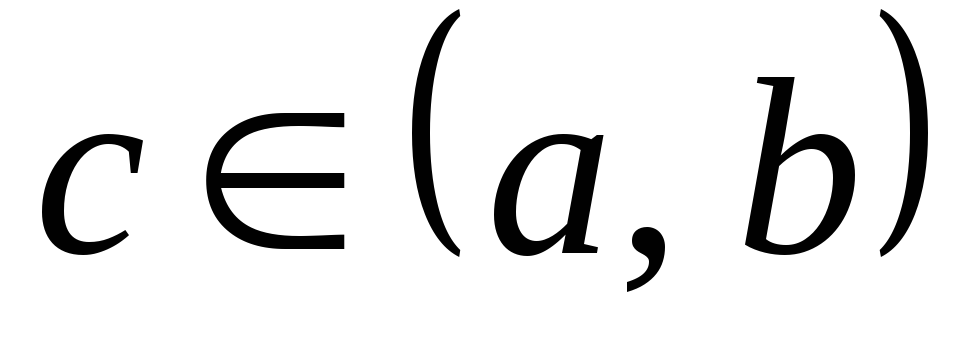 такое, что
такое, что
 .
.
Доказательство.
Поскольку по теореме Лагранжа
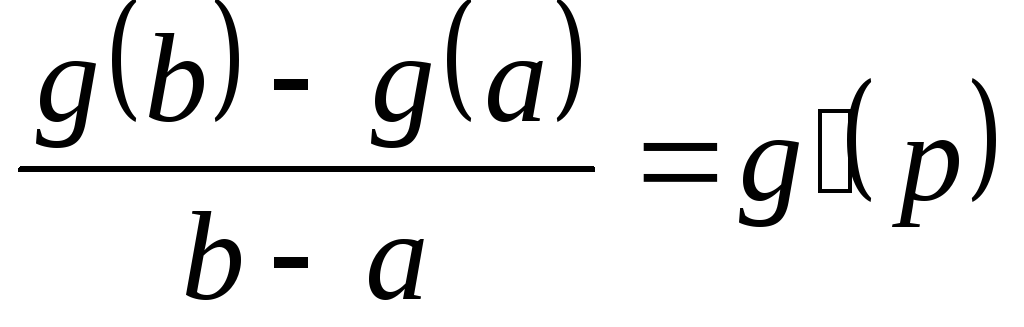 для некоторого
для некоторого
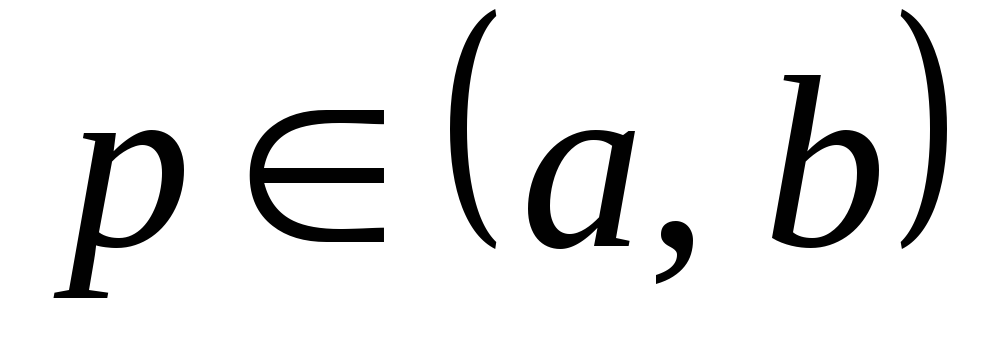 ,
имеем
,
имеем
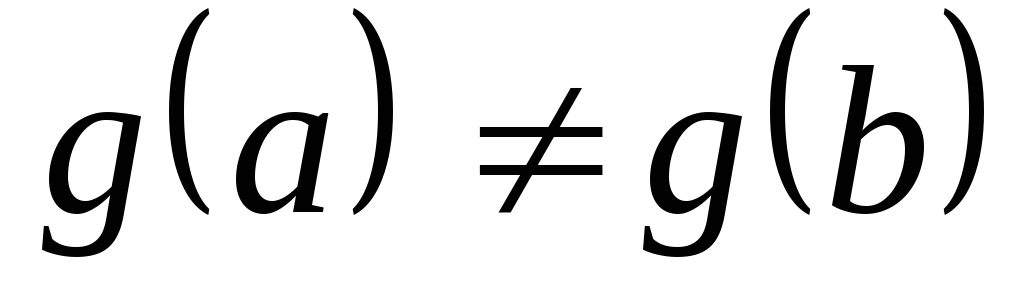 .
Положим
.
Положим
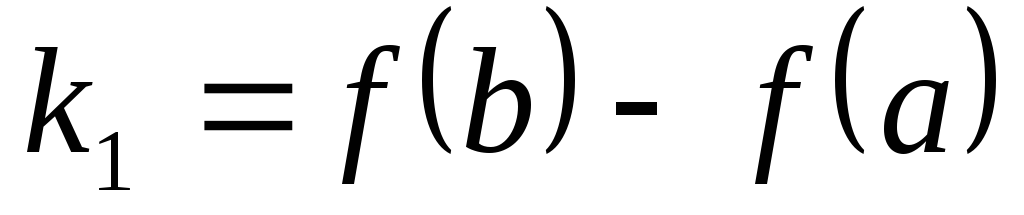 ,
,
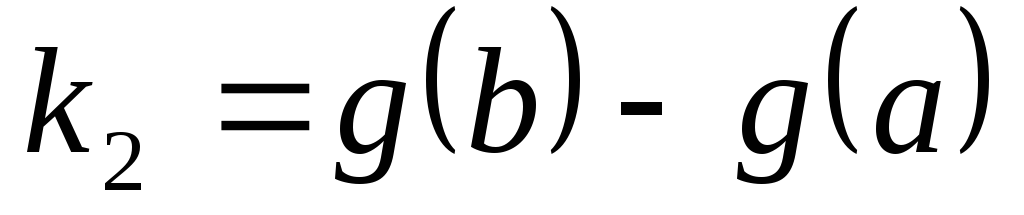 и рассмотрим функцию
и рассмотрим функцию
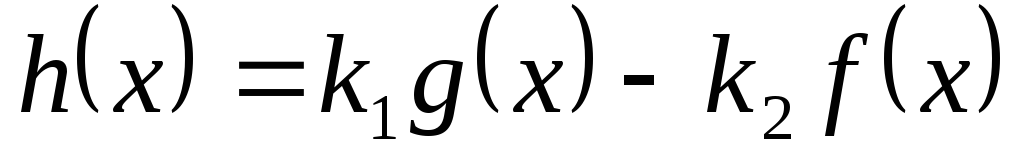 .
Тогда функция
.
Тогда функция
 непрерывна на
непрерывна на
 и дифференцируема на
и дифференцируема на
 ;
кроме того
;
кроме того
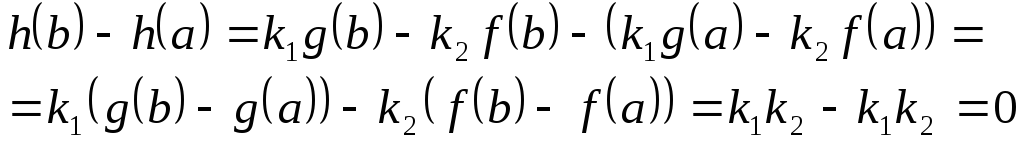
Следовательно,
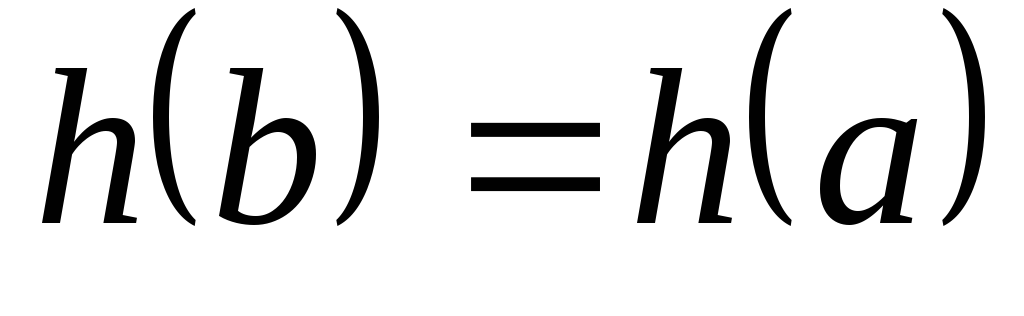 и по теореме Ролля существует
и по теореме Ролля существует
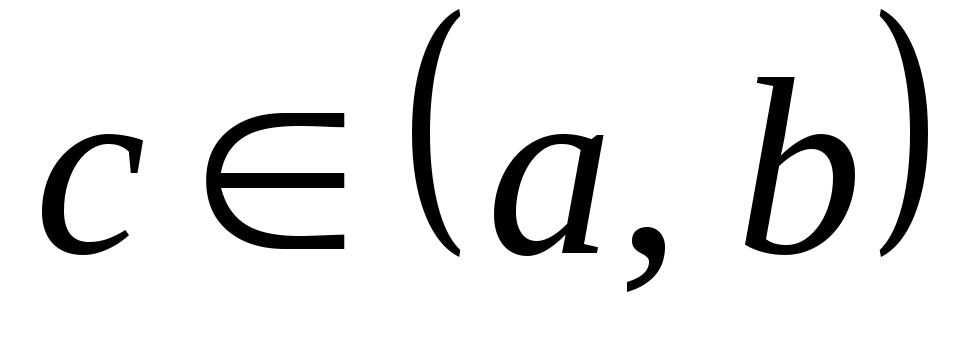 такое, что
такое, что
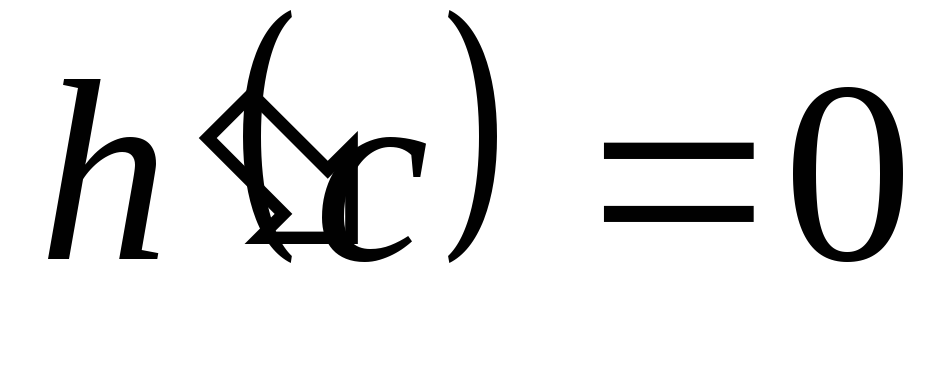 .
Это значит, что
.
Это значит, что
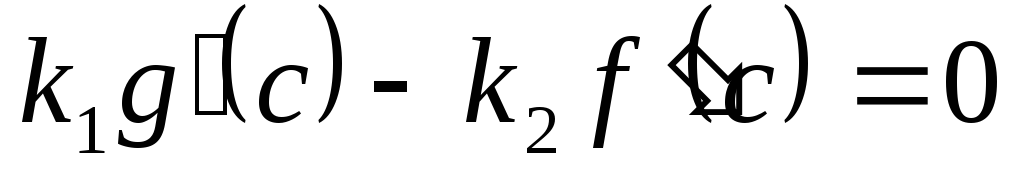 ,
то есть
,
то есть
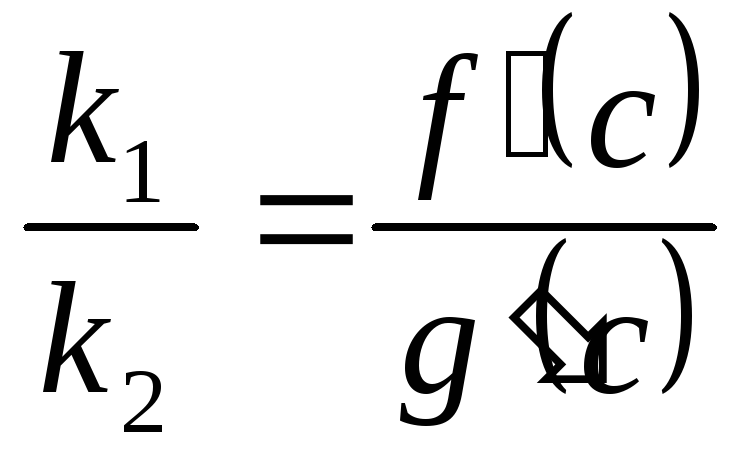 ,
что и требовалось.
,
что и требовалось.
8. Правило Лопиталя.
Теорема. Пусть
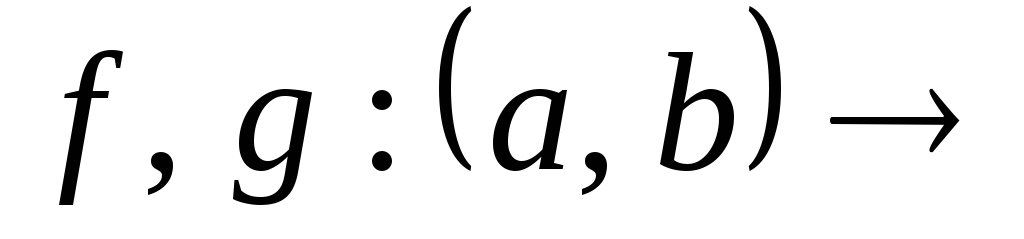 R,
причем функции
R,
причем функции
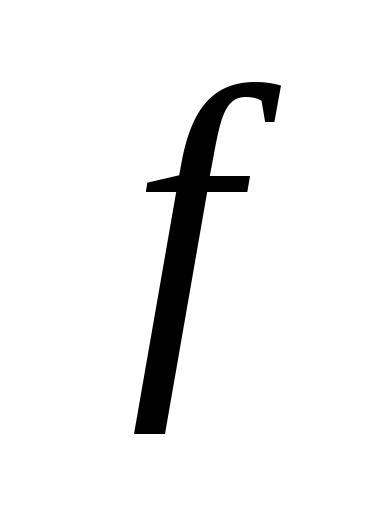 и
и
 дифференцируемы на
дифференцируемы на
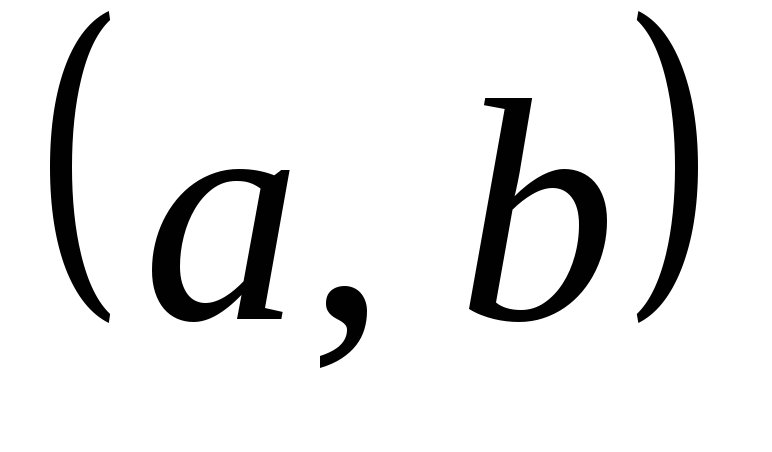 ,
и при любом
,
и при любом
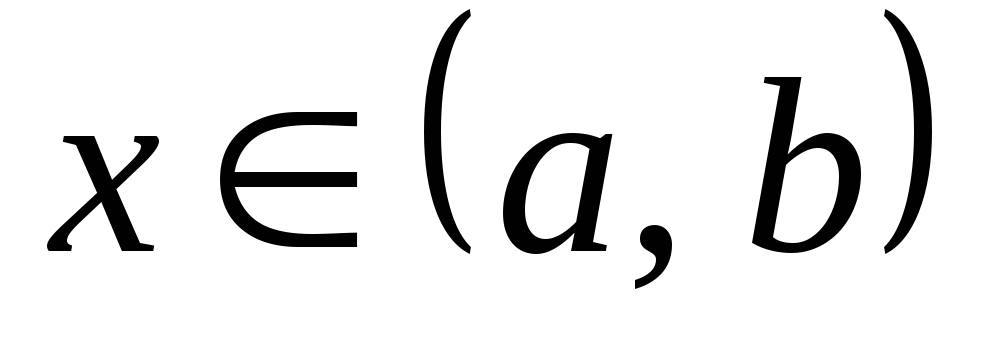
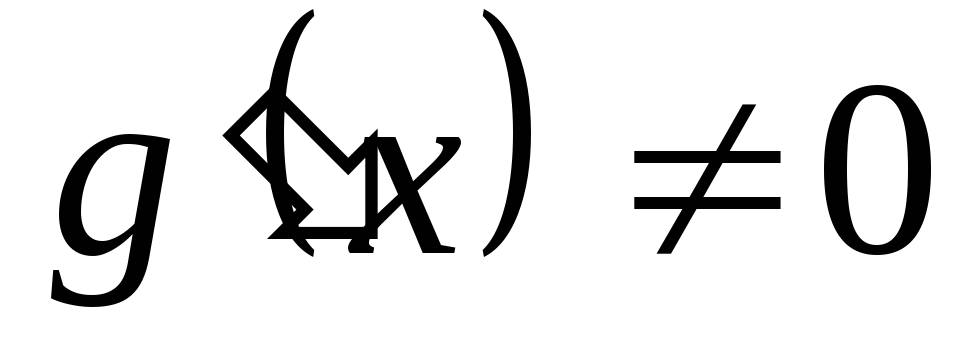 и
и
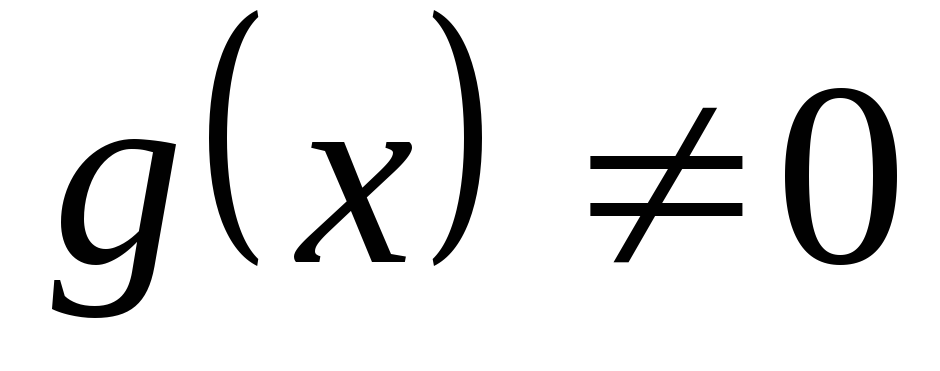 .
Предположим, что существуют пределы
функций
.
Предположим, что существуют пределы
функций
 и
и
 при
при
 ,
причем либо
,
причем либо
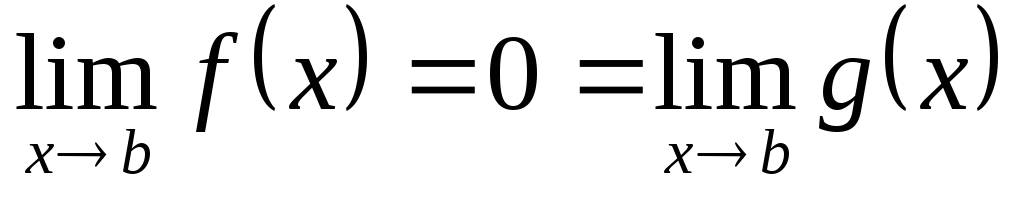 ,
либо
,
либо
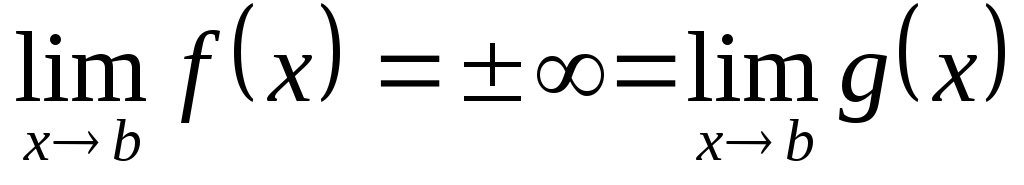 .
.
Тогда
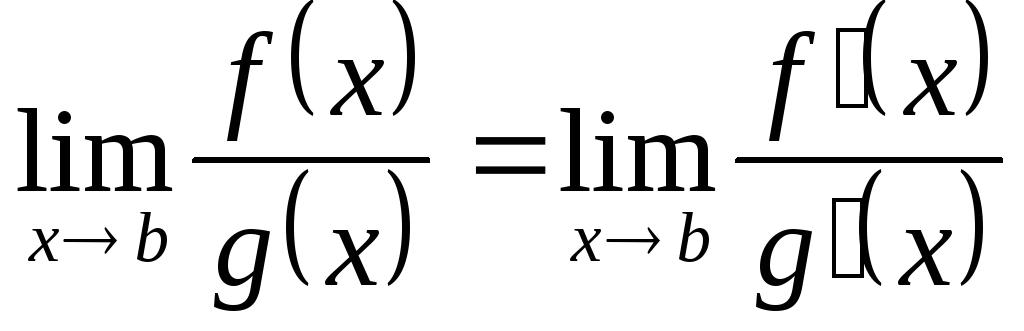 в случае, если последний предел
существует, конечный или бесконечный.
в случае, если последний предел
существует, конечный или бесконечный.
Доказательство.
Мы приведем доказательство теоремы
только при условии, что
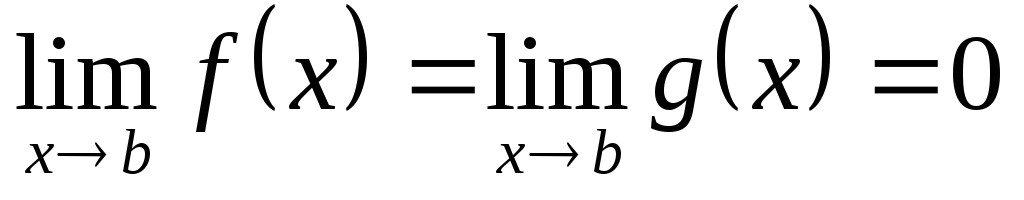 и
и
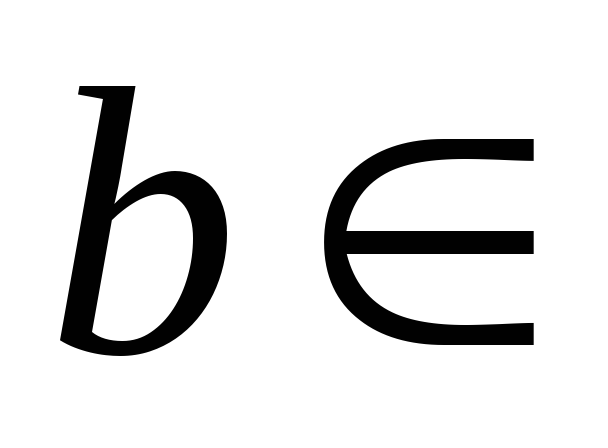 R
(т. е.
R
(т. е.
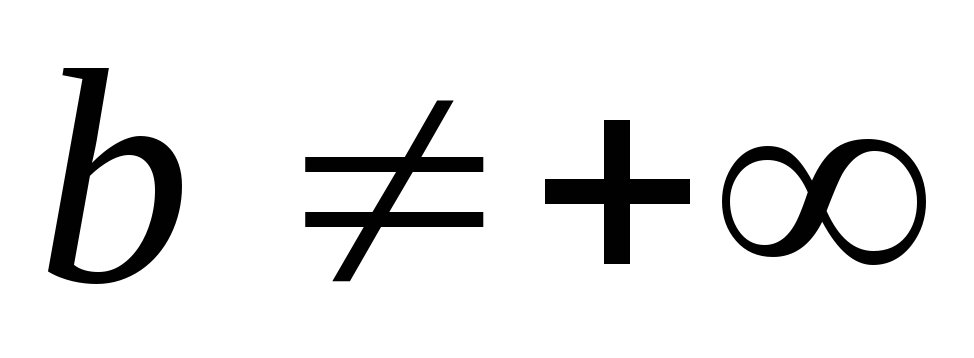 ).
Пусть
).
Пусть
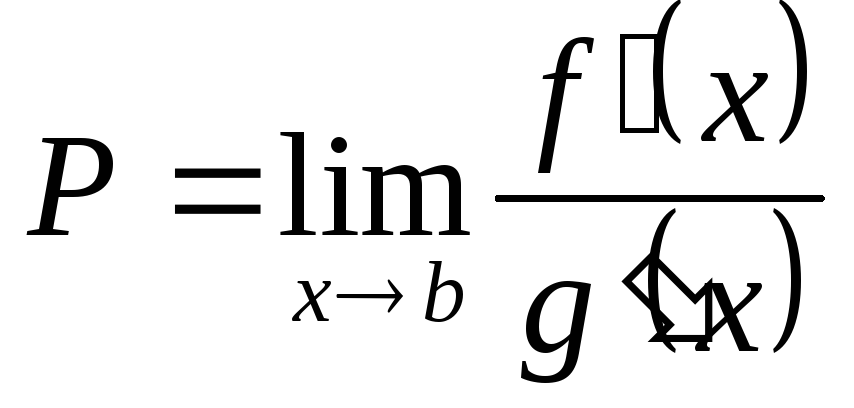 .
Доопределим функции
.
Доопределим функции
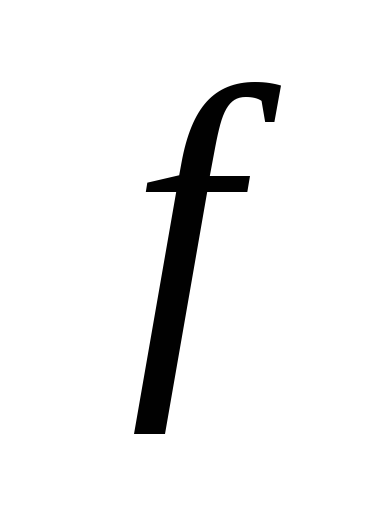 и
и
 в точке
в точке
 ,
положив
,
положив
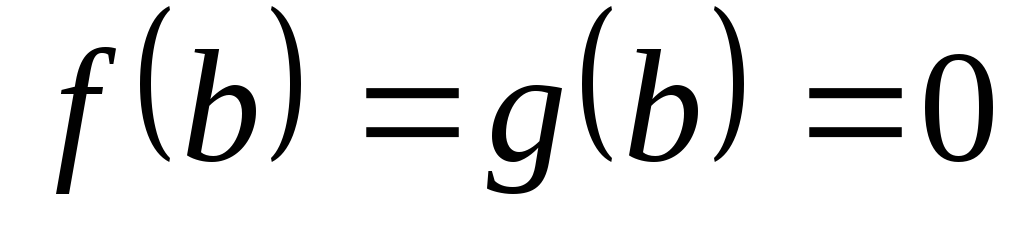 .
Тогда функции
.
Тогда функции
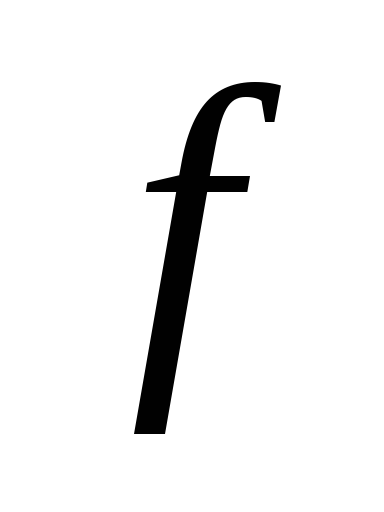 и
и
 становятся непрерывными в точке
становятся непрерывными в точке
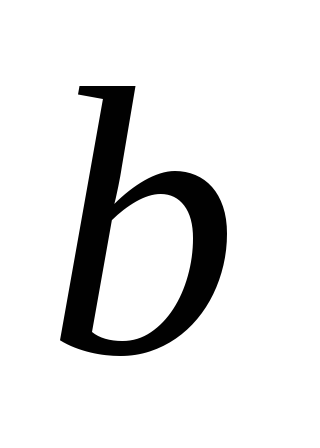 ,
и для каждого
,
и для каждого
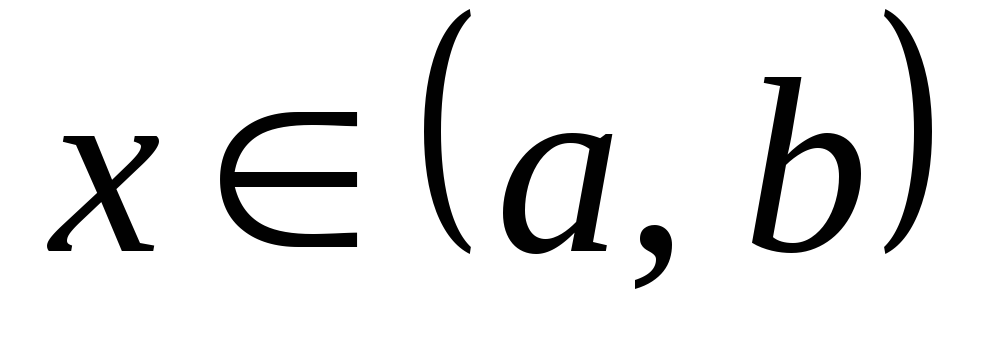 мы можем записать, используя теорему
Коши:
мы можем записать, используя теорему
Коши:
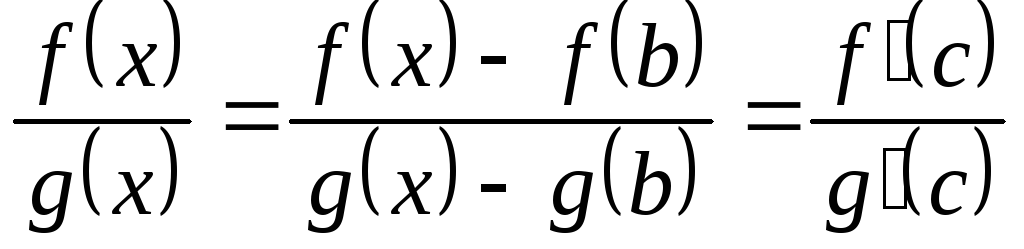 для некоторого
для некоторого
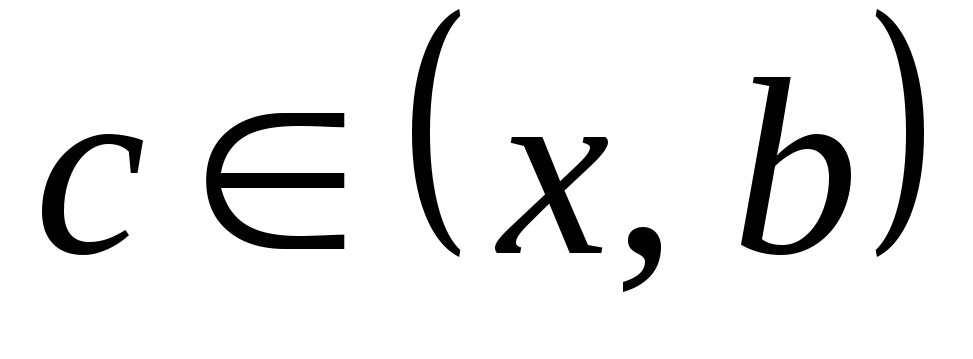 .
Ясно, что
.
Ясно, что
 зависит от
зависит от
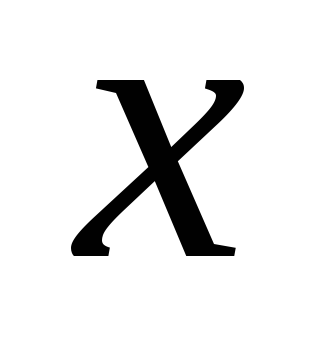 :
:
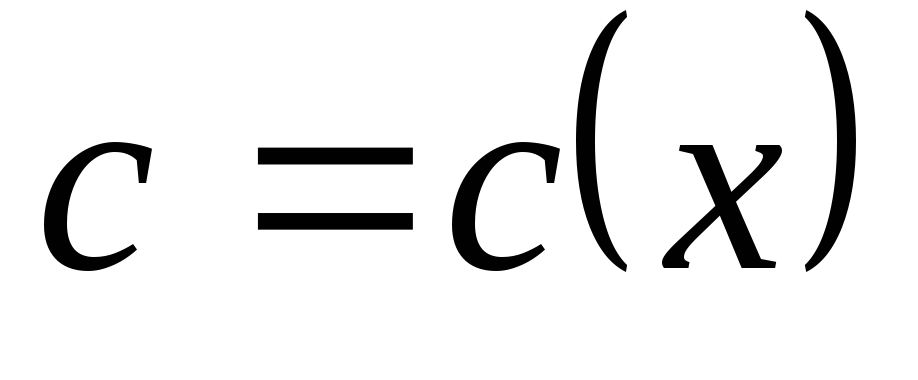 ,
причем
,
причем
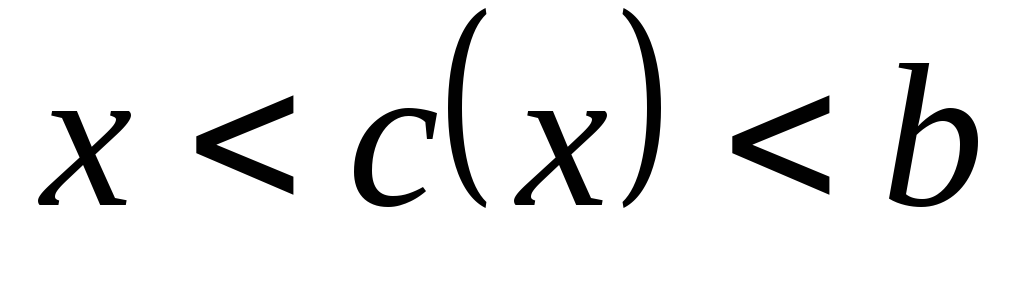 ,
откуда
,
откуда
 и
и
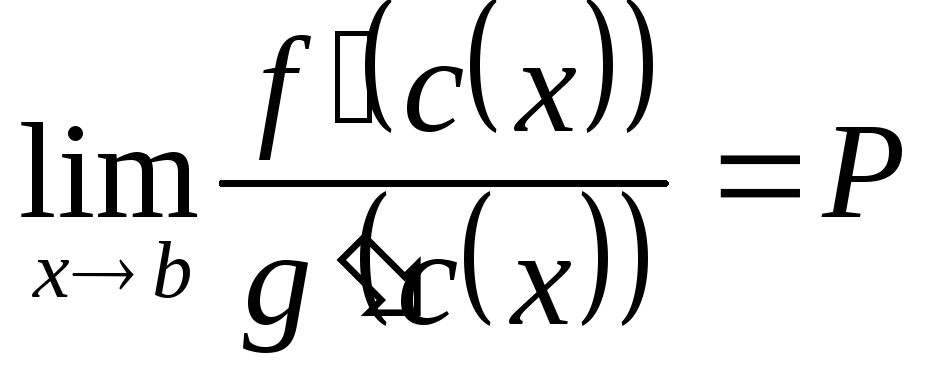 (в силу свойств предела функции).
Следовательно,
(в силу свойств предела функции).
Следовательно,
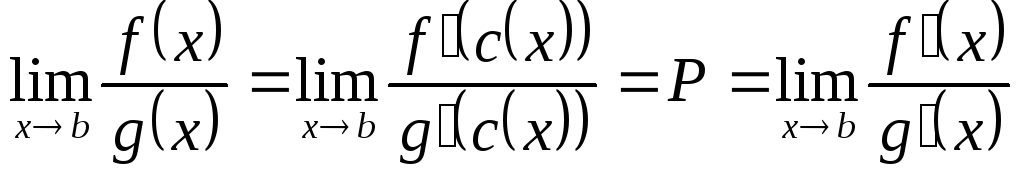 ,
теорема доказана.
,
теорема доказана.

