2. Линейная корреляция и уравнение линейной регрессии
Статистическая зависимость. При изучении взаимосвязей между разнообразными явлениями часто выясняется, что каждому значению одной переменной отвечает несколько значений другой, которые встречаются не одинаково часто.
Определение.
Если одному значению переменной
отвечает множество значений переменной
,
причем указанное множество значений
не остается постоянным, то говорят, что
между переменными
и
существует статистическая зависимость.
Этапы количественного изучения корреляционной связи:
-
Определение тесноты (силы) связи.
-
Построение теоретической линии регрессии (установление форм связи).
-
Определение значимости параметров связи.
Условным средним
называют среднее арифметическое значений
признака
,
соответствующих значению
.
Корреляционной
зависимостью
от
называют зависимость условной средней
от
:
Это уравнение регрессии
на
,
– регрессия
на
,
график
– линия регрессии
на
.
Наиболее простой формой взаимосвязи
является линейная корреляционная
зависимость. Пусть над признаками
и
проведено
наблюдений, среди которых значение
встречается
раз, значение
–
раз, пара чисел
наблюдалось
раз. Поэтому данные наблюдений удобно
представить в сгруппированном виде –
в виде корреляционной таблицы.
Уравнение прямой
линии регрессии
на
имеет вид:
,
где
– среднее признака
,
,
– среднее признака
,
,
– среднее квадратическое
отклонение признака
,
– среднее квадратическое
отклонение признака
,
Величина
называется коэффициентом
корреляции
.
Свойства коэффициента корреляции:
-
1о
Абсолютна величина коэффициента корреляции не превышает единицы
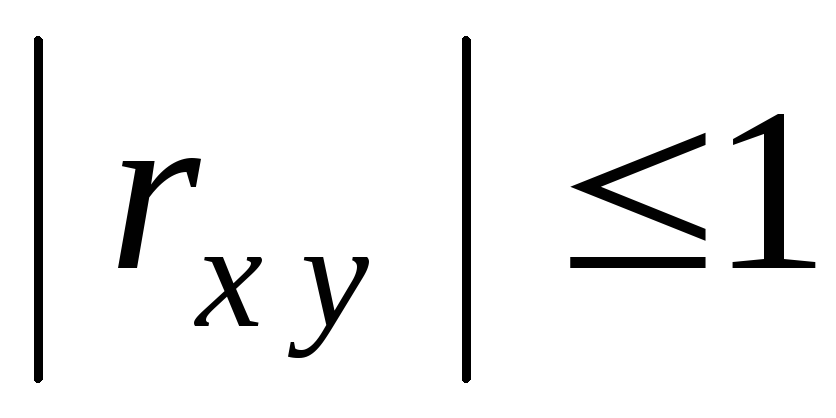.2о
Если
,
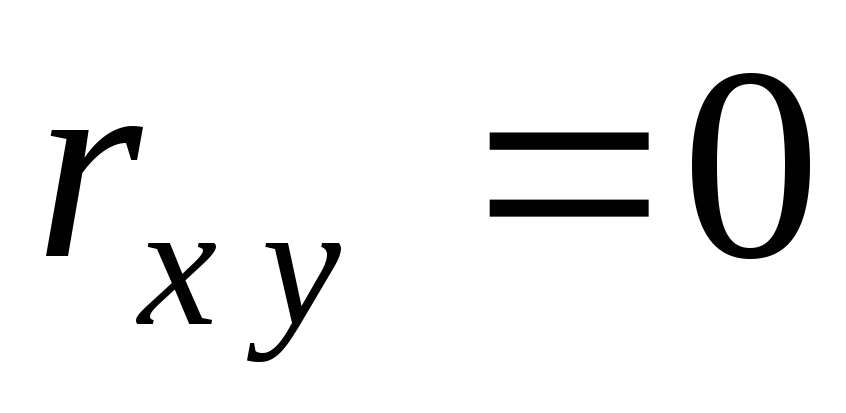то
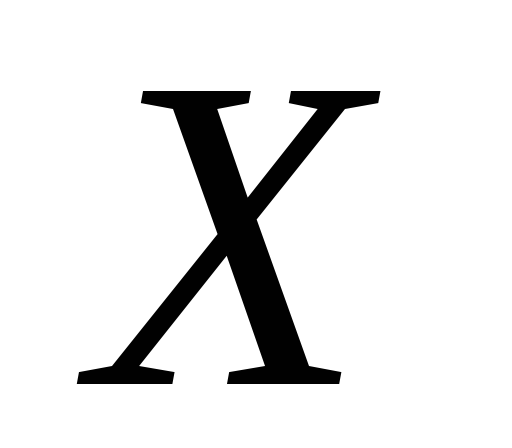и
не связаны линейной корреляционной
зависимостью.3о
С увеличением абсолютной величины коэффициента корреляции линейная корреляционная зависимость становится более тесной и при
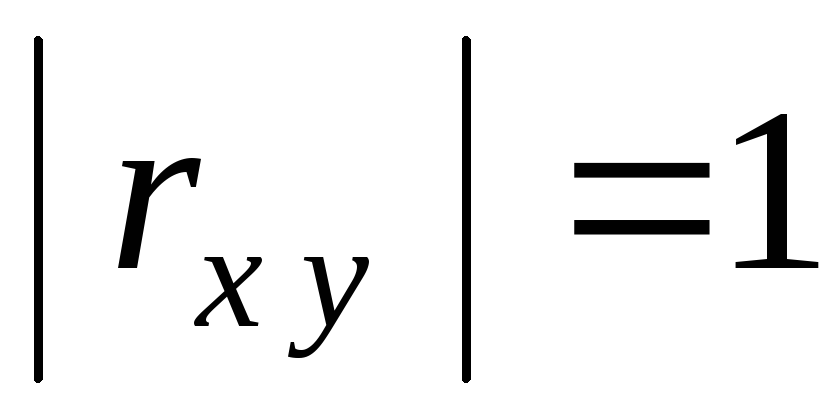превращается в функциональную
зависимость.
Коэффициент корреляции характеризует степень линейной зависимости между признаками, т.е. тесноту линейной корреляционной связи.
Если
,
то между
и
практически отсутствует линейная
корреляционная зависимость.
Если
,
то между
и
существует слабая линейная корреляционная
зависимость.
Если
,
то между
и
существует заметная линейная корреляционная
зависимость.
Если
,
то между
и
существенная линейная корреляционная
зависимость.
Если
,
то между
и
существует тесная линейная корреляционная
зависимость.
Если
,
то между
и
существует очень тесная линейная
корреляционная зависимость.
Если данные наблюдений
над признаками
и
заданы в виде
корреляционной таблицы с равноотстоящими
вариантами, то для нахождения уравнения
целесообразно использовать упрощенную
схему расчета. Идея упрощения заключается
в переходе к более простым значениям
переменных и выполнения для них основных
вычислений. Более детально указанную
идею реализуем на примере.
|
Пример 19. |
Найти
уравнение прямой линии регрессии
|
на
по сгруппированным данным корреляционной
таблицы.
-
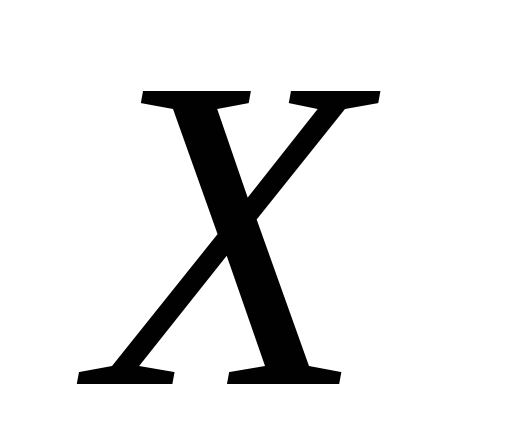
30
35
40
45
50
55
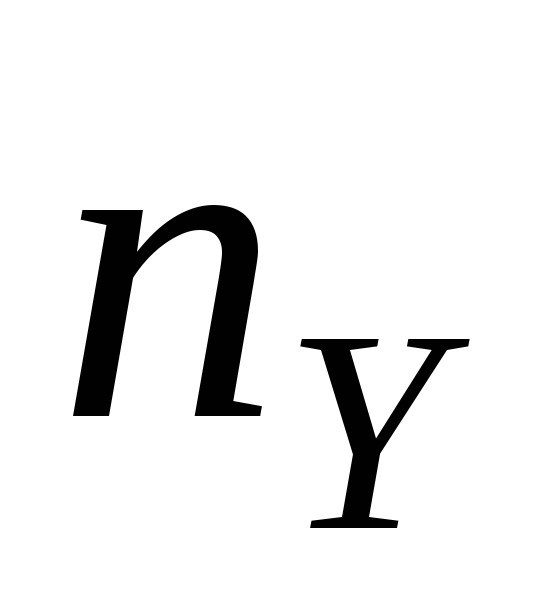
18
4
6
10
28
8
10
18
38
4
35
5
44
48
4
12
6
22
58
1
3
2
6
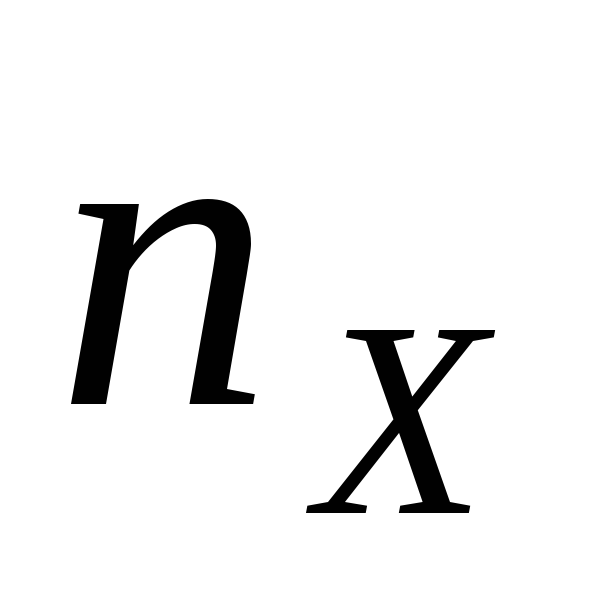
4
14
18
48
14
2
100
-
Объем выборки
.
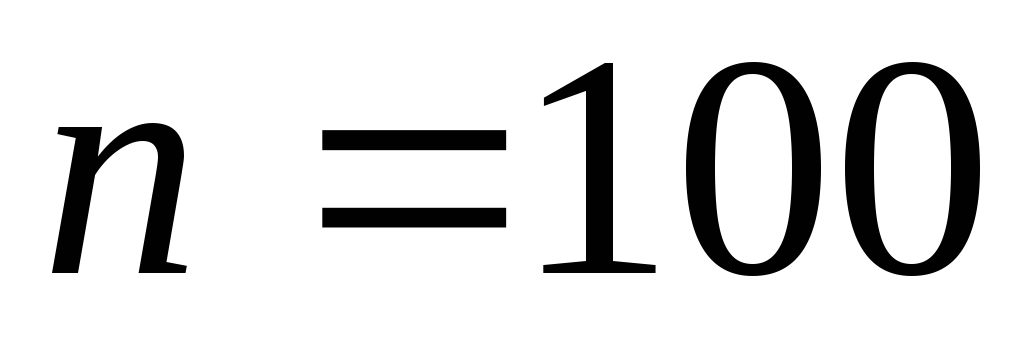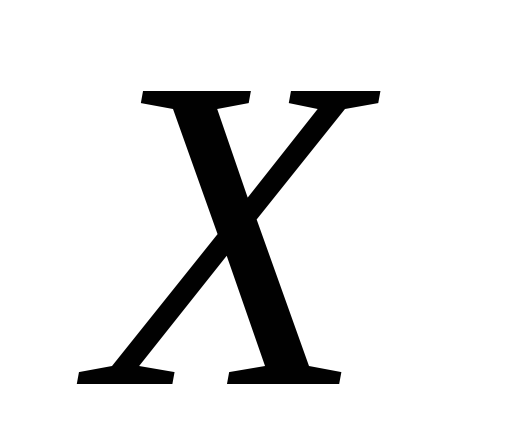Значения показателей
и
достаточно
большие, равноотстоят, можно перейти
к более простым, условным вариантам
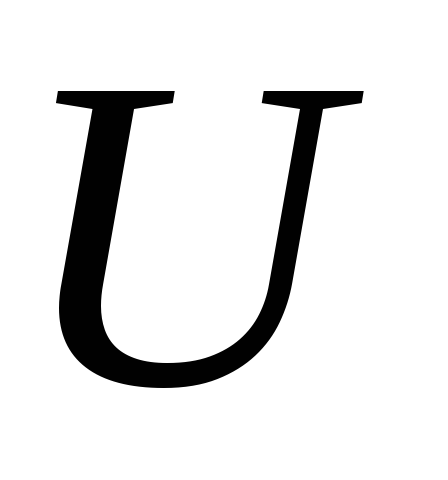и
.
а) Выбирают наибольшую
частоту в корреляционной таблице – это
35. Соответствующие этой частоте значения
показателей обозначают через
и
:
.
б) Шаг изменения
значений показателей обозначают через
и
:
(на эту величину
отличаются значения
),
(шаг для
).
в) Определяют условные варианты по формулам:
После этого составляют корреляционную таблицу в условных вариантах, сохраняя частоты.
-
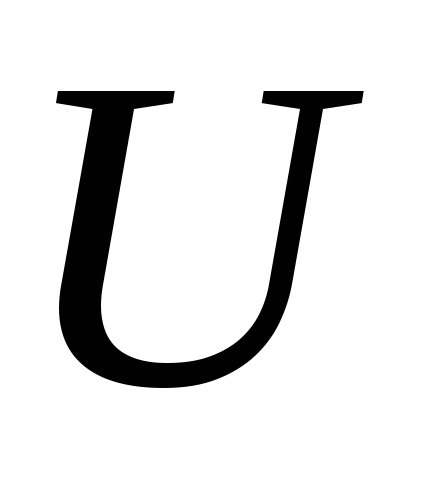
– 3
– 2
– 1
0
1
2
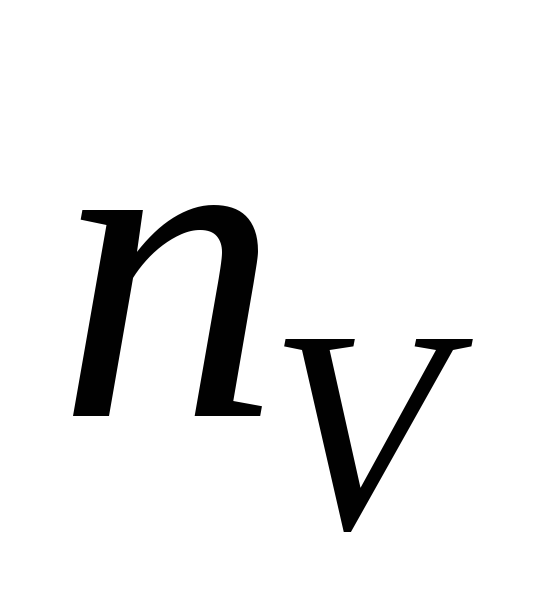
– 2
4
6
10
– 1
8
10
18
0
4
35
5
44
1
4
12
6
22
2
1
3
2
6
4
14
18
48
14
2
100
2. Проводят вычисления на основе условных вариант.
а) для
:
,
.
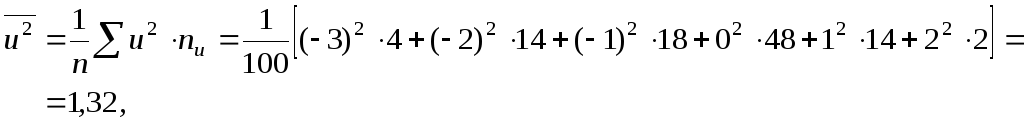
б) для
:
,
,
.
в) для
и
Найдем коэффициент корреляции:
.
Данное значение
свидетельствует о высокой степени
взаимосвязи показателей
и
,
а значит
и
.
3. Возвращаемся к старым переменным и составляем уравнение регрессии.
,
– искомое уравнение
регрессии.