12

Лабораторная работа № 4 построение схем умножения чисел, представленных в форме с фиксированной запятой, на двоичных сумматорах Цель задания

1. Изучение принципа работы схем умножения чисел, представленных в форме с фиксированной запятой.

2. Получение практических навыков построения схем умножения чисел, на двоичных сумматорах.

Постановка задачи

Для соответствующего варианта разработать и исследовать схему умножения чисел A и B, представленных в форме с фиксированной запятой на двоичных сумматорах.

Размер разрядной сетки для всех вариантов одинаковый: 2 знаковых разряда и 4 значащих цифр.

Умножение чисел осуществляется на сумматорах трех видов: двоичном сумматоре прямого кода (ДСПК), двоичном сумматоре дополнительного кода (ДСДК) и двоичном сумматоре обратного кода (ДСОК).

При разработке схемы использовать элементы серии 74.

Исходные значения чисел A и B последовательно задаются с помощью генератора слова. Эти значения должны передаваться в регистры хранения и в нужный момент извлекаться на схему умножения. Схема должна сама распознавать знак числа и в случае необходимости переводить число в другой вид. Результат умножения должен также поступать на хранение в регистр и затем отображаться любым способом.

Содержание отчета

1. Постановка задачи.

2. Основные особенности алгоритма реализации умножения чисел на двоичных сумматорах.

3. Схема для реализации умножения чисел на двоичных сумматорах.

4. .Пример умножения чисел.

5. Выводы.

Методические указания

§ 5.1. Методы умножения двоичных чисел

Применительно к двоичной системе счисления наиболее известны следующие основные способы выполнения операции умножения:

1) умножение начиная с младших разрядов множителя:

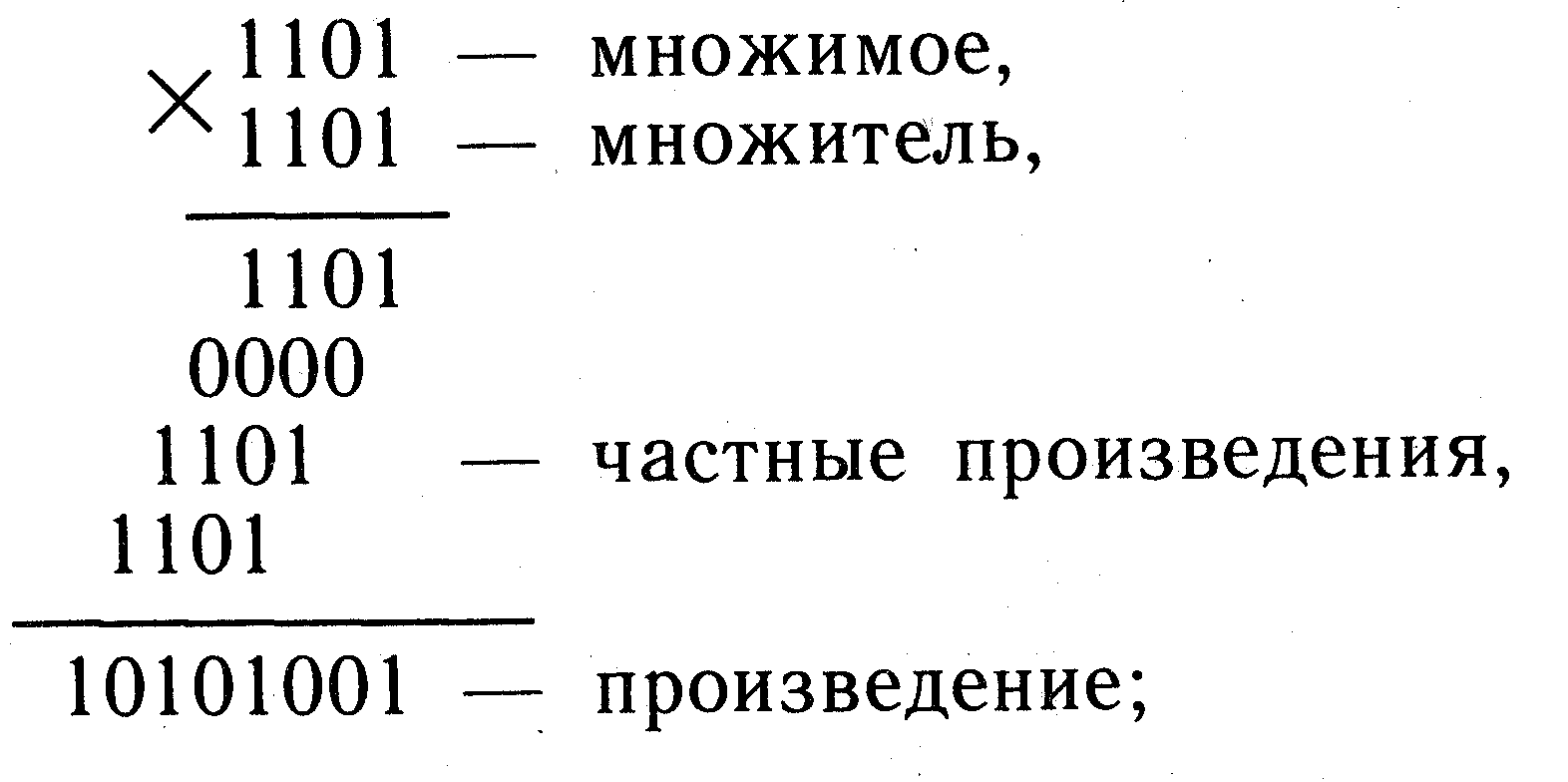
2) умножение начиная со старших разрядов множителя:

В обоих случаях операция умножения состоит из ряда последовательных операций сложения частных произведений. Операциями сложения управляют разряды множителя: если в каком-то разряде множителя находится единица, то к сумме частных произведений добавляется множимое с соответствующим сдвигом; если в разряде множителя — нуль, то множимое не прибавляется.

Таким образом, кроме операции сложения чисел для получения произведения необходима операция сдвига чисел. При этом появляется возможность сдвигать множимое или сумму частных произведений, что дает основание для разных методов реализации операции умножения.

М е т о д 1. Пусть A — множимое (A>0), множитель (B>0), С — произведение. Тогда в случае представления чисел в форме с фиксированной запятой получаем: A=0, ; B=0, Отсюда

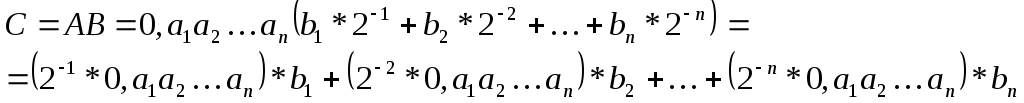(5.1)

Умножение на 2 ^-n означает сдвиг на п разрядов вправо числа, которое заключено в скобки, т. е. в данном случае сдвигается вправо множимое и умножение начинается со старших разрядов.

Структурная схема рассмотренного множительного устройства представлена на рис. 5.1, а.

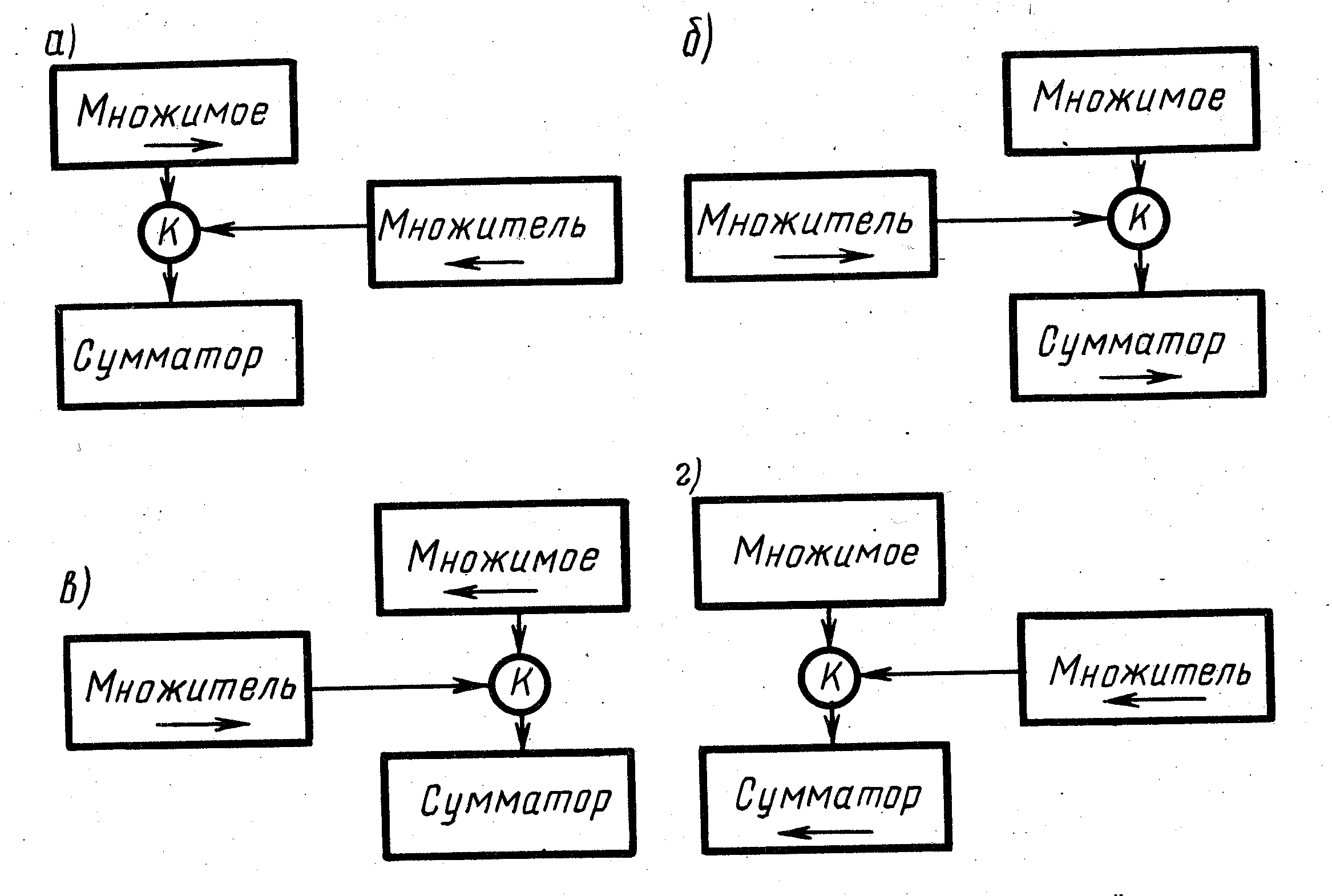
Рис. 5.1. Структурные схемы множительных устройств

Метод 2. Пусть A=0, —множимое и В=0, — множитель.

Множитель можно легко преобразовать, используя метод Горнера: . Тогда

(5.2)

Здесь умножение начинается с младших разрядов и сдвигается вправо сумма частных произведений. Структурная схема множительного устройства, реализующего этот метод, представлена на рис. 5.1, б.

Метод 3. Пусть A=0, —множимое и B=0, — множитель.

Множитель, используя метод Горнера, можно записать так:

В этом случае

(5.3)

что означает: умножение начинается с младших разрядов, и мно­жимое сдвигается влево на один разряд в каждом такте. Схема множительного устройства представлена на рис. 5.1, в.

М е т о д 4. Пусть A=0, —множимое и В=0, — множитель.

Если множитель В записать по методу Горнера

(5.4)