
- •Тема 1 рівняння математичної фізики 6
- •Тема 2 зведення рівнянь другого порядку до канонічного вигляду за допомогою заміни змінних 28
- •Тема 3 метод фур'є 55
- •Тема 4 метод сіток для рівняння параболічного типу 111
- •Тема 5 спеціальні функції математичної фізики 121
- •Передмова
- •Тема 1 рівняння математичної фізики
- •1.1 Рівняння малих поперечних коливань струни
- •1.2 Рівняння малих поздовжніх коливань стержня
- •1.3 Рівняння малих поперечних коливань мембрани
- •1.4 Телеграфне рівняння
- •1.5 Рівняння теплопровідності
- •1.6 Рівняння поширення тепла в стержні
- •1.7 Основні рівняння математичної фізики
- •Питання для самоперевірки
- •Завдання для самостійної роботи
- •Тема 2 зведення рівнянь другого порядку до канонічного вигляду за допомогою заміни змінних
- •Розв’язування
- •Розв’язування
- •2.1 Рівняння гіперболічного типу
- •Розв’язування
- •2.2 Рівняння еліптичного типу
- •Розв’язування
- •2.3 Рівняння параболічного типу
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •2.4 Розв’язування задачі Коші для рівняння коливання струни методом характеристик (формула д’Аламбера)
- •Розв’язування
- •Питання для самоперевірки
- •Завдання для самостійної роботи
- •Тема 3 метод фур'є
- •3.1 Розв’язання методом Фур’є першої крайової задачі для рівняння малих поперечних коливань струни
- •3.2 Розв’язання методом Фур’є першої крайової задачі для рівняння теплопровідності
- •3.3 Розв’язання методом Фур’є першої крайової задачі для рівняння поширення тепла у нескінченному стержні
- •3.4 Приклади розв’язання задачі Коші для рівняння теплопровідності
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •Питання для самоперевірки
- •Завдання для самостійної роботи
- •Тема 4 метод сіток для рівняння параболічного типу
- •Розв’язування
- •Питання для самоперевірки
- •Завдання для самостійної роботи
- •Тема 5 спеціальні функції математичної фізики
- •5.1 Інтеграл Ейлера першого роду
- •5.2 Інтеграл Ейлера другого роду
- •5.3 Функція Бесселя
- •5.4 Рекурентні формули для функції Бесселя
- •5.5 Інтегральне представлення Пуассона функції Бесселя та його використання
- •5.6 Сферичні функції. Поліноми Лежандра
- •5.7 Виробнича функція для поліномів Лежандра
- •5.8 Рекурентні формули для поліномів Лежандра
- •Питання для самоперевірки
- •Завдання для самостійної роботи
- •Відповіді
- •Література
- •Предметний покажчик
5.4 Рекурентні формули для функції Бесселя
Помножимо (5.11) на
![]() та продиференціюємо отриманий вираз
по
та продиференціюємо отриманий вираз
по
![]() ,
маємо
,
маємо
![]()
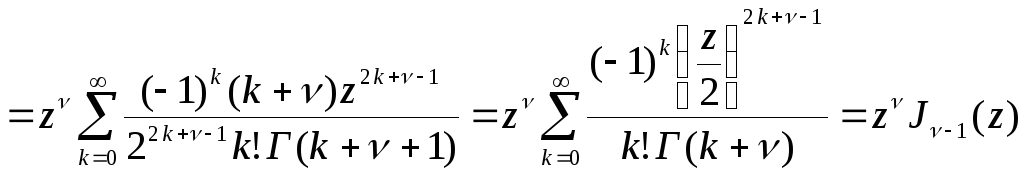 .
.
Таким чином
![]() . (5.12)
. (5.12)
Аналогічним чином можна одержати
![]() . (5.13)
. (5.13)
Продиференціювавши ліві частини рівностей (5.12) та (5.13) отримуємо
![]() , (5.14)
, (5.14)
![]() . (5.15)
. (5.15)
Звідки
![]() , (5.16)
, (5.16)
![]() . (5.17)
. (5.17)
Додавши та віднявши рівності (5.16) та (5.17), отримаємо
![]() , (5.18)
, (5.18)
![]() . (5.19)
. (5.19)
5.5 Інтегральне представлення Пуассона функції Бесселя та його використання
Циліндричні функції допускають прості інтегральні представлення. Одне з найпростіших інтегральних представлень функції Бесселя належить Пуассону.
Розглянемо
бета-функцію та її властивість
![]() .
Зробимо заміну
.
Зробимо заміну
![]() .
Тоді
.
Тоді
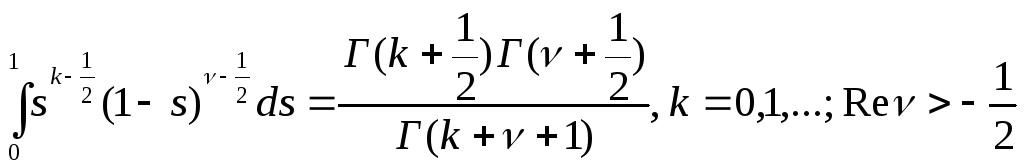 (5.20)
(5.20)
Робимо заміну
![]() ,
тоді
,
тоді
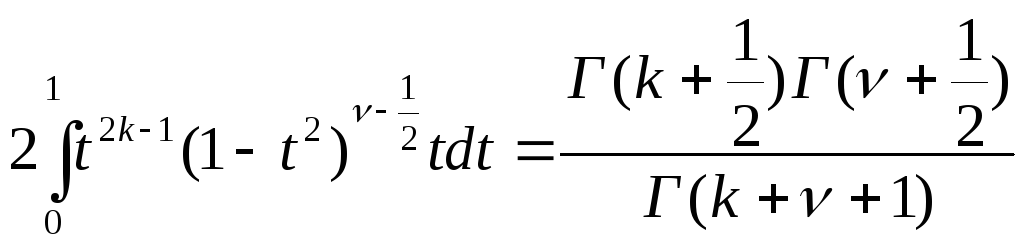 . (5.21)
. (5.21)
Звідки
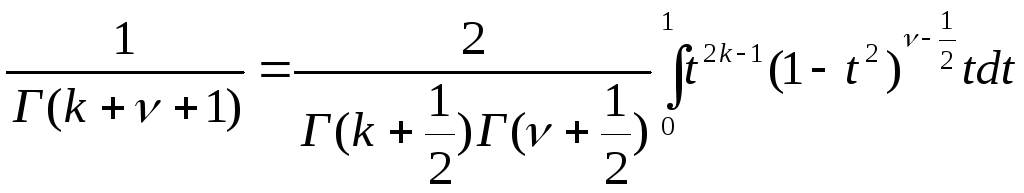 . (5.22)
. (5.22)
Підставимо рівність (5.22) у (5.11), маємо
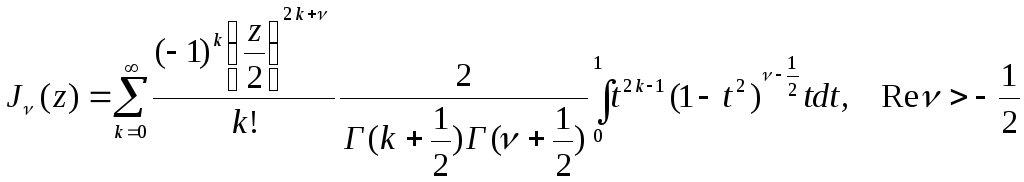 .
.
Змінимо порядок підсумовування та інтегрування, тоді
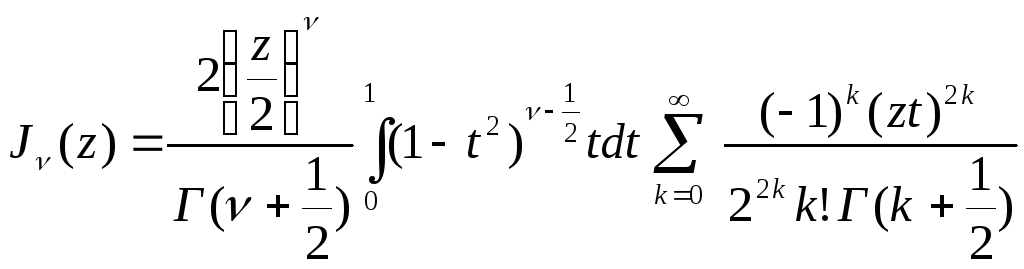 . (5.23)
. (5.23)
Скористаємося властивістю гамма-функції
![]() ,
,
в якій зробимо
заміну
![]() .
Тоді
.
Тоді
![]()
або
![]() .
.
З рівності (5.23) знаходимо
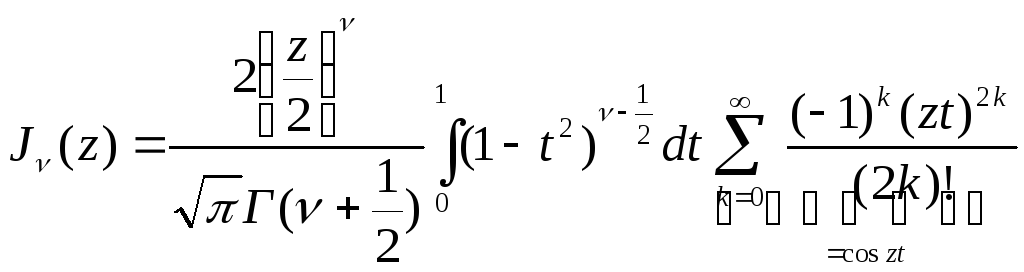 .
.
Остаточно одержуємо
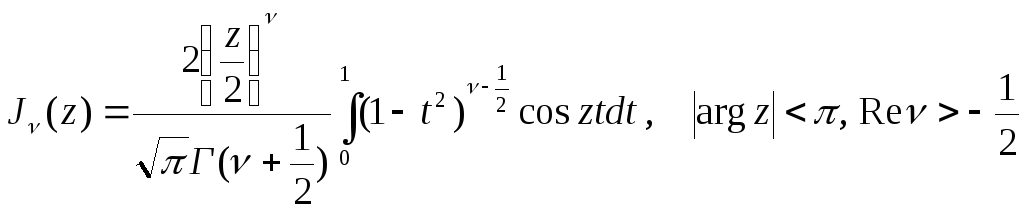 . (5.24)
. (5.24)
Оскільки підінтегральна функція парна, то формулу (5.24) можна переписати так
 (5.25)
(5.25)
Застосовуючи у
формулі (5.25) заміну
![]() ,
отримуємо
,
отримуємо
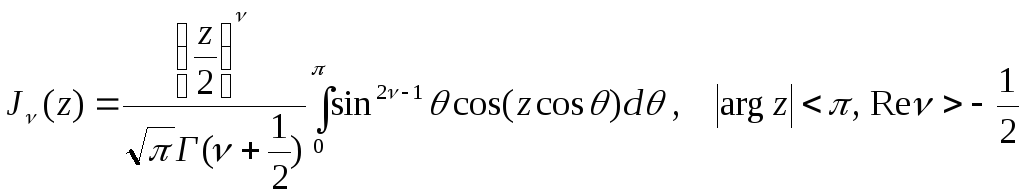 (5.26)
(5.26)
Формули (5.25) та (5.26) – інтегральне представлення Пуассона.
Приймемо у (5.24)
![]() ,
тоді
,
тоді
![]() . (5.27)
. (5.27)
Із (5.27) випливає, що
![]()
Таким чином, для
дійсних х
![]() .
.
Тепер зробимо
заміну
![]() Тоді
Тоді
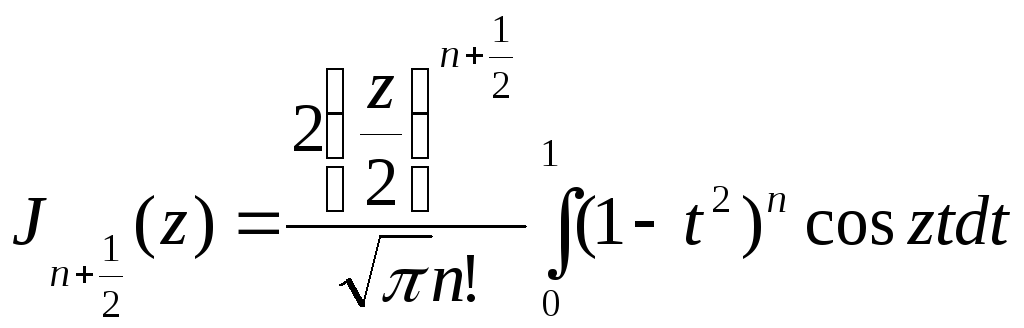 . (5.28)
. (5.28)
З рівності (5.28) випливає, що функцію Бесселя з додатним половинним індексом можна виразити за допомогою елементарних функцій. За допомогою рекурентних формул можна одержати подібний результат і для функцій з від’ємним половинним індексом. Наприклад,
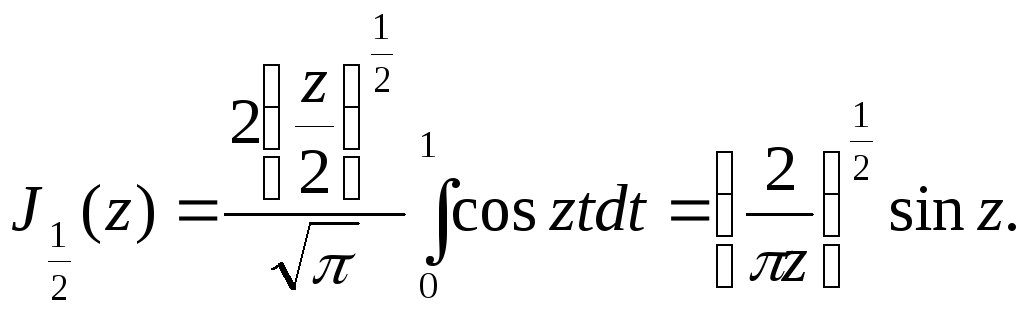
5.6 Сферичні функції. Поліноми Лежандра
Сферичними функціями називаються розв’язки лінійного диференціального рівняння
![]() , (5.29)
, (5.29)
де
![]() – комплексна змінна,
– комплексна змінна,
![]()
![]() та
та
![]() – параметри, що можуть приймати довільні
цілі додатні дійсні чи комплексні
значення.
– параметри, що можуть приймати довільні
цілі додатні дійсні чи комплексні
значення.
Рівняння (5.29) зустрічається у математичній фізиці при інтегруванні рівняння Лапласа у криволінійних координатах.
Найпростіший клас
сферичних функцій складають поліноми
Лежандра,
які є розв’язками рівняння (5.29) при
![]() .
Наступний за ступенем складності клас
сферичних функцій утворюють сферичні
функції Лежандра,
які є розв’язком рівняння (5.29) при
.
Наступний за ступенем складності клас
сферичних функцій утворюють сферичні
функції Лежандра,
які є розв’язком рівняння (5.29) при![]() і довільному дійсному чи комплексному
і довільному дійсному чи комплексному
![]() .
.
Припустимо, що у
рівнянні (5.29)
![]() ,
тобто
,
тобто
![]() . (5.30)
. (5.30)
Покажемо, що одним із інтегралів рівняння (5.30) є функція
![]() (5.31)
(5.31)
Функції (5.31) називаються поліномами Лежандра.
Позначимо
![]() .
.
Тоді
![]() ,
,
або
![]() . (5.32)
. (5.32)
Продиференціюємо рівність (5.32) (n+1) раз. Отримуємо
![]() . (5.33)
. (5.33)
Диференціювання можна виконати за формулою Лейбніца
![]() . (5.34)
. (5.34)
Позначимо для
першого доданка (5.33)
![]() ,
а для другого доданка
,
а для другого доданка
![]() .
Зрозуміло, що в обох випадках
.
Зрозуміло, що в обох випадках
![]() .
Маємо
.
Маємо
![]() ,
,
або
![]() . (5.35)
. (5.35)
Помножимо рівність
(6.35) на
![]() ,
маємо
,
маємо
![]() ,
,
або
![]() . (5.36)
. (5.36)
Рівність (5.36) означає, що поліноми Лежандра є розв’язками рівняння (5.30).
Знайдемо інший
розв’язок рівняння (5.30), який був би
лінійно незалежним з розв’язком
![]() .
.
Нехай
![]() та
та
![]() – розв’язки рівняння (5.30), тоді
– розв’язки рівняння (5.30), тоді
![]() ,
,
![]() .
.
Помножимо перше
рівняння на
![]() ,
а друге – на
,
а друге – на
![]() та віднімемо отримані рівняння, маємо
та віднімемо отримані рівняння, маємо
![]() . (5.37)
. (5.37)
Проінтегруємо тотожність (5.37)
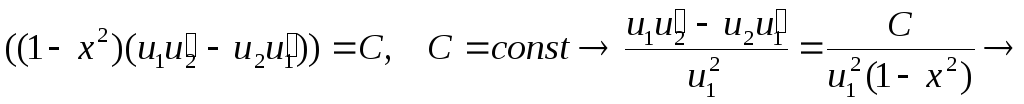
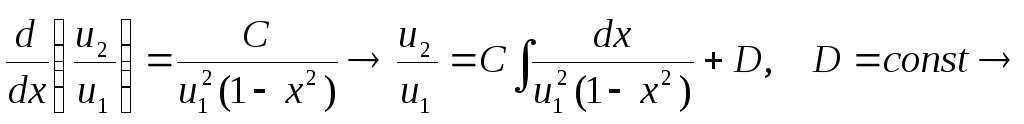
![]() . (5.38)
. (5.38)
Таким чином, якщо
![]() та
та
![]() – розв’язки рівняння (5.30), то вони
пов’язані співвідношенням (5.38), у якому
– розв’язки рівняння (5.30), то вони
пов’язані співвідношенням (5.38), у якому
![]() та
та
![]() можуть бути довільними. Якщо
можуть бути довільними. Якщо
![]() ,
то
,
то
![]() та
та
![]() лінійно незалежні. Візьмемо в якості
лінійно незалежні. Візьмемо в якості
![]() поліноми Лежандра:
поліноми Лежандра:
![]() .
Тоді, згідно з (5.38), маємо
.
Тоді, згідно з (5.38), маємо
![]() . (5.39)
. (5.39)
У рівності (5.39)
![]() – лінійно незалежна функція з
– лінійно незалежна функція з
![]() .
Функція
.
Функція
![]() називається функцією
Лежандра другого роду
(
називається функцією
Лежандра другого роду
(![]() ).
).
Нехай
![]() ,
тоді
,
тоді
![]() (5.40)
(5.40)
Візьмемо
![]() ,
тоді
,
тоді
![]() . (5.41)
. (5.41)
Нехай
![]() ,
тоді
,
тоді
![]() . (5.42)
. (5.42)
Загалом
![]() , (5.43)
, (5.43)
де
![]() – поліном степеня
– поліном степеня
![]() .
.
Оскільки функції
![]() та
та
![]() лінійно незалежні, то загальний розв’язок
рівняння (5.30) може бути записаний у
вигляді
лінійно незалежні, то загальний розв’язок
рівняння (5.30) може бути записаний у
вигляді
![]() (5.44)
(5.44)
де
![]() та
та
![]() – довільні константи.
– довільні константи.
