Розв’язування
Для розв’язання задачі використаємо стандартні засоби Maple. Задамо рівняння.
> a[1]:= 1;a[2]:=-2;a[3]:=-3;a[4]:=0;a[5]:=0;a[6]:=0;a[7]:=0;
> eq:=diff(u(x,y),x,x)-2*diff(u(x,y),x,y)-3*diff(u(x,y),y,y)=0;
eq:=
Використаємо стандартну програму Maple - mapde(eq,canom). Ця програма перетворює початкове рівняння в простіше. Фактично, це ще один спосіб зведення заданого рівняння до канонічного вигляду.
> with(PDEtools):
> mapde(eq,canom);
&where
> op(%);
,
Знайдемо тепер загальний розв’язок одержаного рівняння гіперболічного типу
> pdsolve(%[1]);
Повернемось до старих змінних
> sol:=u(x,y)=subs(%%[2],rhs(%));
Перевіримо знайдений розв’язок.
> simplify(subs(sol,eq));
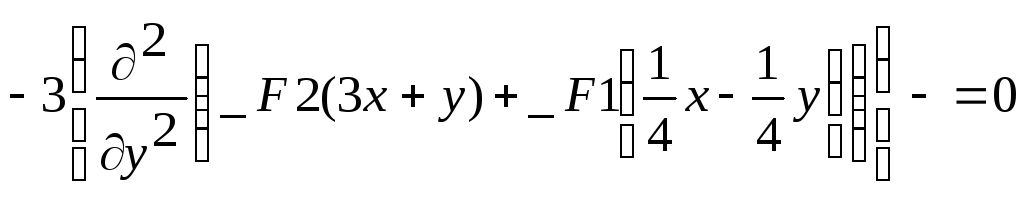
> simplify(lhs(%));
Приклад 2.9 Знайти загальний розв’язок рівняння зі сталими коефіцієнтами.
Розв’язування
Для розв’язання задачі використаємо стандартні засоби Maple. Задамо рівняння.
> a[1]:= 1;a[2]:=-4;a[3]:=-5;a[4]:=0;a[5]:=0;a[6]:=0;a[7]:=0;
> eq:=diff(u(x,y),x,x)-2*diff(u(x,y),x,y)-3*diff(u(x,y),y,y)=0;
eq:=
Використаємо стандартну програму Maple - mapde(eq,canom). Ця програма перетворює початкове рівняння в простіше. Фактично, це ще один спосіб зведення заданого рівняння до канонічного вигляду.
> with(PDEtools):
> mapde(eq,canom);
&where
> op(%);
,
Знайдемо тепер загальний розв’язок одержаного рівняння гіперболічного типу
> pdsolve(%[1]);
Повернемось до старих змінних
> sol:=u(x,y)=subs(%%[2],rhs(%));
Перевіримо знайдений розв’язок.
> simplify(subs(sol,eq));
> simplify(lhs(%));
2.4 Розв’язування задачі Коші для рівняння коливання струни методом характеристик (формула д’Аламбера)
Розрізняють три типи крайових задач для диференціальних рівнянь:
-
Задача Коші для рівнянь гіперболічного та параболічного, типу у якій задаються тільки початкові умови;
-
Крайова задача для рівнянь еліптичного типу у якій відсутні початкові умови;
-
Змішана задача для рівнянь гіперболічного та параболічного типу, у якій ставляться як крайові, так і початкові умови.
Відмітимо, що методом характеристик називається метод розв’язування лінійних диференціальних рівнянь у частинних похідних другого порядку шляхом інтегрування їх канонічних форм.
Коливання
струни описується рівнянням
з початковими умовами
,
,
де
–
початкове
відхилення струни від положення
рівноваги,
–
початкова
швидкість точок струни.
Тоді рівняння характеристик такі:
та
. (2.26)
Розв’язками рівнянь (2.26) будуть
та
. (2.27)
Згідно з (2.27) потрібно ввести заміну
та
. (2.28)
Враховуючи формули (2.4), рівняння коливання струни буде таке:
, (2.29)
або
. (2.30)
З рівняння (2.30) випливає, що
. (2.31)
Для
знаходження функції
проінтегруємо рівняння (2.31) за змінною
,
маємо
. (3.7)
Введемо позначення
. (2.32)
Враховуючи (2.33), (2.28) рівність (2.32) виглядатиме так
. (2.34)
Для
того, щоб знайти функції
та
,
скористаємося
початковими умовами. Тоді
, (2.35)
.
(2.36)
Рівність (2.36) можна переписати так
. (2.37)
Проінтегруємо (2.37) в межах від 0 до х, маємо
, (2.38)
звідки
. (2.39)
Позначимо
,
тоді
з рівності (2.39) маємо:
. (2.40)
Таким
чином, враховуючи (2.35) та (2.40), ми отримали
систему для знаходження функцій
та
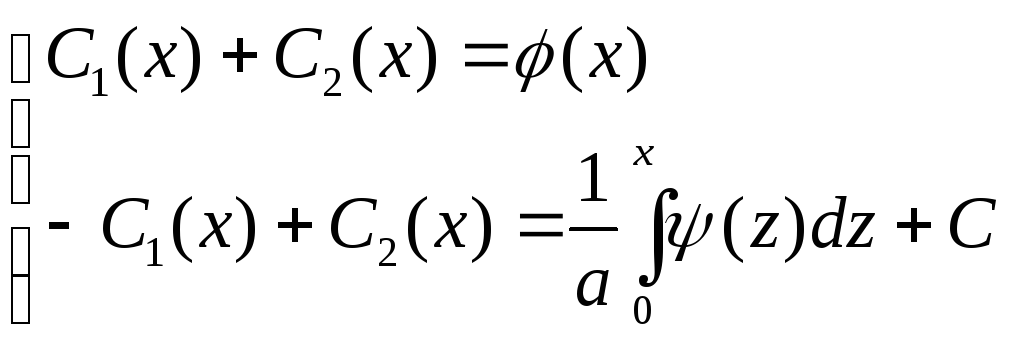. (2.41)
Системою розв’язків системи (2.41) буде
. (2.42)
Згідно з заміною (2.28) одержуємо
,
(2.43)
.
Підставивши
рівності (2.43) у (2.34) знайдемо функцію
. (2.44)
Формула (2.44) називається формулою Д’Аламбера.
У випадку, коли коливання струни описується рівнянням вигляду
(2.45)
з початковими умовами
,
, (2.46)
де
–
початкове
відхилення струни від положення
рівноваги,
–
початкова
швидкість точок струни, формула Д’Аламбера
записується так
.
(2.47)
Приклад
2.10 Знайти
розв’язок задачі Коші за формулою
Д’Аламбера
за умови, що
,
.
Розв’язування
Згідно з формулою (2.44) знайдемо спочатку інтеграл
.
Тоді
.
Приклад
2.11 Знайти
розв’язок задачі Коші за формулою
Д’Аламбера
за умови, що
,
.
Розв’язування
В даному випадку потрібно скористатись формулою (2.47).
Для цього обчислимо інтеграли
.
Оскільки
,
то
.
Приклад
2.12 Коливання
струни описується рівнянням
з початковими умовами
,
,
де
.
Знайти розв’язок задачі Коші за формулою
Д’Аламбера.
Розв’язування
За
формулою Д’Аламбера
.
Знайдемо
спочатку інтеграл
> Int(cos(z),z=x-at..x+at)=int(cos(x),x=x-at..x+at);
Тоді
Приклад
2.13
Коливання струни описується рівнянням
з початковими умовами
,
,
де
.
Знайти розв’язок задачі Коші за формулою
Д’Аламбера.
Розв’язування
В даному випадку потрібно використати формулу
Для цього обчислимо інтеграли, які є складовими даної формули.
Розв’язуємо задачу в системі аналітичних обчислень Maple.
> a:=1;f(xi,eta):=6;
> with(student):
> 1/2*a*Doubleint(f(xi,eta),xi=x-t+eta..x+t-eta,eta=0..t);
> z:=value(%);
> psi(xi):=4*x;a:=1;
>d:=1/2*a*Int(psi(xi),xi=x-a*t..x+a*t)=1/2*a*int(psi(xi),xi=x-a*t..x +a*t);
Оскільки
,
то
Приклад
2.14
Коливання струни описується рівнянням
з початковими умовами
,
,
де
,
,
,
.
Знайти розв’язок задачі Коші за формулою
Д’Аламбера.