- •Асимптоты.
- •Из таблицы следует, что меняет знак при переходе через точку , но тогда по теореме 6 эта точка является абсциссой точки перегиба.
- •Знаки функций. , если и , если . Корни уравнения известны: и . Кривая знаков имеет вид (рис.12) рис.13
- •Строим график функции (рис.15)
- •Литература.
- •Предельная себестоимость характеризует себестоимость c прироста продукции q
- •II. Исследование функций с помощью производных.
-
Данная функция - четная, ее график симметричен относительно оси
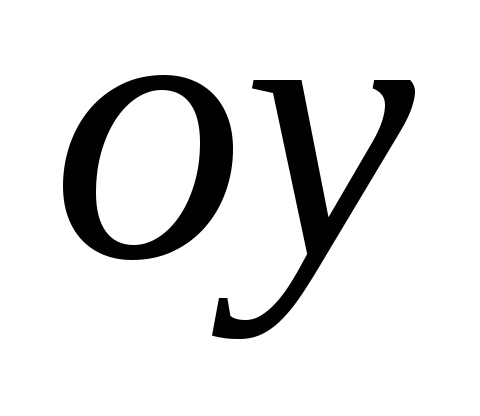 .
Поэтому исследуем функцию для
.
Поэтому исследуем функцию для
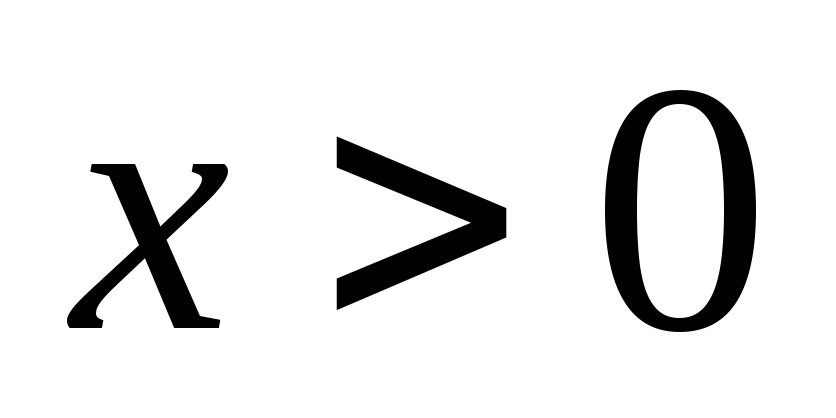 ,
а при построении графика воспользуемся
симметрией и продлим его для
,
а при построении графика воспользуемся
симметрией и продлим его для
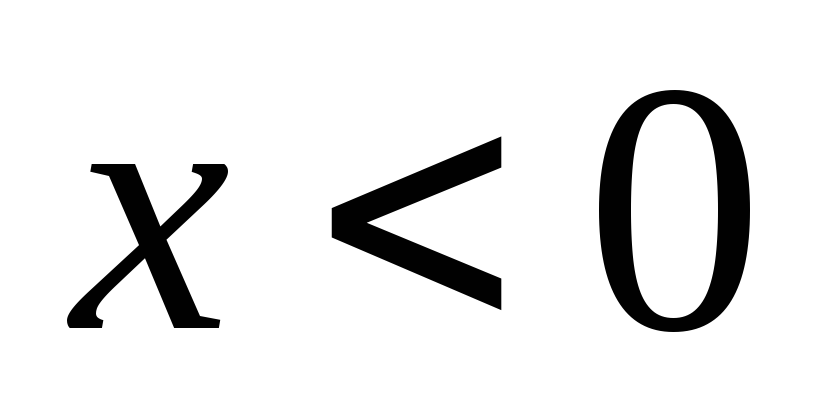 .
. -
При
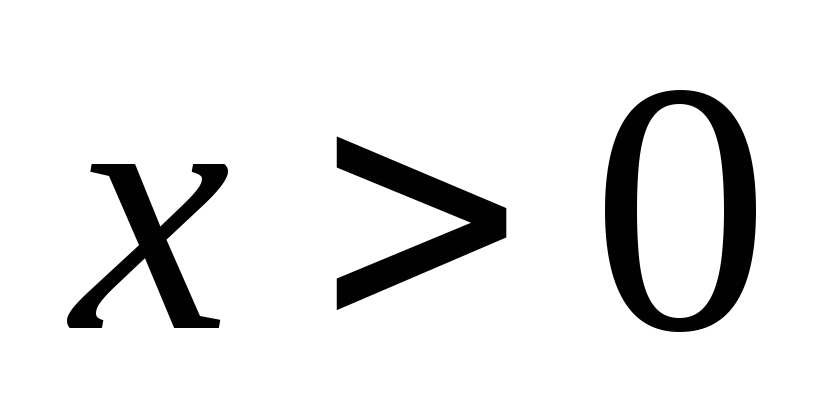 рассмотрим функцию
рассмотрим функцию
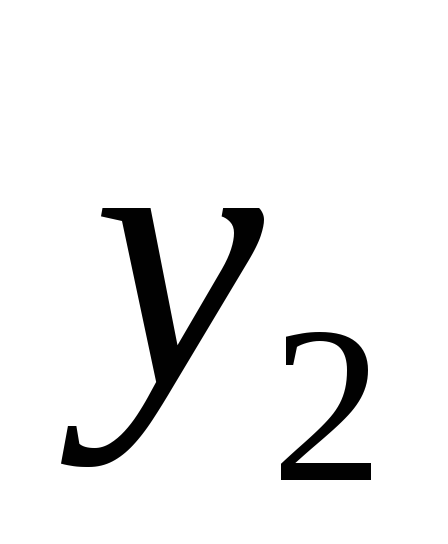 и
и
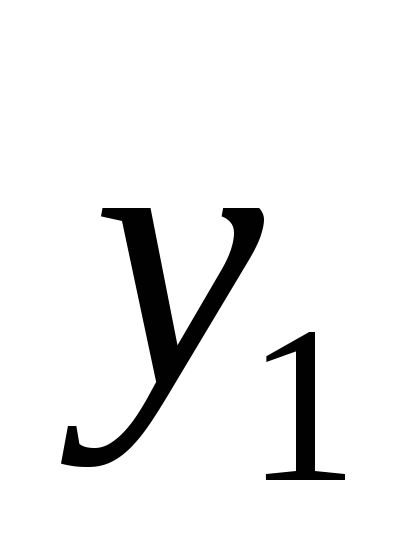 :
:
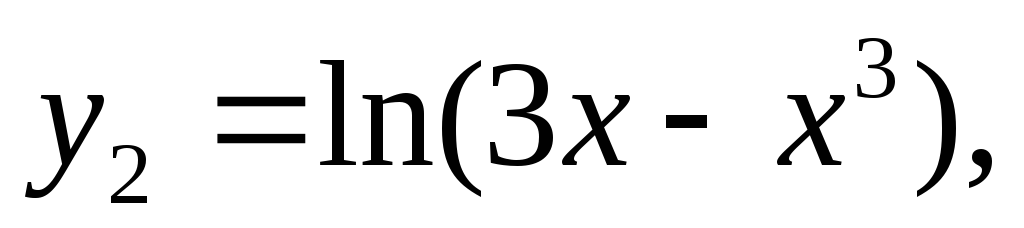 где
где
 и
и
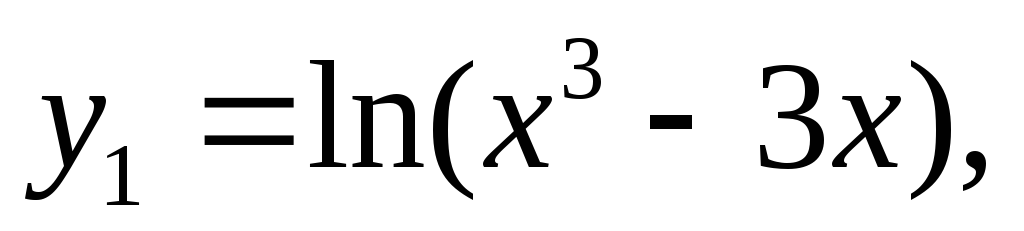 где
где
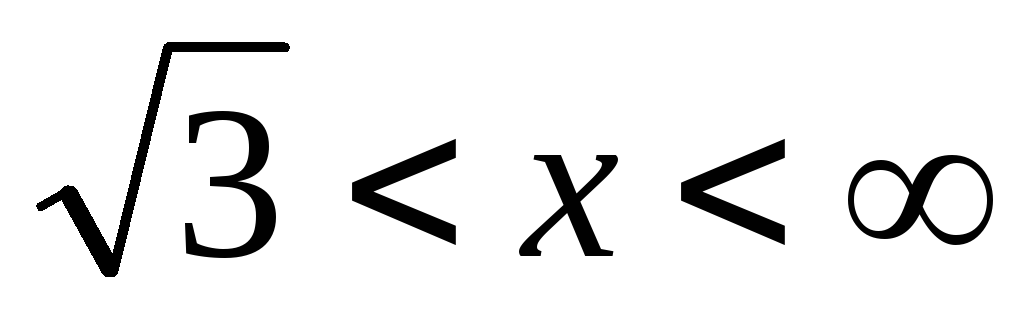 .
Обе
эти функции общего вида с осью
.
Обе
эти функции общего вида с осью
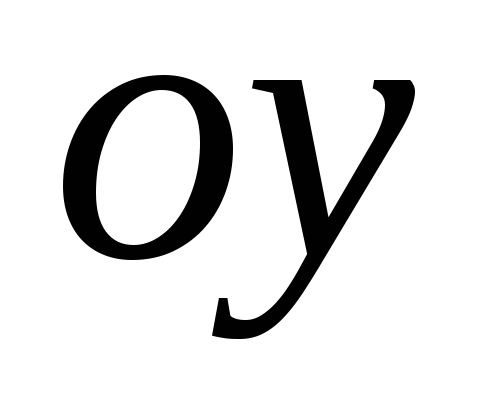 не пересекаются, а с осью
не пересекаются, а с осью
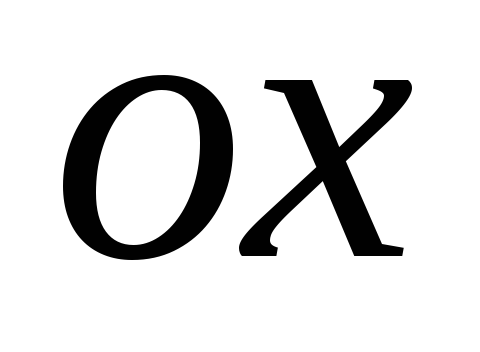
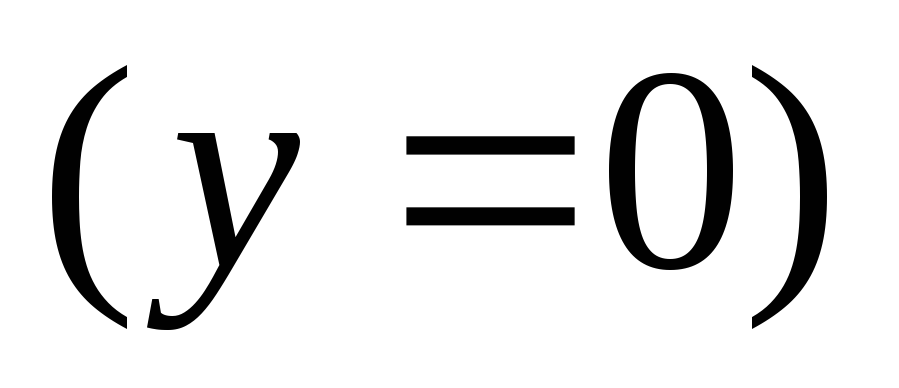 пересекаются в точках, определяемых
уравнениями, полученными на основании
свойства: логарифм единицы равен
нулю.
Таким образом, график функции
пересекаются в точках, определяемых
уравнениями, полученными на основании
свойства: логарифм единицы равен
нулю.
Таким образом, график функции
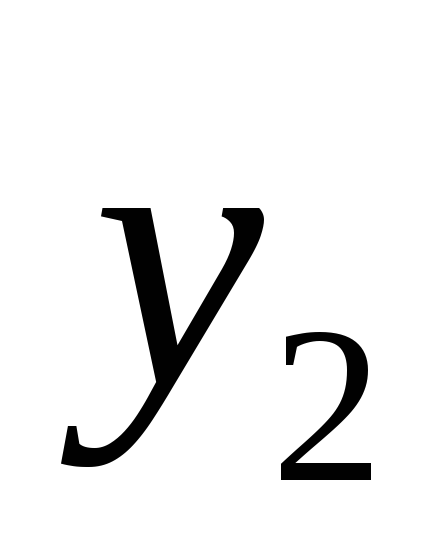 пересекается с осью
пересекается с осью
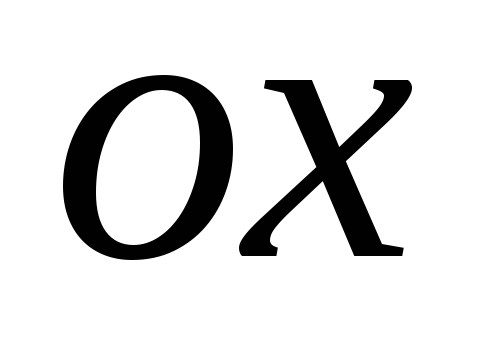 в точках, удовлетворяющих уравнению:
в точках, удовлетворяющих уравнению:
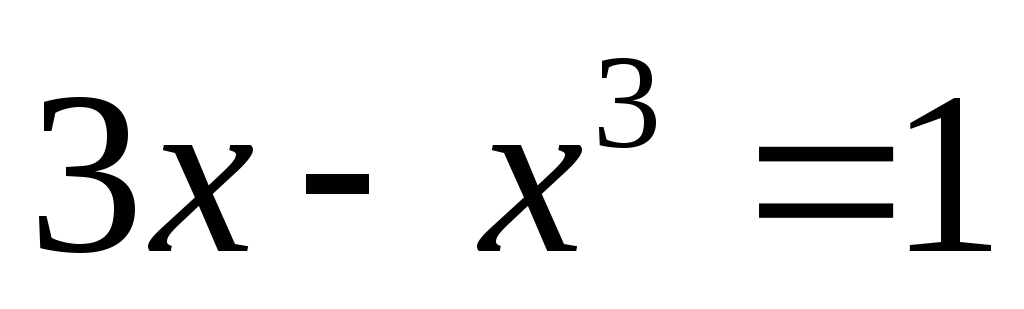 ,
а
график функции
,
а
график функции
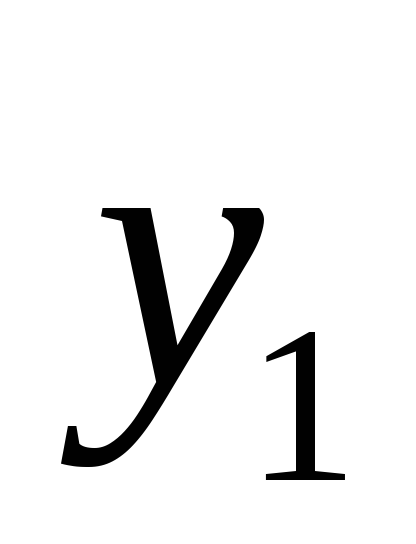 - в точках, удовлетворяющих
уравнению:
- в точках, удовлетворяющих
уравнению:
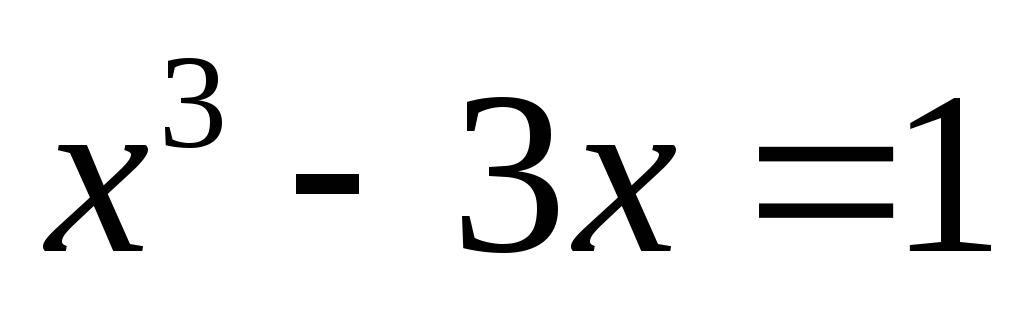 .
Решая
эти уравнения графически, получим для
каждого из них три действительных
корня. Для уравнения
.
Решая
эти уравнения графически, получим для
каждого из них три действительных
корня. Для уравнения
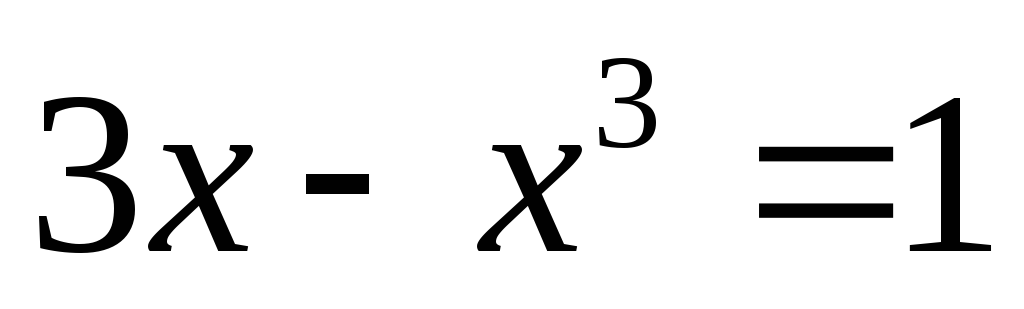 получим:
получим:
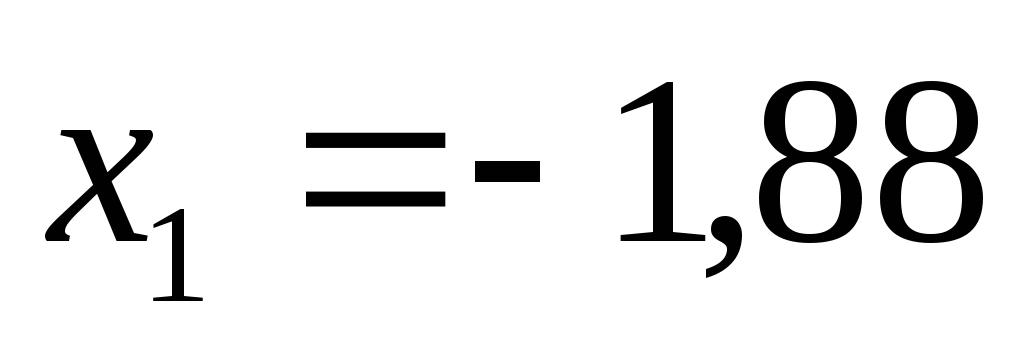 ,
,
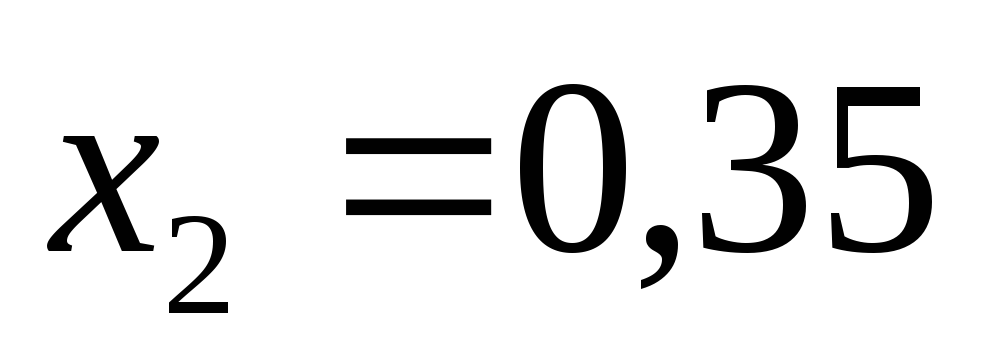 и
и
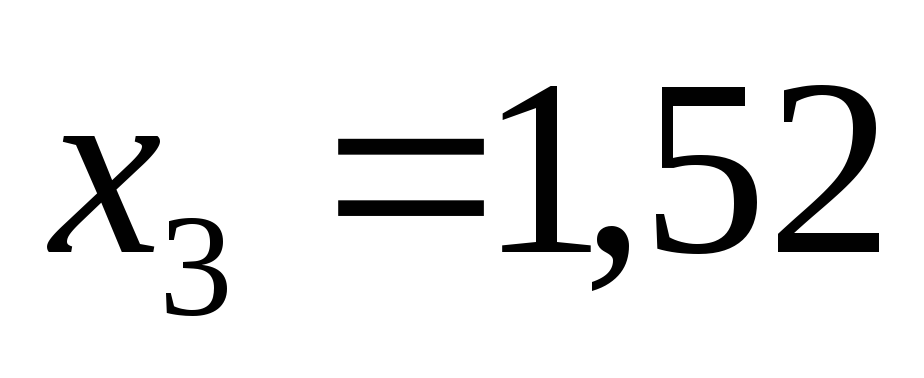 ,
а для уравнения
,
а для уравнения
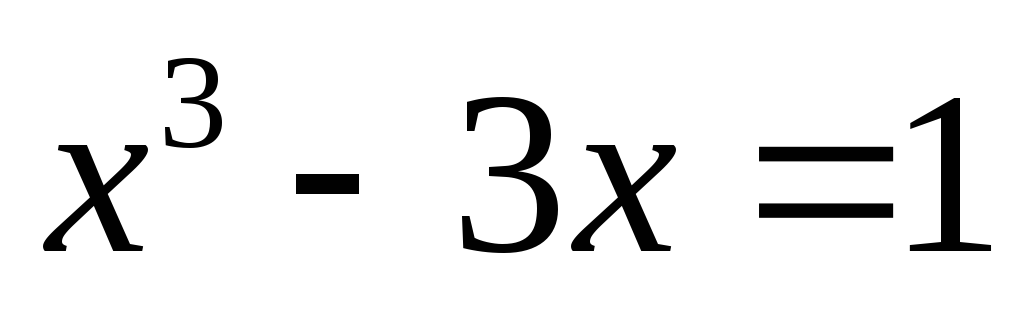 получим:
получим:
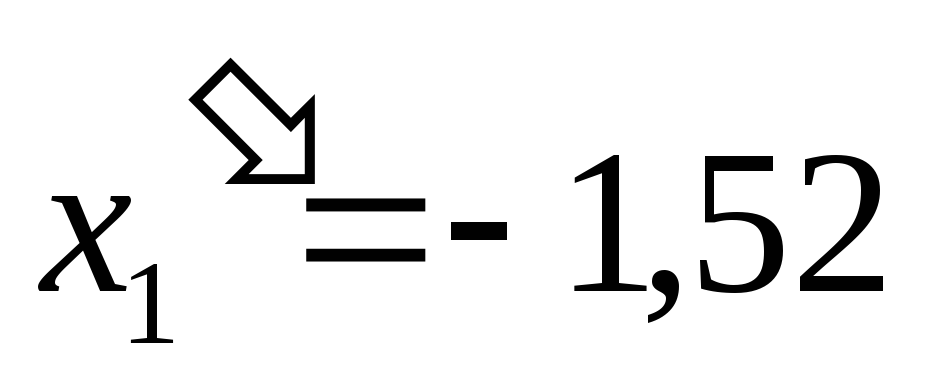 ,
,
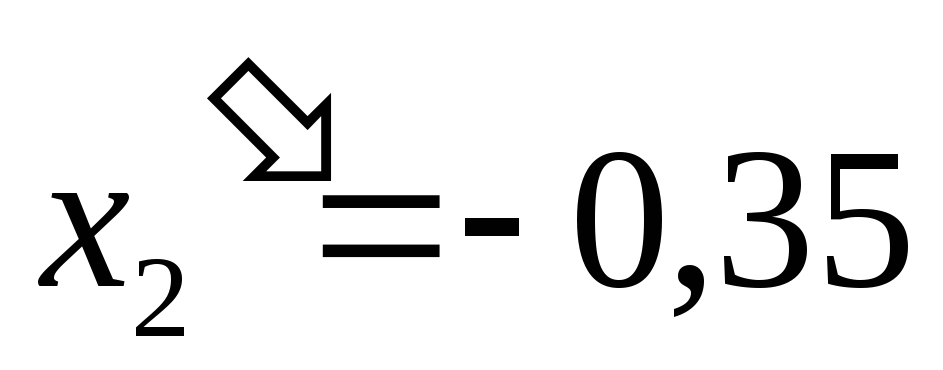 ,
,
 .
Принимая во внимание ОДЗ каждой функции
и то, что
.
Принимая во внимание ОДЗ каждой функции
и то, что
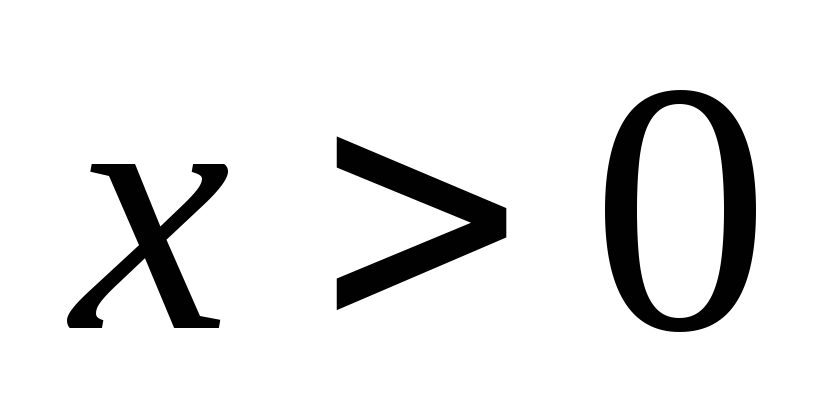 ,
приходим к выводу, что функция
,
приходим к выводу, что функция
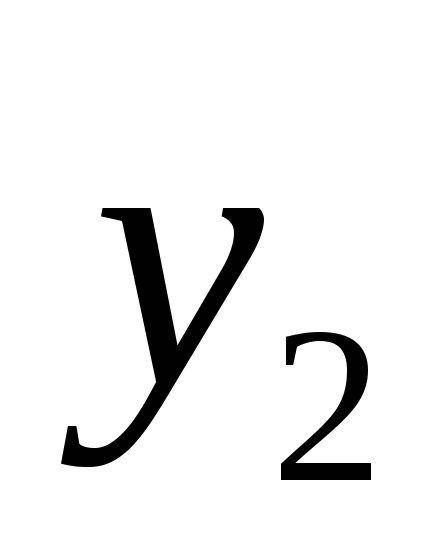 пересекает ось
пересекает ось
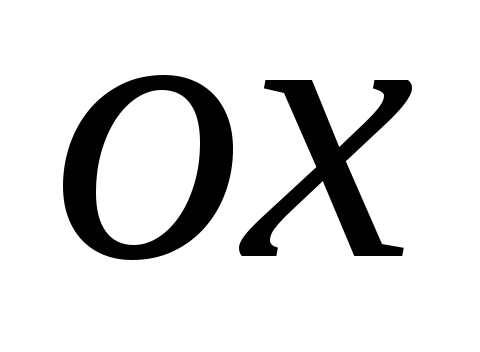 в точках
в точках
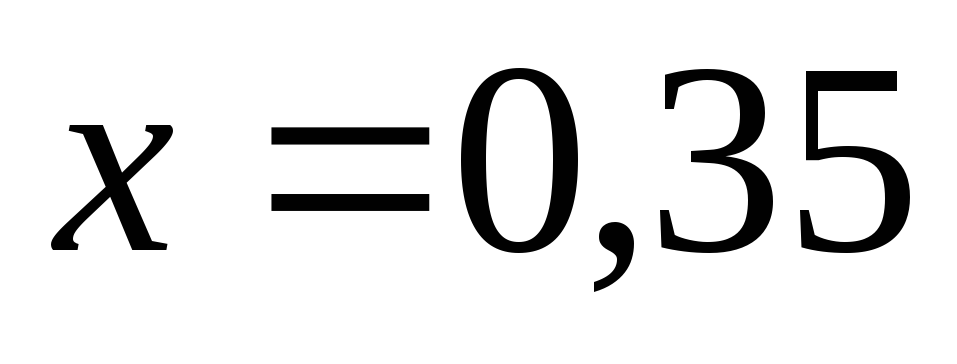 и
и
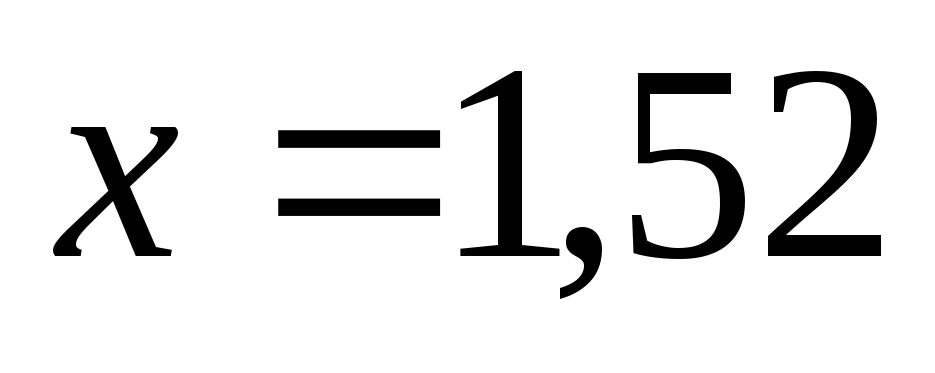 ,
а функция
,
а функция
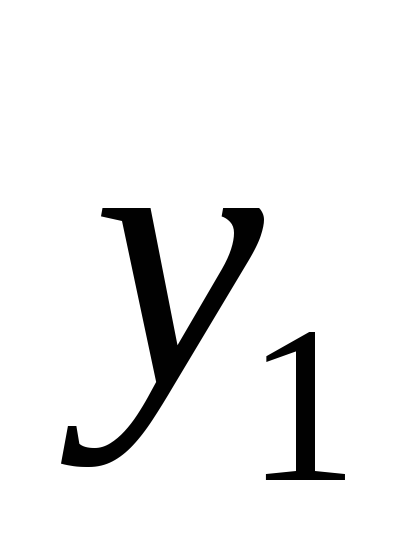 - в точке
- в точке
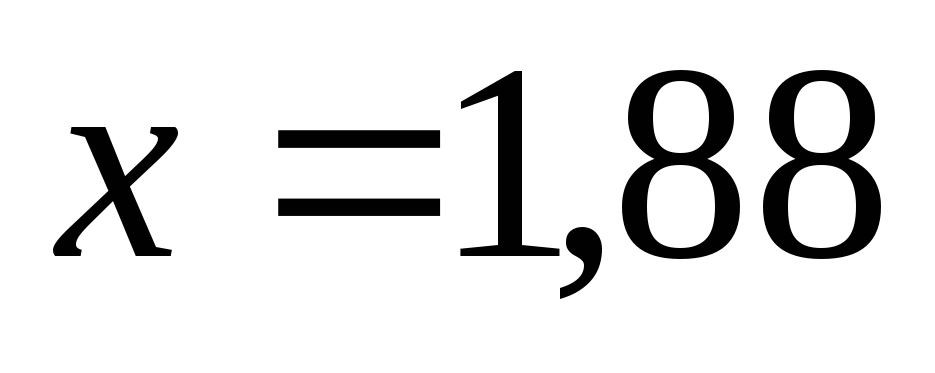 .
. -
Знаки функций. , если и , если . Корни уравнения известны: и . Кривая знаков имеет вид (рис.12) рис.13
Откуда
заключаем:
![]() ,
если
,
если
![]() и
и
![]() ,
если
,
если
![]() и
и
![]() .
.
Для
функции
![]() находим, что
находим, что
![]() ,
если
,
если
![]() .
.
-
Вычисляем производные:
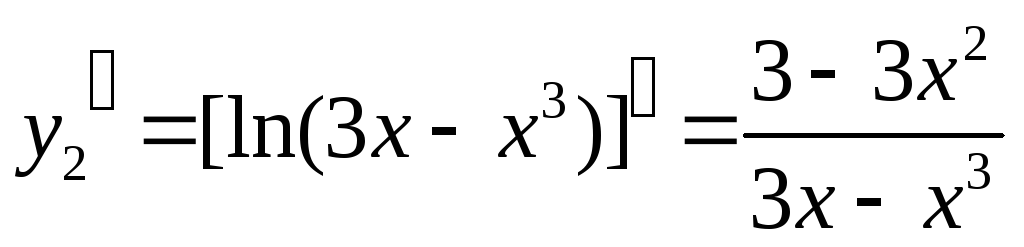
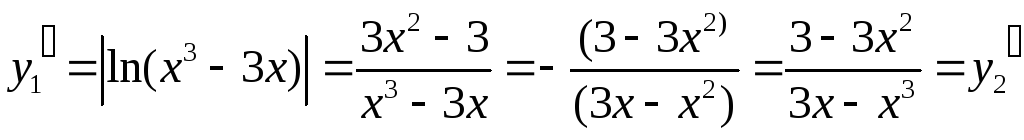 Получаем:
Получаем:
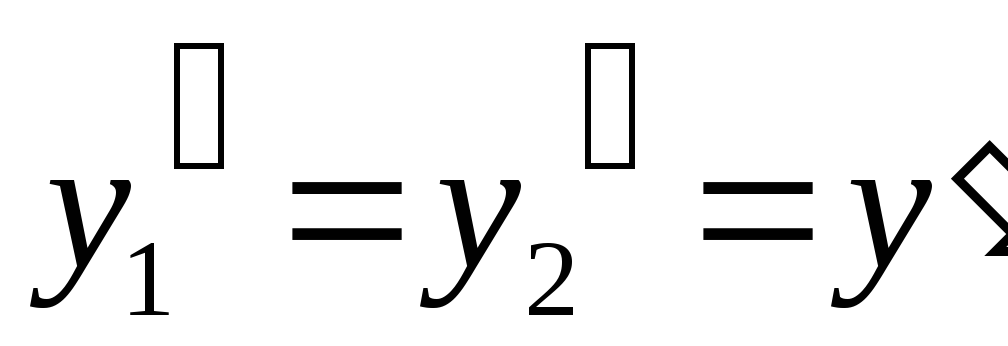 .
Производная
.
Производная
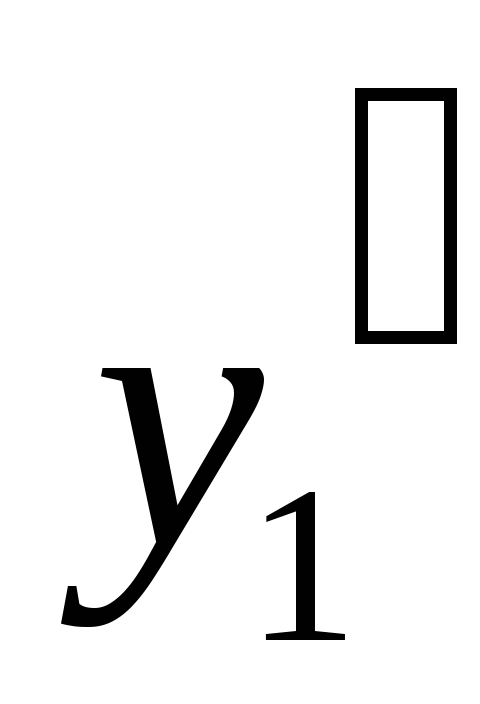 и
и
 равна нулю в точках
равна нулю в точках
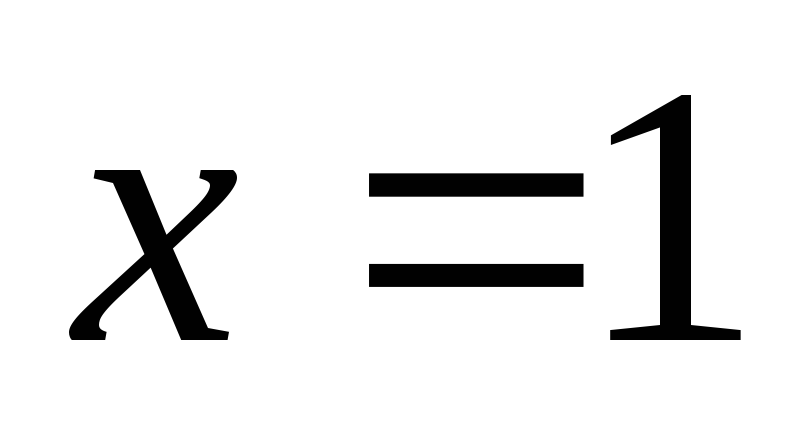 и
и
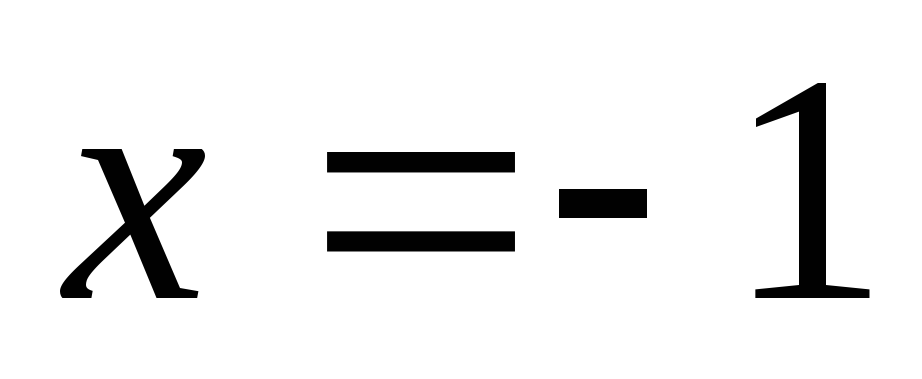 и не существуют в точках:
и не существуют в точках:
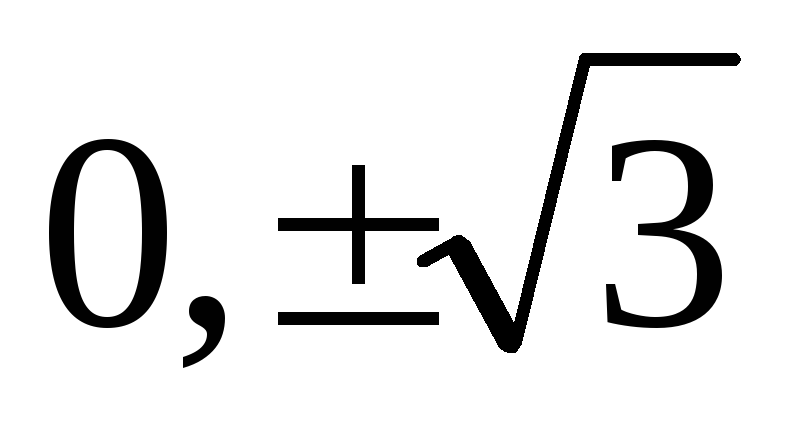 ,
которые не входят в ОДЗ, таким образом
подозрительной на экстремум точкой
является только
,
которые не входят в ОДЗ, таким образом
подозрительной на экстремум точкой
является только
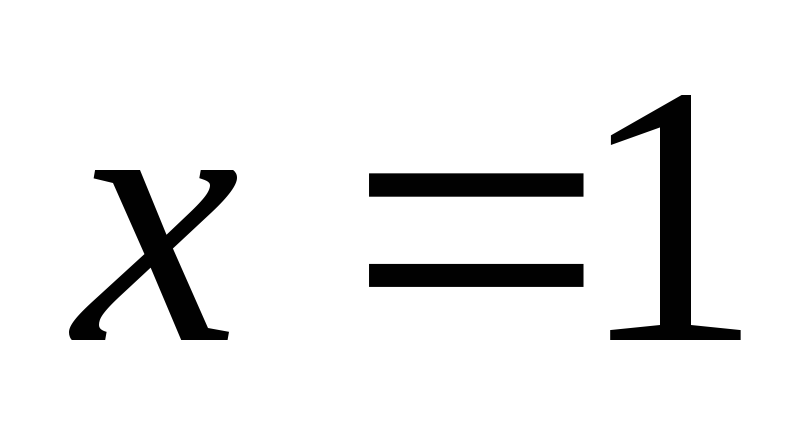 .
Применяя теорему 3, найдем для малой
окрестности
.
Применяя теорему 3, найдем для малой
окрестности
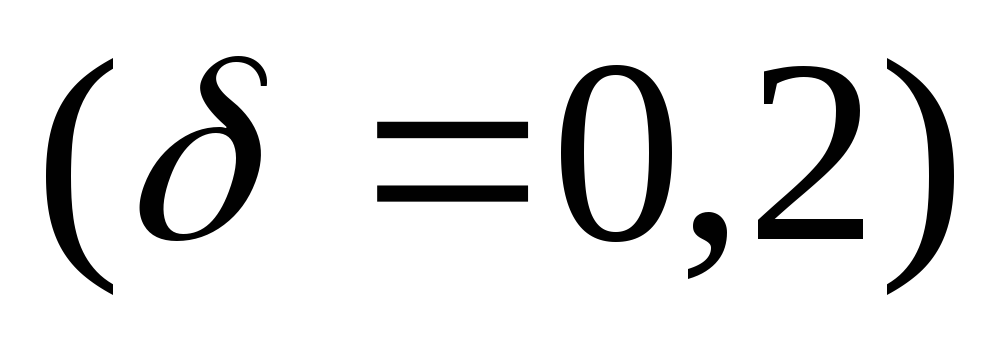 точки
точки
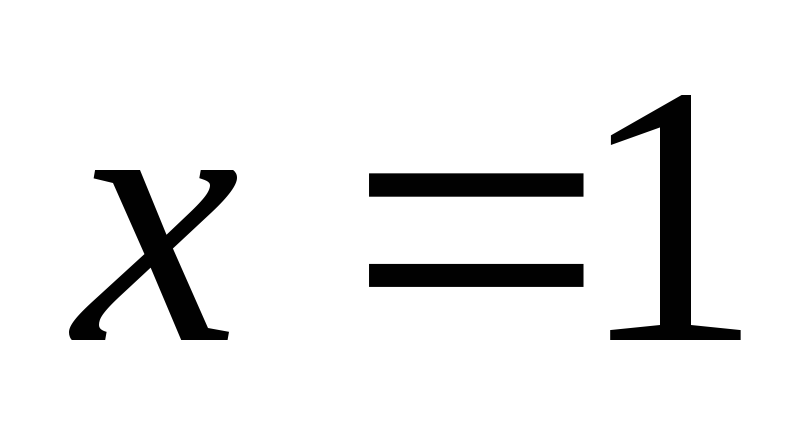 .
При
.
При
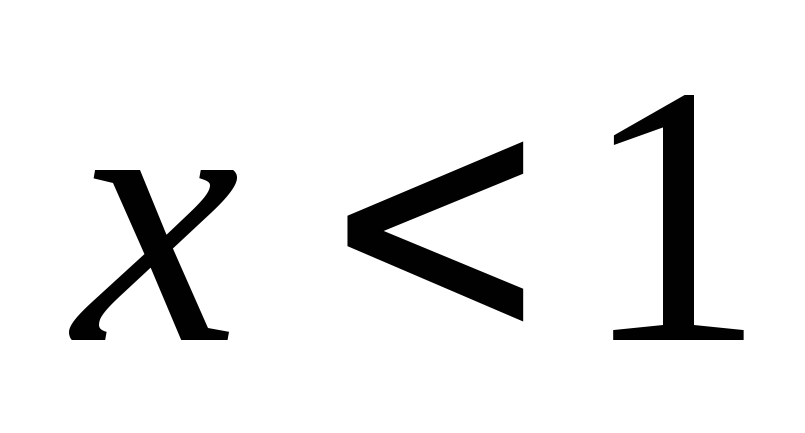 ,
,
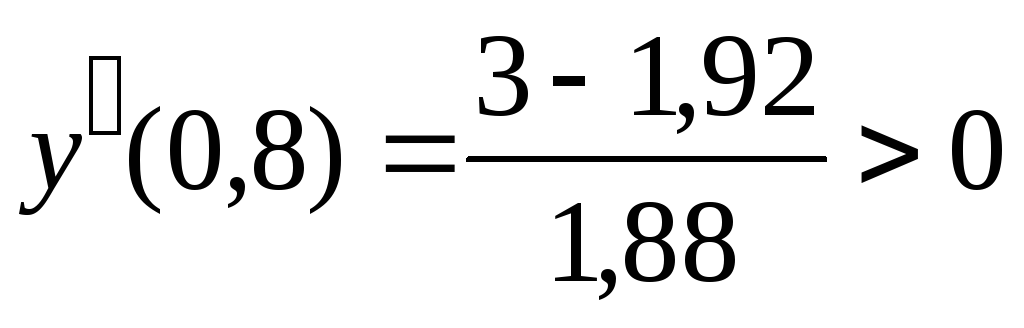 при
при
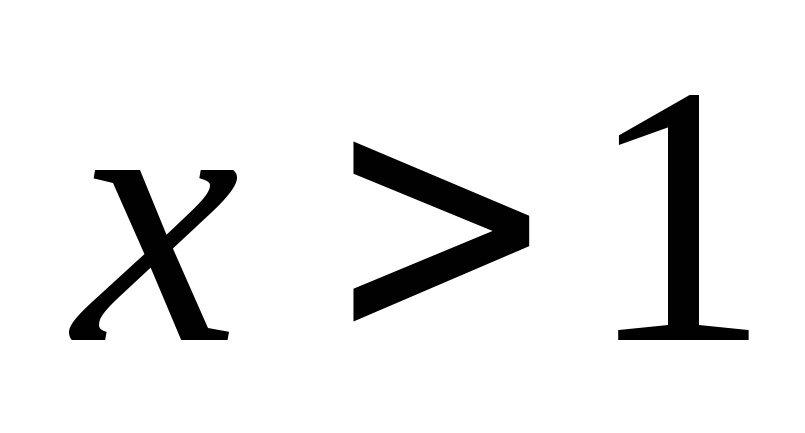 ,
,
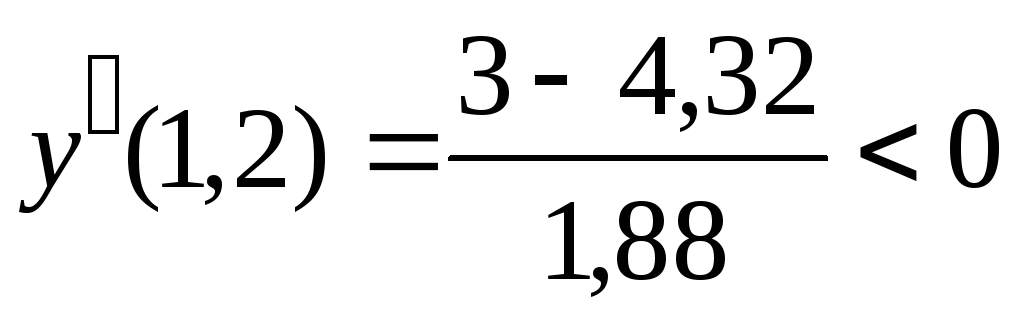 .
При
переходе через точку
.
При
переходе через точку
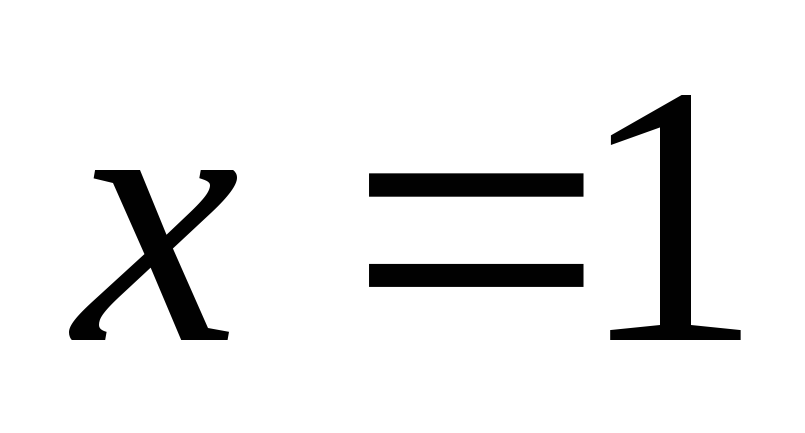
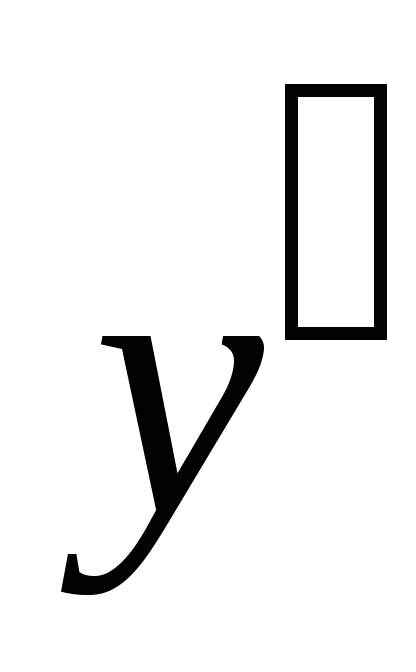 меняет знак с "+" на "-",
следовательно в точке
меняет знак с "+" на "-",
следовательно в точке
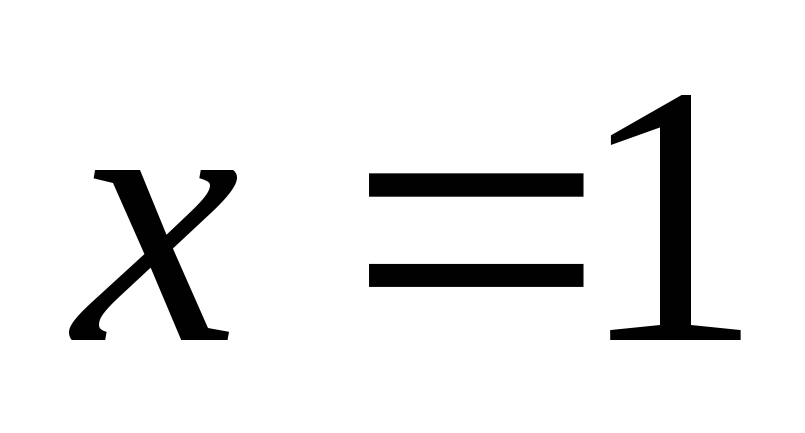 функция имеет максимум:
функция имеет максимум:
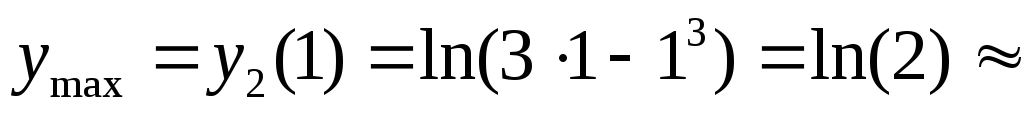
-
а) На рассматриваемом промежутке
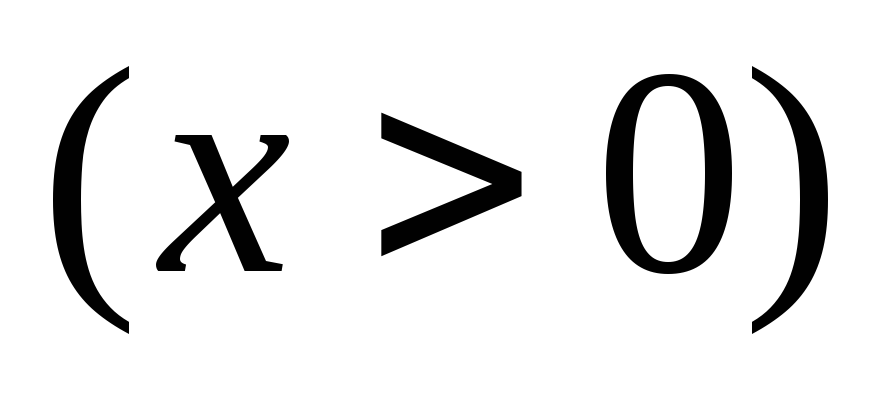 ,
в точках разрыва второго рода, исходная
функция имеет вертикальные асимптоты,
т.к.
,
в точках разрыва второго рода, исходная
функция имеет вертикальные асимптоты,
т.к.
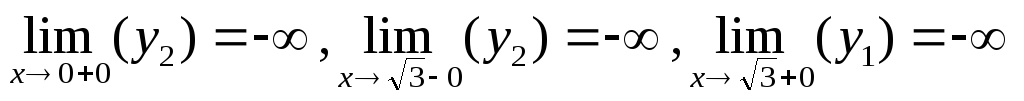 б)
наклонные асимптоты: находим
б)
наклонные асимптоты: находим
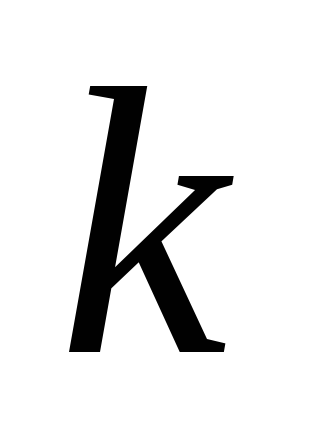 ,
применяя правило Лопиталя:
,
применяя правило Лопиталя:
 ;
Находим
;
Находим
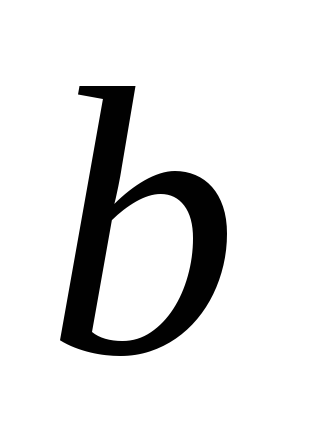 :
:
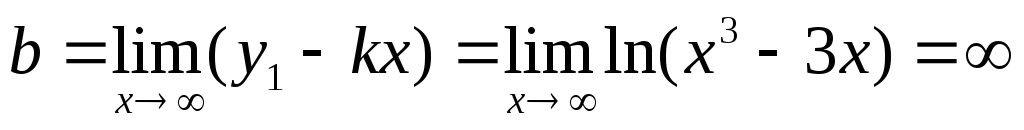 ,
т.е. не существует. Таким образом, данная
функция не имеет наклонных асимптот,
так как второй предел в (11) не существует.
Все
сказанное справедливо и для функции
,
т.е. не существует. Таким образом, данная
функция не имеет наклонных асимптот,
так как второй предел в (11) не существует.
Все
сказанное справедливо и для функции
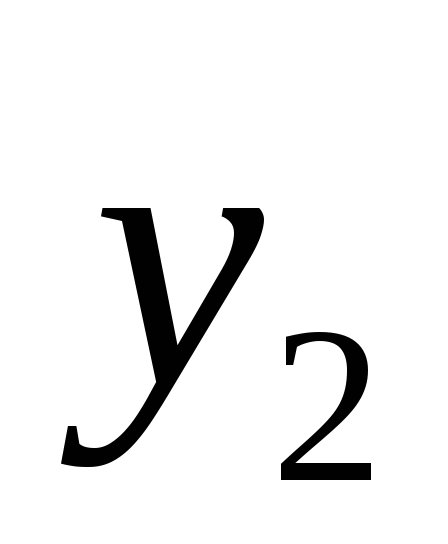 .
. -
Находим вторую производную
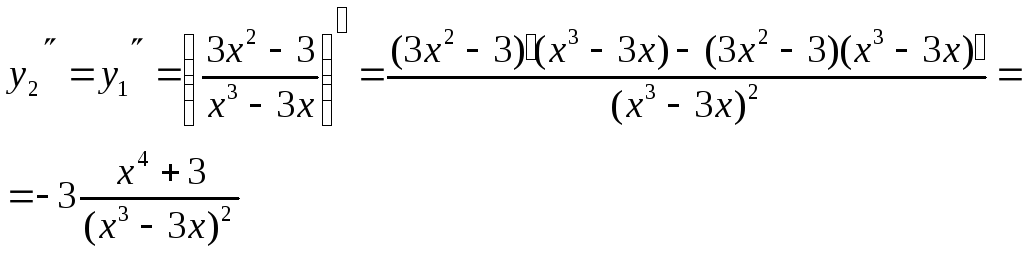 Так
как
Так
как
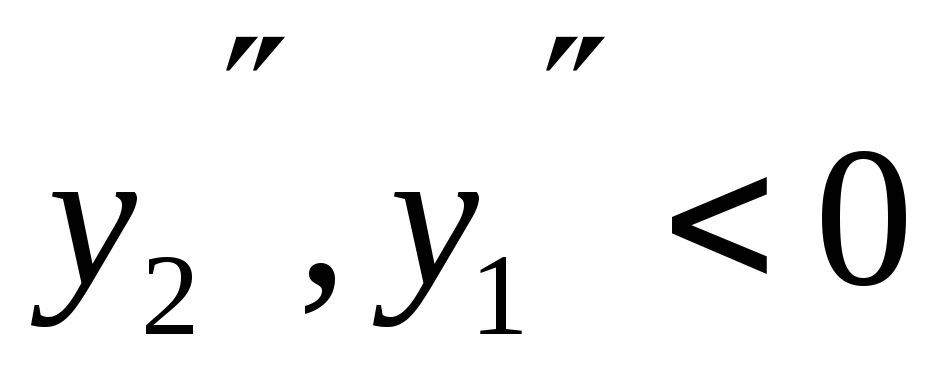 всюду в ОДЗ, то дуги данной функции на
любом интервале выпуклы.
Производные
всюду в ОДЗ, то дуги данной функции на
любом интервале выпуклы.
Производные
 и
и
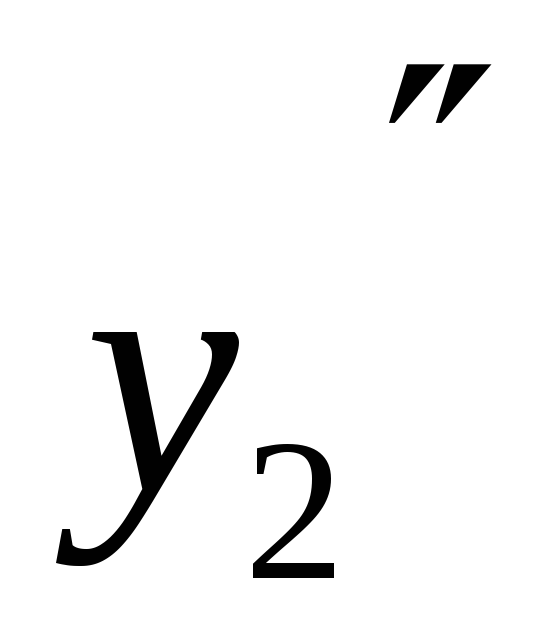 не существуют в точках:
не существуют в точках:
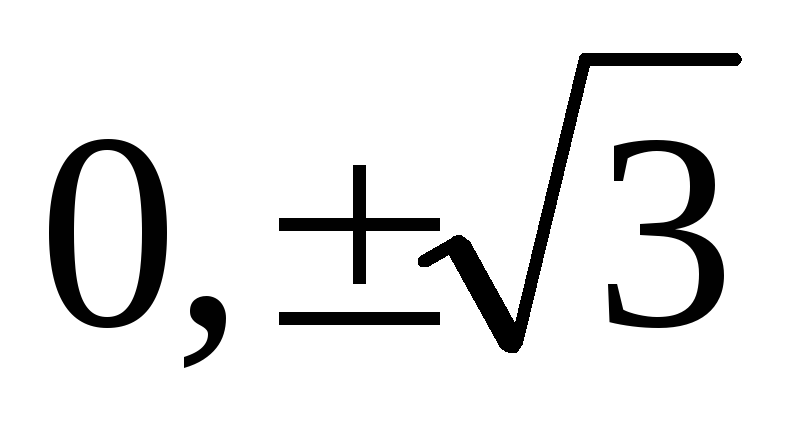 не входящих в ОДЗ и ни где не равны нулю,
следовательно данная функция
не входящих в ОДЗ и ни где не равны нулю,
следовательно данная функция
 не имеет точек перегиба.
не имеет точек перегиба. -
Составляя для удобства таблицу результатов исследования функции на интервале
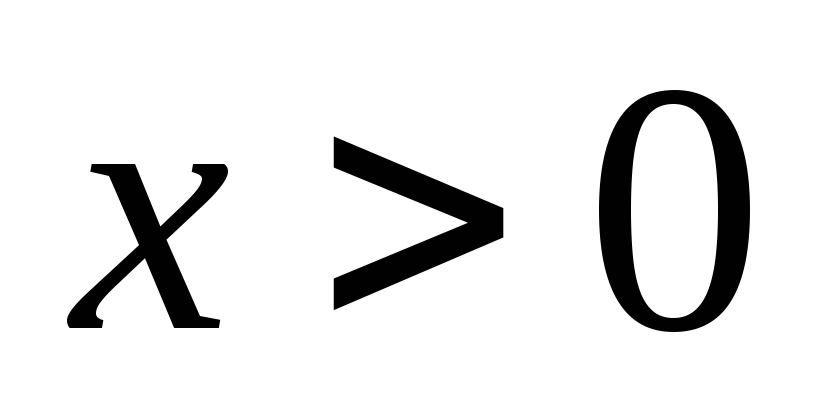 :
:
|
|
|
|
|
|
|
|
|
|
|
- |
+ |
+ |
+ |
- |
- |
+ |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
С троим
график для
троим
график для
![]() ,
затем используя симметричность графика
достраиваем его для
,
затем используя симметричность графика
достраиваем его для
![]() .
(рис. 13)
.
(рис. 13)
Рис.14
Пример
5. 1. Функция
определена при
![]() или
или
![]() ,
откуда получаем
,
откуда получаем
![]() и систему неравенств
и систему неравенств
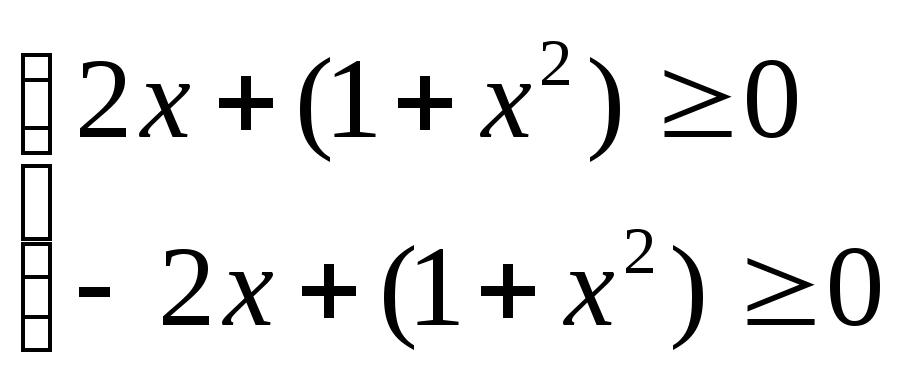 или
или
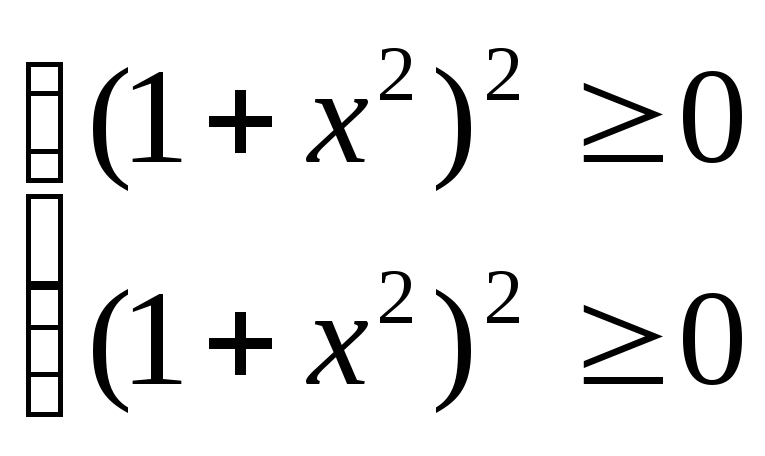 .
Так как эти неравенства справедливы
для любых
.
Так как эти неравенства справедливы
для любых
![]() ,
то функция
,
то функция
![]() определена при всех
определена при всех
![]() .
.
2.
Функция нечетная, так как
![]() .
Следовательно,
график функции
.
Следовательно,
график функции
![]() симметричен относительно начала
координат, поэтому достаточно исследовать
функцию при
симметричен относительно начала
координат, поэтому достаточно исследовать
функцию при
![]() .
Функция
.
Функция
![]() не является периодической.
не является периодической.
-
С осями координат график функции пересекается в начале координат – точке О
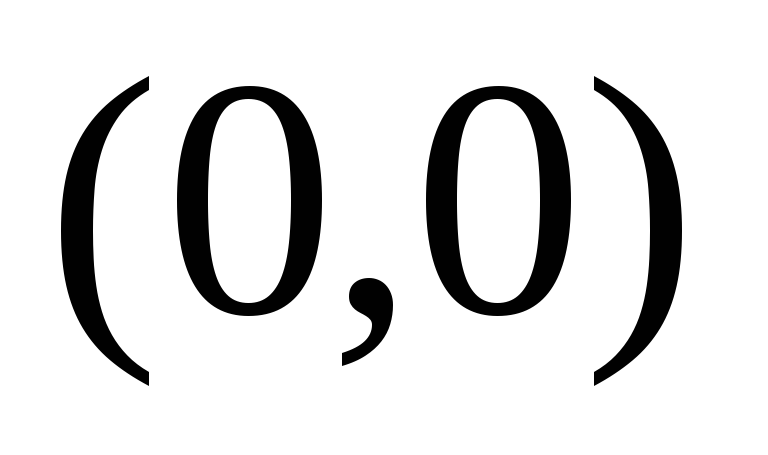 .
. -
На рассматриваемом промежутке
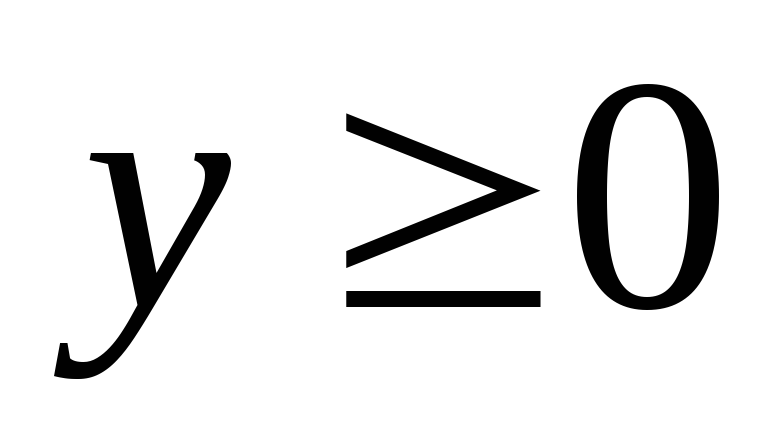 .
. -
Найдем производную:
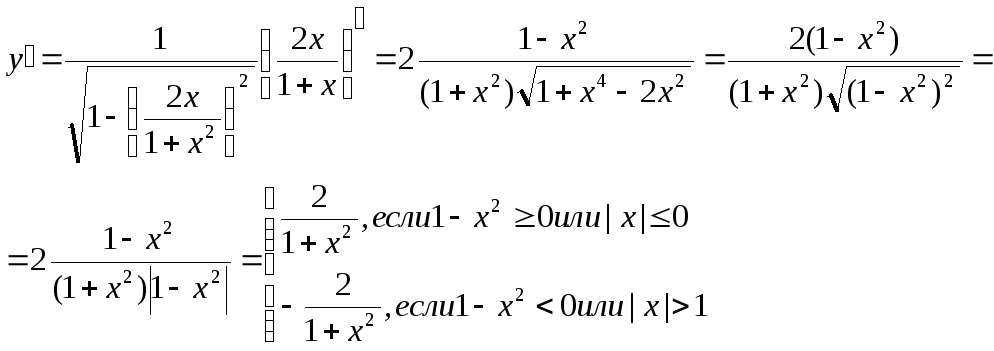 Производная
ни где не обращается в нуль и не существует
в точках
Производная
ни где не обращается в нуль и не существует
в точках
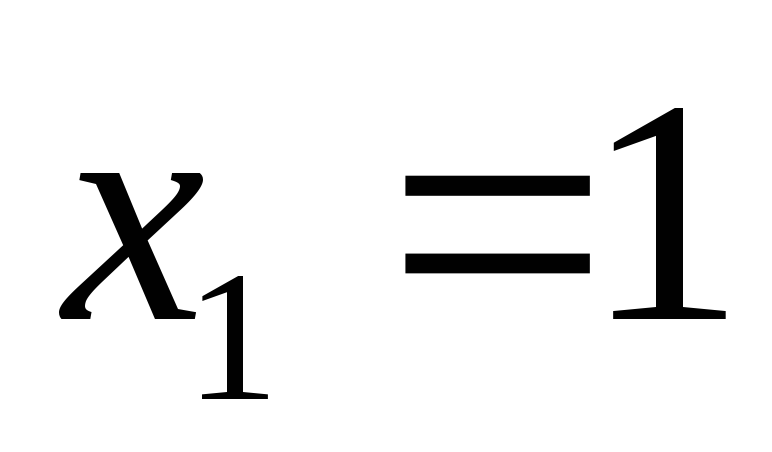 и
и
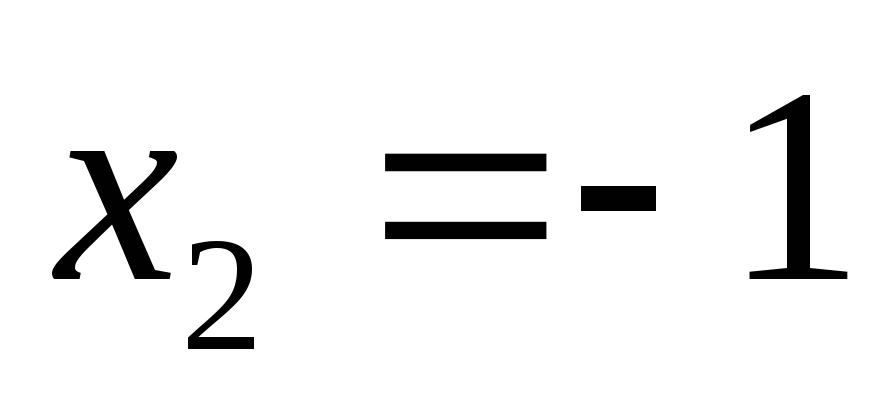 .
На
рассматриваемом отрезке подозрительном
на экстремум является точка
.
На
рассматриваемом отрезке подозрительном
на экстремум является точка
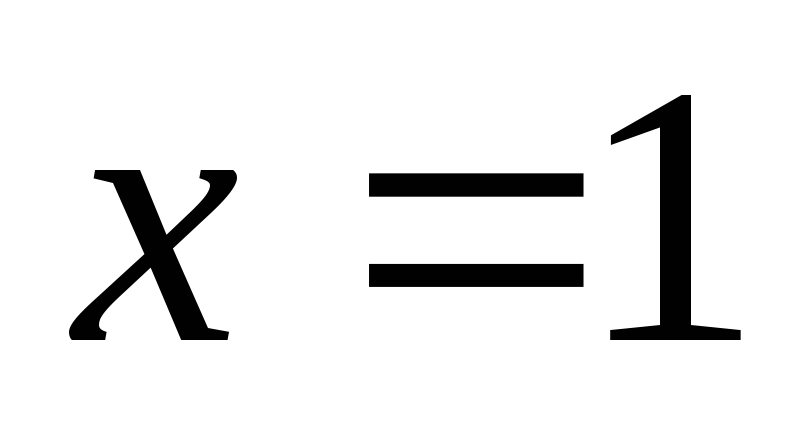 .
Используя теорему 3, получим для малой
окрестности
.
Используя теорему 3, получим для малой
окрестности
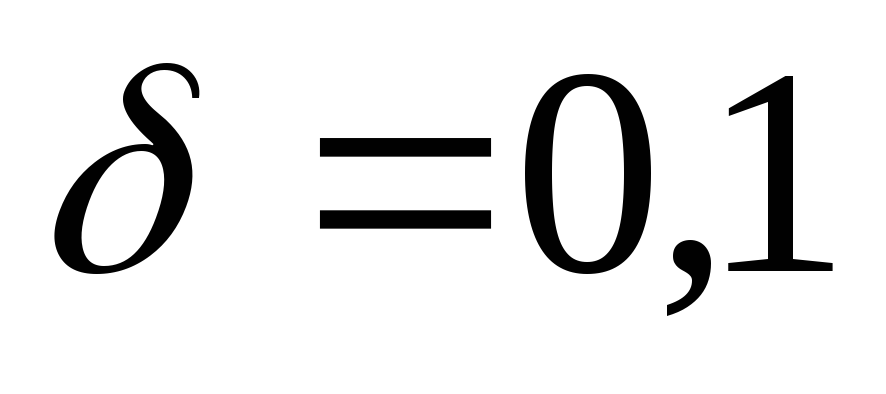 точки
точки
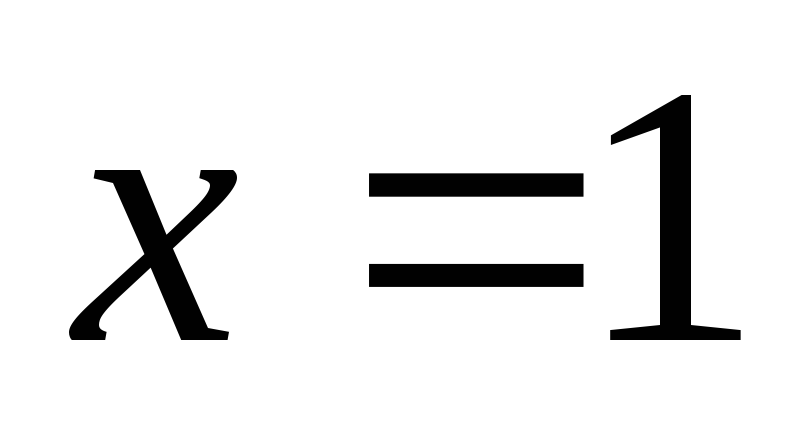 :
:
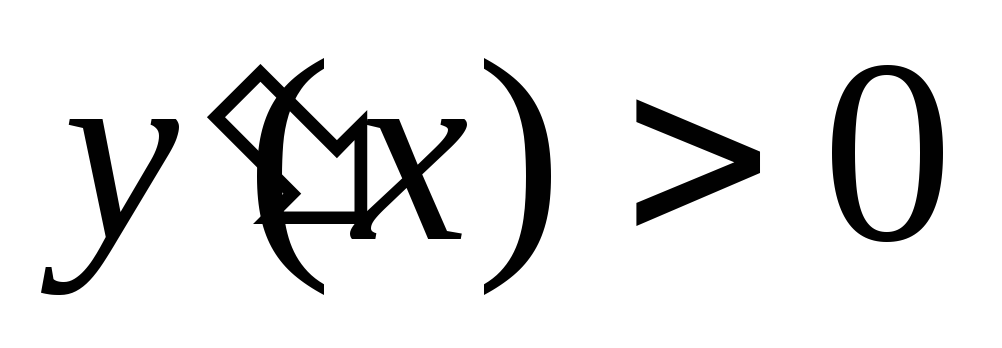 при
при
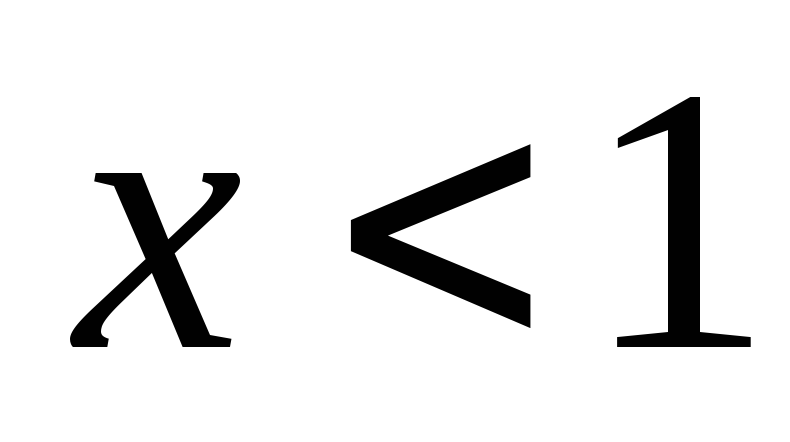 и
и
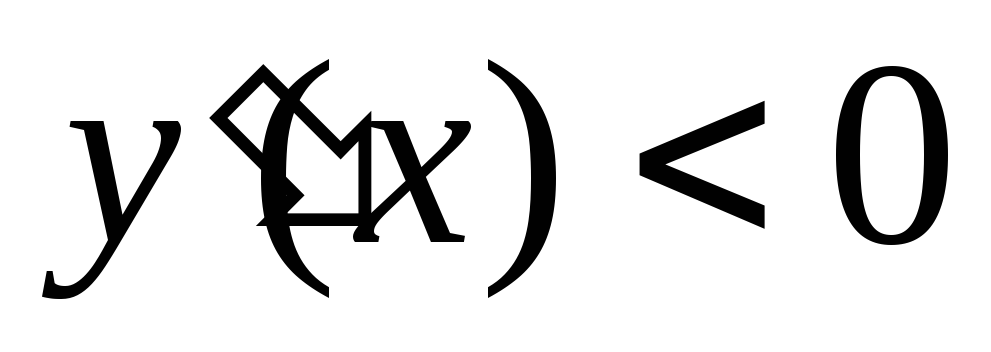 при
при
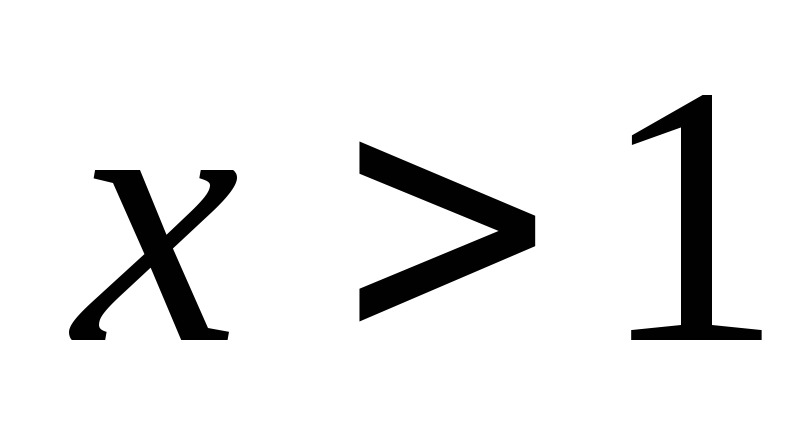 .
Так как производная
.
Так как производная
 меняет знак с "+" на "-", то в
точке
меняет знак с "+" на "-", то в
точке
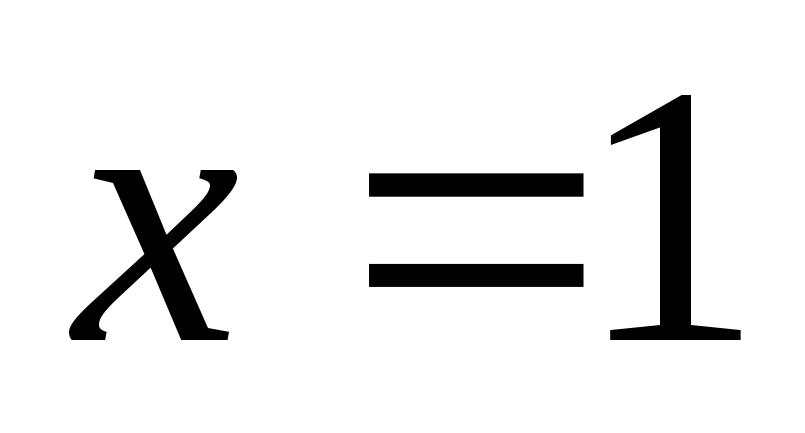 функция имеет максимум:
функция имеет максимум:
 .
Отметим,
что так как в самой точке
.
Отметим,
что так как в самой точке
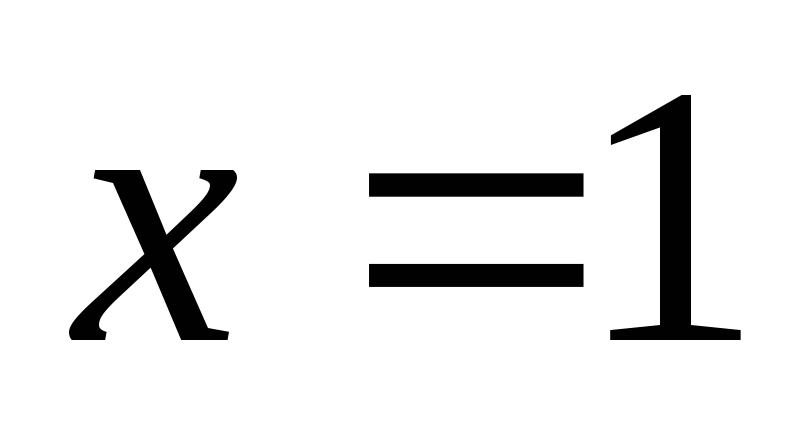
 не существует
не существует
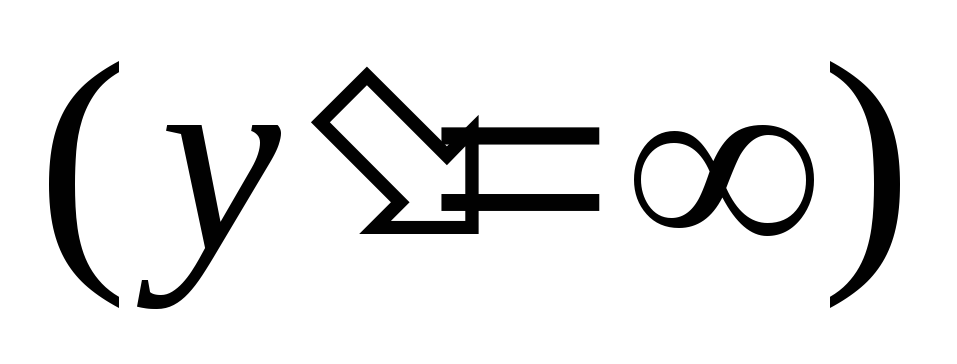 ,
в этой точке максимум острый слева от
точки
,
в этой точке максимум острый слева от
точки
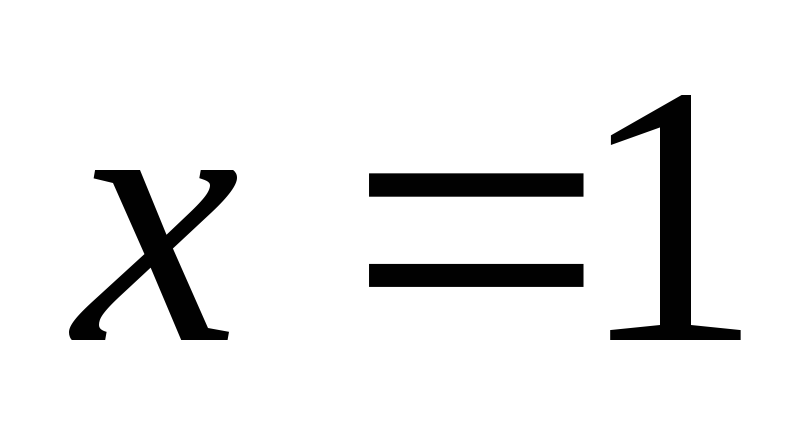 на интервале
на интервале
 ;
;
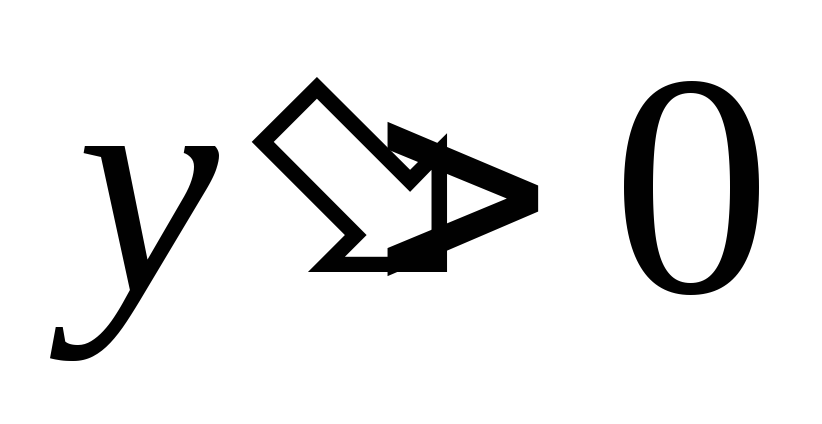 ,
и функция возрастает; Справа, на интервале
,
и функция возрастает; Справа, на интервале
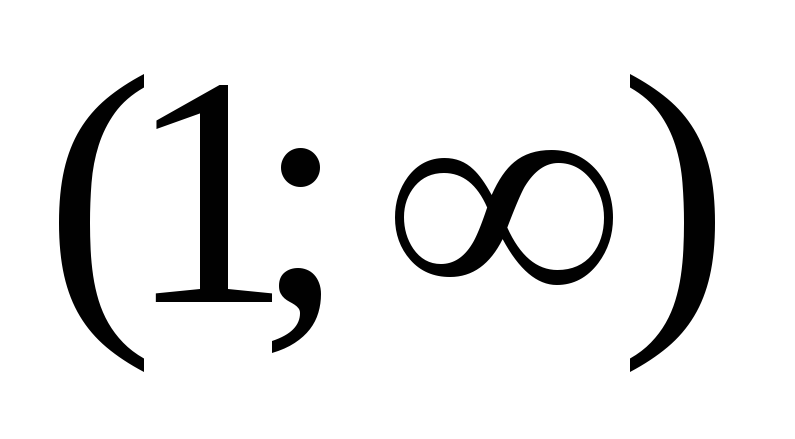 ,
,
 ,
функция убывает.
,
функция убывает. -
а) Функция не имеет вертикальных асимптот, так как нет точек разрыва второго рода. б) наклонные асимптоты:
 Таким
образом функция имеет одну асимптоту
Таким
образом функция имеет одну асимптоту
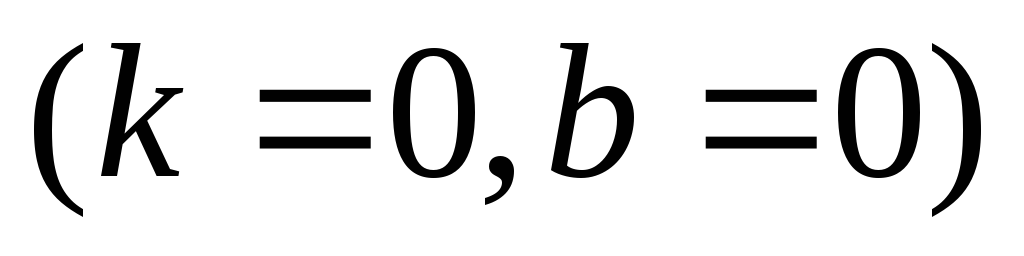 ,
которой является ось
,
которой является ось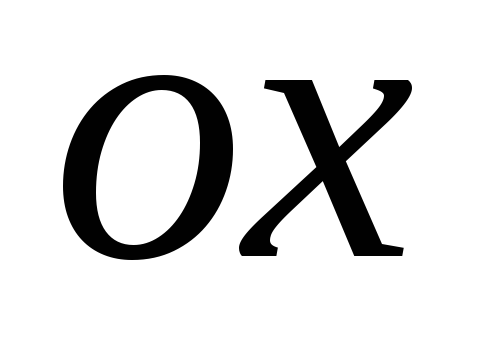 .
. -
Вычислим
 для
для
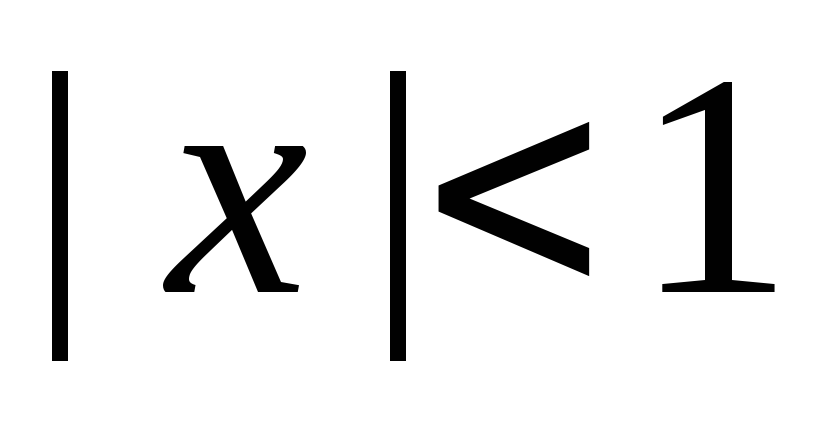 и
и
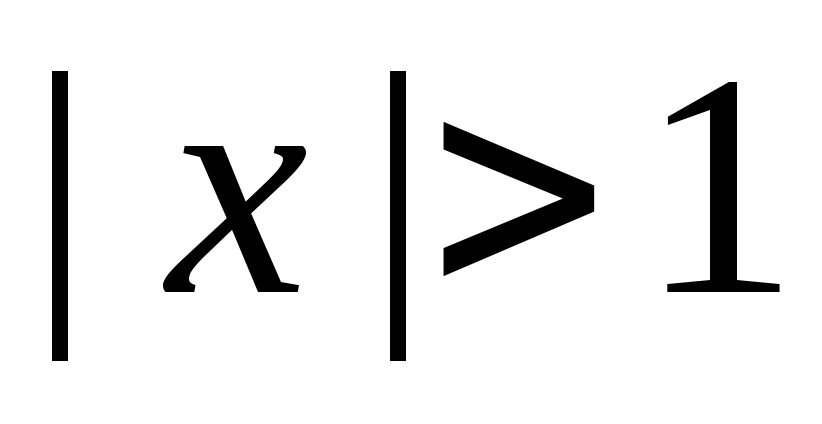 :
:
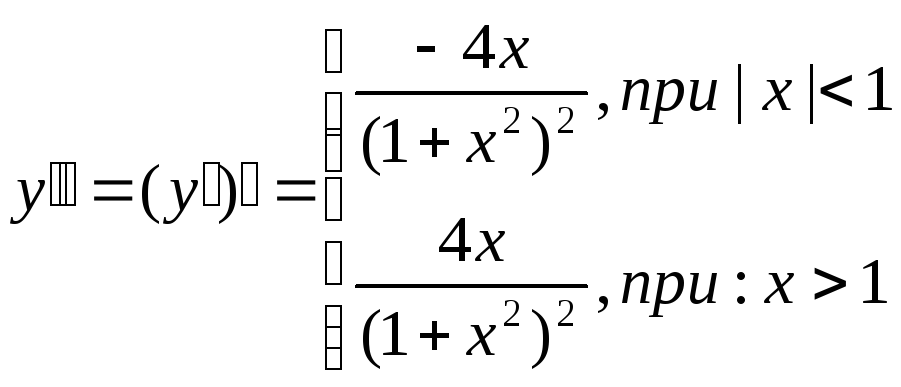
Вторая
производная равна нулю при
![]() и не существует в точках
и не существует в точках
![]() ,
так как при этих значениях не существует
,
так как при этих значениях не существует
![]() .
.
Легко
видеть, что
![]() при
при
![]() и
и
![]() при
при
![]() .
Это означает, что слева от точки
.
Это означает, что слева от точки
![]() кривая вогнута, а справа – выпукла.
Точка
кривая вогнута, а справа – выпукла.
Точка
![]() является абсциссой точки перегиба, а
так как
является абсциссой точки перегиба, а
так как
![]() ,
то точка О(0,0) является точкой перегиба.
В рассматриваемом интервале
,
то точка О(0,0) является точкой перегиба.
В рассматриваемом интервале
![]()
![]() в интервале (0,1) – здесь кривая выпукла;
в интервале (0,1) – здесь кривая выпукла;
![]() в интервале
в интервале
![]() - здесь кривая вогнута. По определению
точка
- здесь кривая вогнута. По определению
точка
![]() является абсциссой точки перегиба.
является абсциссой точки перегиба.
Так
как
![]() ,
то тогда
,
то тогда
![]() является точкой перегиба (и точкой
максимума).
является точкой перегиба (и точкой
максимума).
Сводя все результаты исследования в таблицу
|
|
|
|
|
|
|
|
0 |
+ |
|
+ |
|
|
2 |
|
Не существ. |
|
|
|
0 |
|
Не существ. |
|