Предисловие.

Цель пособия – оказать студентам помощь в изучении ими таких понятий математики как предел и производная, а так же в освоении и применении методов, используемых при исследовании функций одного переменного, базирующихся на этих понятиях. При этом круг рассматриваемых вопросов не выходит за пределы программы, по существу он определяется тематикой типовых расчетов.

В пособии приводятся необходимые теоретические сведения и подробные решения типовых примеров.

Данное пособие ориентированно на студентов экономических групп специальностей 0605 – «Бухгалтерский учет и аудит»; 0719 – «Информационные системы в экономике».

При исследовании графиков функций при неограниченном возрастании (по абсолютной величине) абсциссы или ординаты переменной точки кривой важным является случай, когда исследуемая кривая при удалении ее переменной точки в бесконечность неограниченно приближается к некоторой прямой А.

Определение 6. Прямая А называется асимптотой кривой, если расстояние от переменной точки М кривой до этой прямой при удалении точки М в бесконечность стремится к нулю. Различают асимптоты вертикальные и наклонные.

Определение 7. Прямая называется вертикальной асимптотой графика функций , если справедливо хотя бы одно из нижеследующих выражений:

(10)

Из определения 7 следует, что вертикальные асимптоты следует искать как такие значения , при приближении к которым аргумента , функция стремится к бесконечности. Обычно это точки разрыва второго рода функции , если их нет, то вертикальные асимптоты отсутствуют.

Теорема 7. Прямая тогда и только тогда является наклонной асимптотой графика функций при , когда

(11)

Замечания. Иногда наклонные асимптоты называют левыми, если в (11) и правыми, если . Если хотя бы один из пределов (11) не существует, то функция не имеет наклонной асимптоты.

Пример. Найти асимптоты кривой

Решение. а) Вертикальная асимптота: , так как при ,

б) Наклонная асимптота

,

,

- наклонная асимптота.

При получаем то же выражение, т.е. наклонная асимптота одна.

Пример. Найти асимптоты кривой

Решение: а) Очевидно кривая не имеет вертикальных асимптот, так как только при

б) Найдем и для наклонных асимптот.

,

,

Если , то получим и .

Таким образом, кривая имеет две наклонные асимптоты.

, при

и , при .

3. Полное исследование функции.

   Приведенные выше теоретические сведения по определению интервалов монотонность функции, ее экстремумов, интервалов выпуклости и вогнутости графика функции, его точек перегиба и асимптот позволяют провести полное исследование функции и построить ее график, дающий представление о характерных свойствах и особенностях исследуемой функции. Полное исследование функции проводится по следующему примерному плану:

1. Находится область допустимых значений (ОДЗ) функции.

2. Выясняется, является ли функция четной, нечетной, периодической или общего вида.

3. Определяются точки пересечения с осями координат графика функции, находятся ее нули и точки разрыва.

4. Находятся интервалы знакопостоянства функции.

5. Находятся критические точки, интервалы возрастания, убывания и точки экстремума, а так же характер экстремума в каждой точке.

6. Находятся вертикальные и наклонные асимптоты графика функции.

7. Определяются интервалы выпуклости, вогнутости и точки перегиба графика функции.

8. Для большей точности графика иногда строятся и отдельные точки графика.

9. Строится график функции.

Ниже приводятся примеры полного исследования и построения графиков различных видов функций. По ходу исследования приводятся при необходимости соответствующие пояснения.

Пример 1. Исследовать функцию и построить ее график.

Решение. 1.Функция определена всюду, кроме точек

и , поэтому ее ОДЗ включает интервалы

2. Функция нечетная, так как , следовательно, график функции симметричен относительно начала координат. Функция не периодическая.

3. Точки пересечения графика функции с осями координат: с осью при ; с осью при , т.е. кривая проходит через начало координат.

4. Для определения интервалов знакопостоянства построим кривую знаков (рис.6)

Рис.6

Из рис. 6 следует, что данная функция:

положительна в интервалах и

отрицательна в интервалах

3. Для нахождения критических точек вычислим производную :

Производная равна нулю в точках и и не существует в точках , . Так как точки и не входят в ОДЗ функции, то критическими точками не являются. "Подозрительными" на экстремум являются точки и . С помощью первого достаточного признака экстремума (теорема 3.) определим существование и характер экстремумов в этих точках, вычисляя знак в малой окрестности точек и

а) для

В силу теоремы 3, в точке функция имеет максимум.

б) Для

так как производная меняет знак с " - " на "+" при переходе через точку , то в этой точке функция имеет минимум:

Кривая знаков производной имеет вид (см. рис. 7):

Рис.7.

Из рис. Следует, что функция возрастает на интервалах и убывает на интервалах

3. Асимптоты.

а) Очевидно, что при и , поэтому и вертикальные асимптоты.

б) ,

. - наклонная асимптота.

3. Для нахождения интервалов выпуклости вогнутости вычислим и рассмотрим кривую знаков (см. рис. 8)

рис. 8.

Вторая производная равна нулю при и не существует при и (точки не входят в ОДЗ).

Т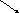ак как при кривая выпукла, а при - выгнута, то график функции выпуклый на интервалах и выгнутый на интервалах , что отмечено знаками и в таблице, которую удобно использовать при построении графика, в этой таблице знаками и отмечено возрастание, и убывание функции

	-	-	+	-	+	+

Из таблицы следует, что меняет знак при переходе через точку , но тогда по теореме 6 эта точка является абсциссой точки перегиба.

8. Учитывая результаты исследования, строим график заданной функции (рис. 9.)

Рис. 9.

Первая производная равна нулю при и не существует в точках , которые вне ОДЗ, и критическими не являются. Для нахождения характера экстремума используем второй достаточный признак (см. теорему 4.)

В критической точке .

;

отсюда следует, что при четном и в таких точках функция имеет минимум; при нечетном , и в таких точках функция имеет максимум.

На рассматриваемом отрезке в точках и функция имеет минимум.

, а в точке - максимум.

.

Интервалы возрастания и убывания функции найдем по закону , который определяется знаком (числителя):

на интервалах , следовательно, на этих интервалах функция возрастает;

на интервалах , следовательно, на этих интервалах функция убывает.

6. а) Вертикальные асимптоты проходят через точки разрыва второго рода, их уравнения

,

на рассматриваемом отрезке и .

б) Наклонных асимптот функция не имеет, так как второй из пределов (11) не существует.

6. Вторая производная , знак которой определяется знаком (знаменателя), на рассматриваемом промежутке положительна при и и отрицательна при . Следовательно, кривая вогнута на интервалах и , и выпукла на интервале . Вторая производная меняет знак при переходе через точки , которые в ОДЗ заданной функции не входят и поэтому абсциссами точек перегиба не являются, т. е. функция точек перегиба не имеет.

7. На основе выводов по каждому пункту составляем для удобства построения графика таблицу. Строим график (рис. 11) для отрезка и продлеваем его на всю ось , используя периодичность заданной функции.

	1	+	-	-1	-	+	1
	0			0			0
	1			-1			1

Рис.11

Пример 4. Исследовать функцию и построить ее график.

Решение. 1.ОДЗ находим из неравенства Так как по определению модуля:

,

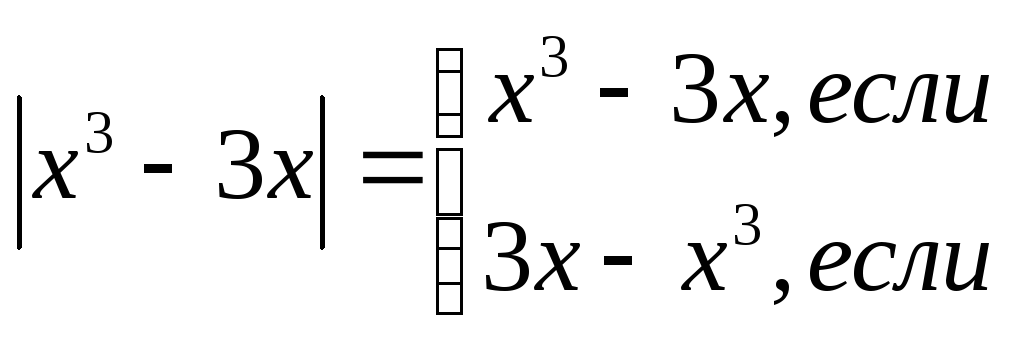
то, очевидно, ОДЗ данной функции является вся числовая ось за исключением точек, где , т.е. точек: и .

Эти точки разбивают числовую ось на интервалы, в которых данная функция может быть выражена (принимая во внимание определение модуля) следующими аналитическими уравнениями:

а) если и

б) если и

Отметим это на рисунке 12.

y₂

y₁

y₂

y₁

0

_x

Рис. 12.