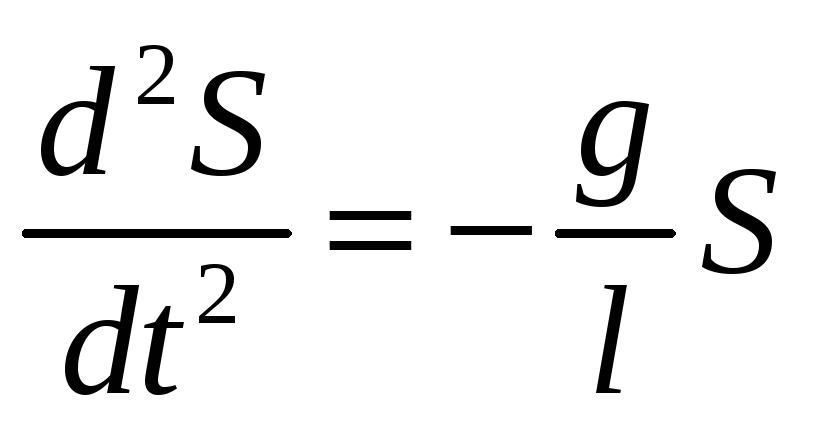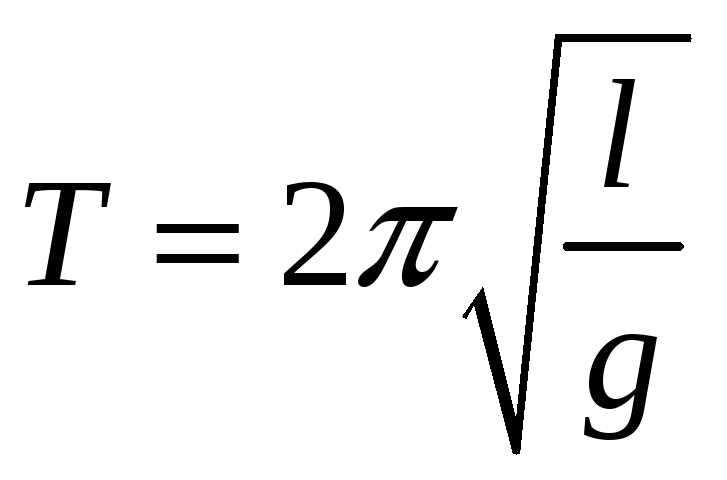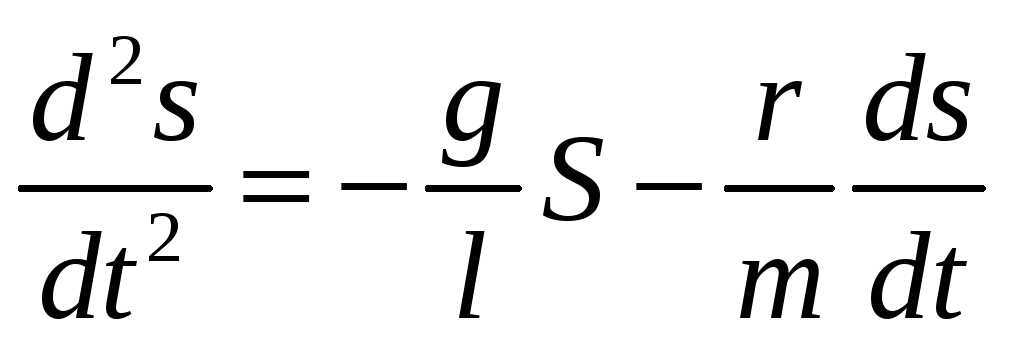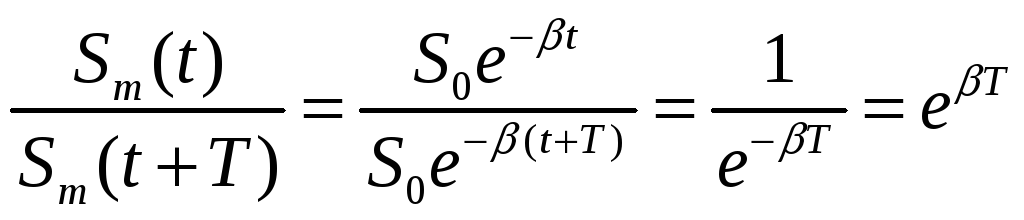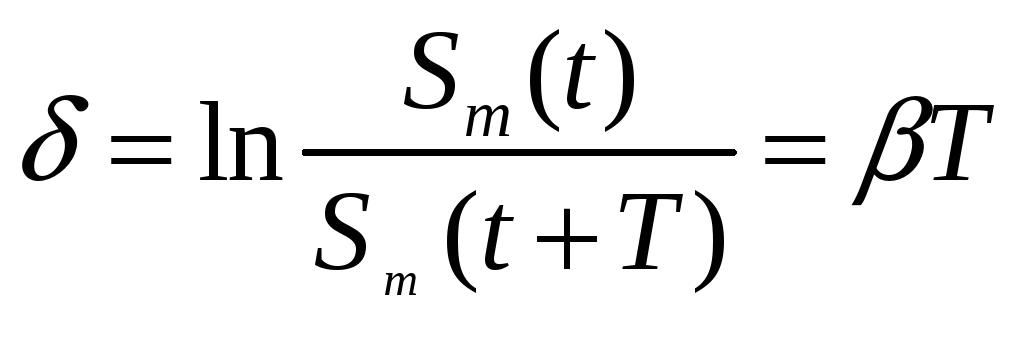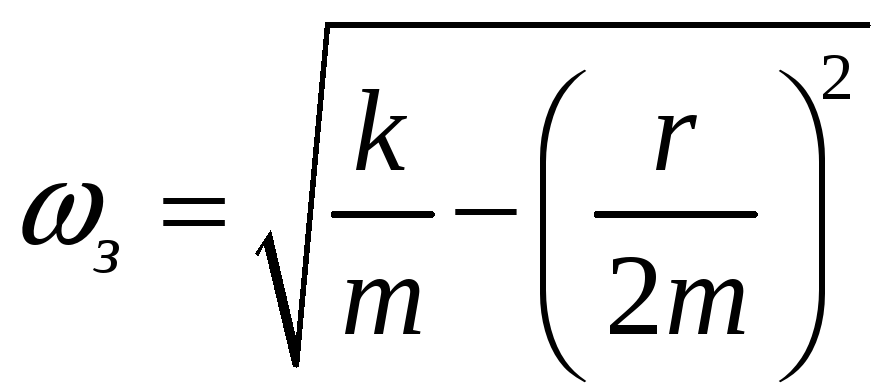5. Контрольні питання

1. Як побудований кожний з вимірювальних приладів (штангенциркуль, мікрометр, аналітичні та торсійні ваги)?

2. Що таке штангенциркуль, ноніус і принцип вимірювання довжини тіл з їх допомогою?

3. Будова мікрометра та принцип вимірювання довжини з його допомогою.

4. Яка точність вимірювання штангенциркулем, мікрометром і технічними вагами, що використовуються в роботі?

5. Які межі вимірювання даними приладами?

6. Як визначається абсолютна похибка окремих прямих вимірювань?

7. Як оцінити похибку непрямих вимірювань?

8. Чи співпадають між собою – в межах похибок – дані вимірювання одного і того ж тіла, зроблені на різних ділянках?

9. Як можна встановити, що відхилення форми вимірюваного тіла від правильної носить випадковий, або, навпаки, регулярний характер?

6. Література

1.В.М. Авдусь. Практикум по загальній фізиці. М.– 1971.– С. 6-30.

2.В.Є.Винниченко. Фізичний практикум. Київ: „Радянська школа”.– 1959.

3.Эссаулова И.А. и др. Руководство к лабораторным работам по медицинской и биологической физике.М.: „Высшая школа”.– 1987.

Лабораторна робота №2

Визначення прискорення сили земного тяжіння

за допомогою математичного маятника та

декремента загасання коливань маятника

Мета роботи: Ознайомитися з власними коливаннями математичного маятника. Визначити період коливань математичного маятника, прискорення сили земного тяжіння, логарифмічний декремент загасання та коефіцієнт загасання.

Необхідні прилади і матеріали: математичний маятник на штативі, секундомір, вимірювальна лінійка.

1. Короткі теоретичні відомості

Багато процесів в природі являються періодичними (зміна пори року, артеріального тиску, тощо). Періодичність властива процесам, що відбуваються в біологічних системах (біоритми). Більшість із з них можна розглядати як коливні. Коливним називається рух, що повторюється через певний проміжок часу. Цей проміжок часу, протягом якого повторюються значення всіх фізичних величин, що характеризують коливний рух, називається періодом. За один період здійснюється одне повне коливання. Коливний рух, що відбувається без дії зовнішніх сил, тобто під дією тільки внутрішніх сил системи, називаються вільними коливаннями. Для медиків і біологів важливі поздовжні коливання середовища – звук, інфразвук та ультразвук. Їхні фізичні властивості широко використовується в медицині.

Найзручнішим і простим об'єктом для дослідження коливних процесів є механічна система з одним ступенем вільності , тобто така система, положення якої в просторі у будь-який момент часу повністю визначається одним числом – координатою. Класичним прикладом такої системи є математичний маятник. Математичний маятник – це абстракція: на невагомій нерозтяжній нитці висить матеріальна точка (тіло, що має масу, але не має розмірів). Центр ваги такої системи співпадатиме з центром ваги матеріальної точки. Практично такий маятник створити неможливо, але маленька кулька, підвішена на нитці, розміри якої у багато разів більші за розміри кульки, за своїми властивостями близька до математичного. Якщо таку систему вивести з положення рівноваги на малий кут, вона буде здійснювати гармонічні коливання. Коливання називаються гармонічними, якщо вони описуються рівнянням

(1)

Тут x – відхилення від положення рівноваги, t – час, ω –кутова частота, А – амплітуда, – початкова фаза. Весь вираз () називається фазою коливання. Кутова частота пов'язана з циклічною частотою  (числом коливань в одиницю часу) і періодом коливань Т формулами і . Одиниця вимірювання кутової частоти в системі одиниць СІ – радіани в секунду (рад/с).

Вільне коливання системи є простими гармонічними, якщо повертаюча сила хоча б в першому наближенні (при малих зсувах) пропорційна зсуву, тобто є квазіпружною силою. Тоді диференціальне рівняння руху може бути представлено у вигляді

(2)

де m визначає інерцію системи, а (–kx) є повертаюча сила (в узагальненому значенні). Частота власних коливань зв’язана з коефіцієнтами рівняння (2):

(3)

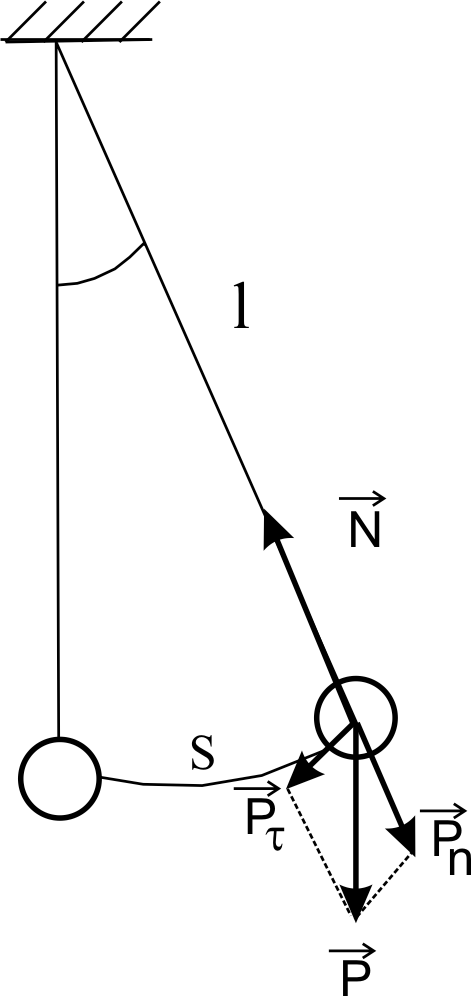
Зупинимось більш детально на розгляді коливань математичного маятника. Рівняння руху коливань математичного маятника - це залежність дугового зсуву маятника S від часу t (рис.1).

Для отримання закону коливання маятника використовуємо рівняння руху Ньютона:

.

(4)

На кульку маятника діє сила тяжіння і сила натягу нитки .

Рис.1. Математичний маятник.

Виведемо маятник з положення рівноваги на малий кут . Розкладемо силу на дві складові і . Сила забезпечує коливання маятника. Модуль цієї сили рівний . Використовуючи закон (4), отримаємо . Оскільки 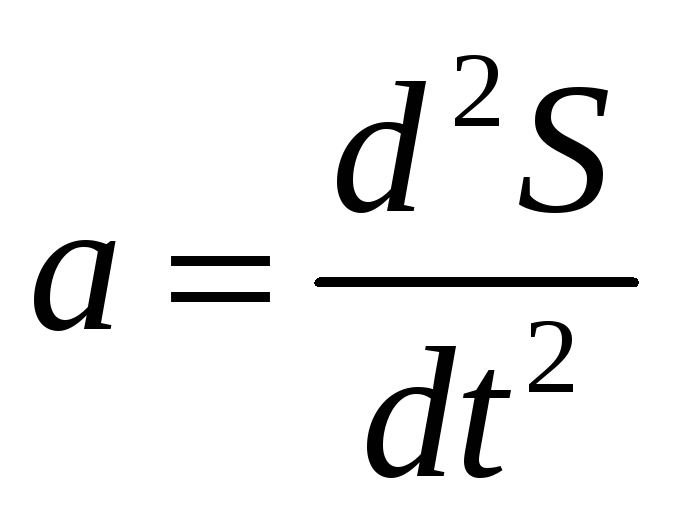, а , то:

(5)

Це і є диференціальне рівняння гармонічного коливання. Тут , -власна циклічна частота гармонічного коливання. Розв’язок цього рівняння дає закон коливань математичного маятника , де - амплітуда коливань (максимальне зміщення маятника від положення рівноваги). Знаючи частоту , можна обчислити період (час одного повного коливання) власних коливань маятника Т:

(6)

Залежність (6) дозволяє визначити прискорення вільного падіння в даному місці Землі за відомим періодом коливань.

Коливання в реальних системах ніколи не відбуваються згідно рівняння (5): у них завжди діють дисипативні сили, що перетворюють механічну енергію на теплову. Відбувається загасання коливань і в цьому випадку коливання вже не будуть гармонічними, оскільки в них змінюється амплітуда коливань і частота, що в свою чергу приводить до зміни періоду коливань. Простим, з математичної точки зору, прикладом таких сил є сили опору. При дії сил опору амплітуда і швидкість коливального руху зменшуються. Практично, найбільший інтерес представляють випадки коливань з невеликими швидкостями, при яких сила опору пропорційна швидкості :

,

(7)

де - коефіцієнт опору. В цьому випадку рівняння руху маятника запишеться в наступному виді:

(8)

тобто, крім сили на тіло діє сила опору . Розв’язком цього рівняння є функція виду:

(9)

або вводячи позначення , де 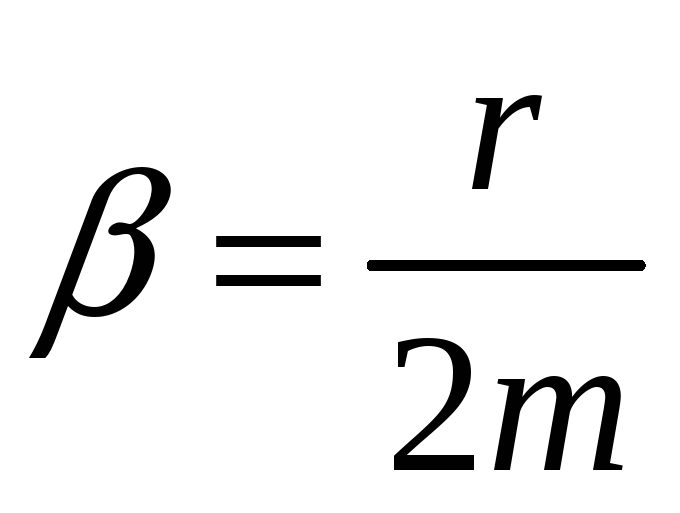отримаємо

(10)

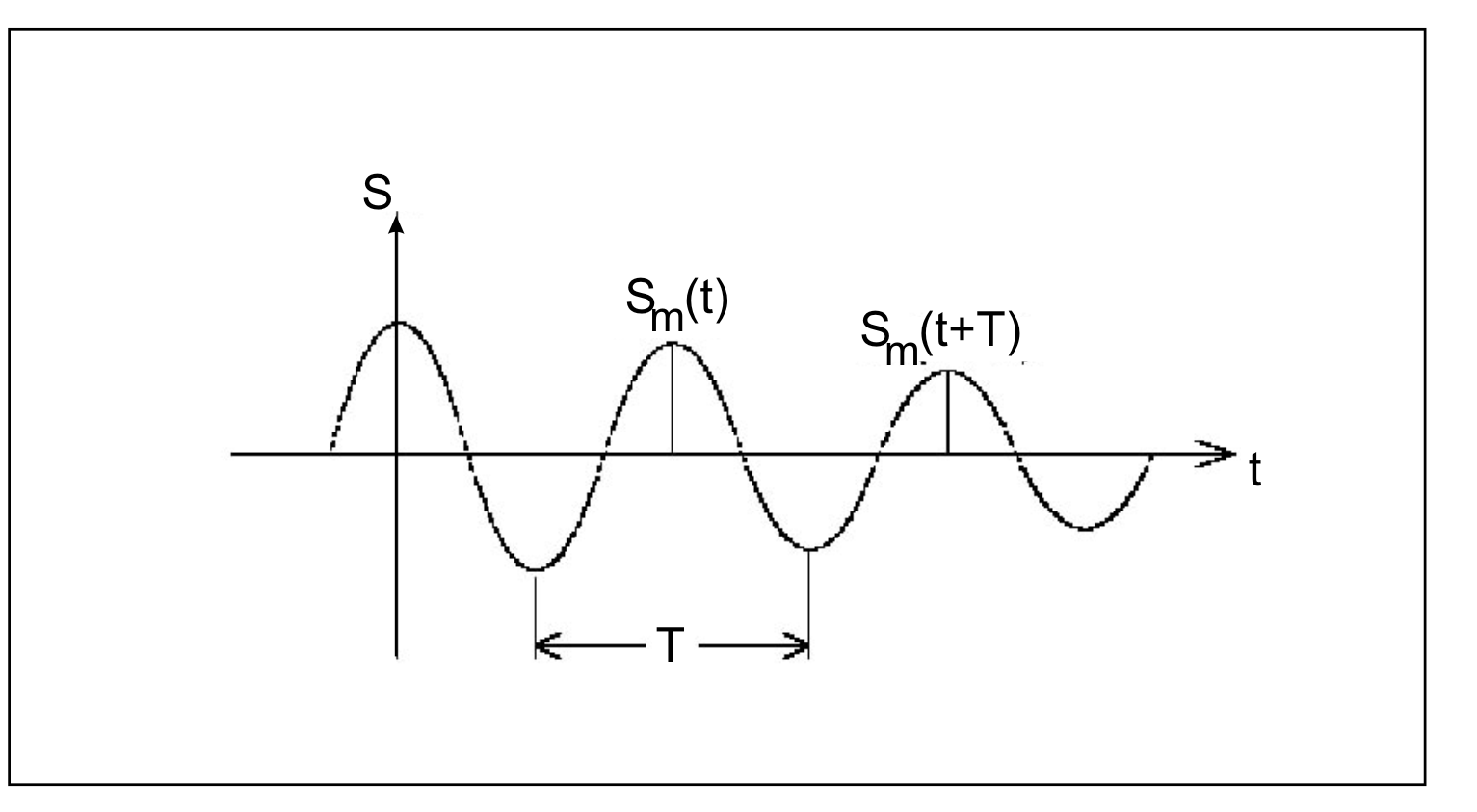
З рівняння (10) слідує, що амплітуда коливань зменшується з часом згідно експоненціального закону (рис.2).

Рис.2. Залежність ампдітуди коливань від часу при загасаючих коливаннях.

Відношення амплітуд коливань, що за часом віддалені один від одного на період, називається декрементом загасання.

(11)

Натуральний логарифм цього відношення називається логарифмічним декрементом загасання:

(12)

тут - коефіцієнт загасання. Із (12) знаходимо зв’язок між величинами і :

(13)

Логарифмічний декремент загасання характеризує швидкість зменшення амплітуди і залежить від коефіцієнта опору r середовища. Формулу (9) можемо записати в іншому виді:

(9а)

З формули (9а) видно, що величина, зворотня декременту загасання (точніше, ціла частина цього числа), рівна кількості коливань, за яку амплітуда зменшиться в =2,718 раз.

Для загасаючих коливань із розв’язку рівняння (9) отримаємо значення частоти коливань:

(14)

або враховуючи , :

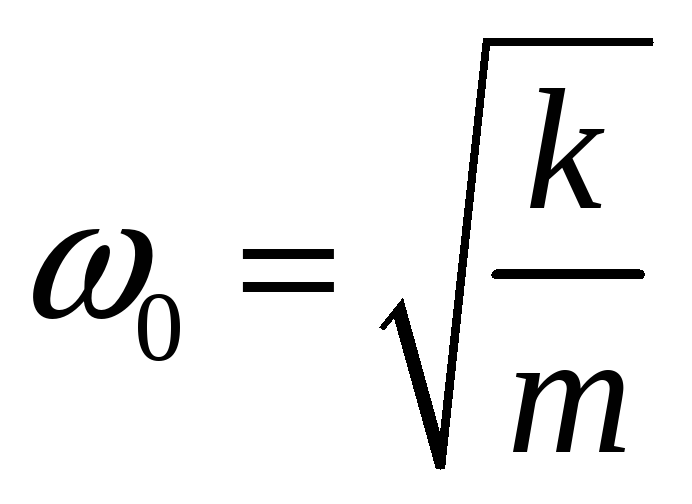(15)

Таким чином, частота вільних коливань системи з тертям нижча за частоту коливань тієї ж системи без врахування тертя.

Інколи коефіцієнт загасання співвідносять не періоду T, а часу t коливань. Тоді логарифмічний декремент загасання можна визначити, знаючи значення амплітуди коливань і у які-небудь два моменти часу t₁ і t₂:

(16)
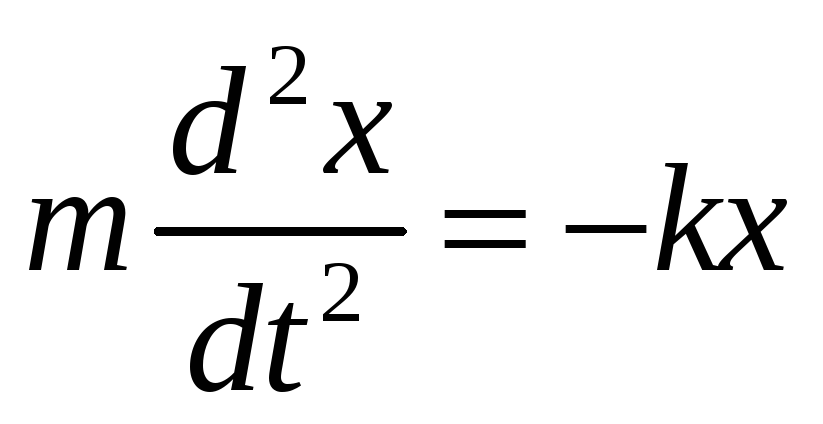
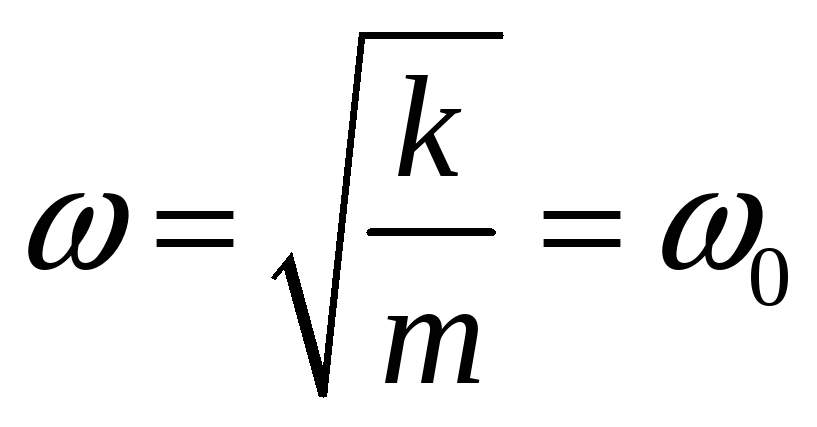
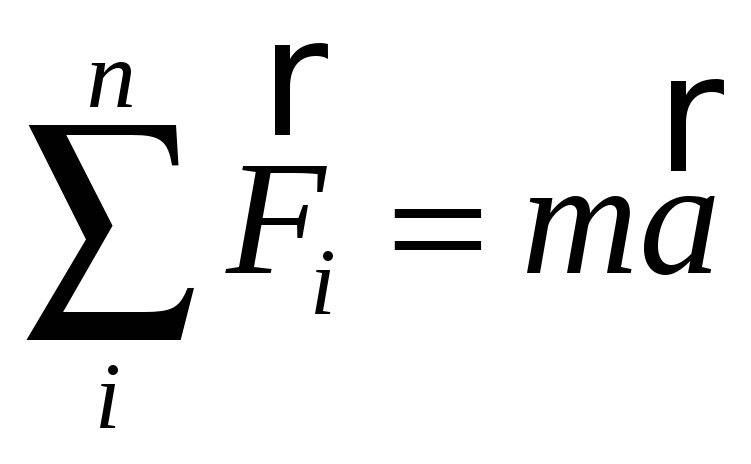