4. Парабола

Дадим общее определение рассмотренных линий: геометрическое место точек, для которых отношение расстояний до фокуса и до соответствующей директрисы является величиной постоянной, равной ε, есть эллипс, если ε < 1, и гипербола, ε > 1.

Что представляет собой геометрическое место точек, определенное аналогичным образом при условии, что ε = 1?

Параболой называется геометрическое место точек, равноудаленных от одной точки, называемой фокусом, и от прямой, называемой директрисой и не проходящей через фокус.

Д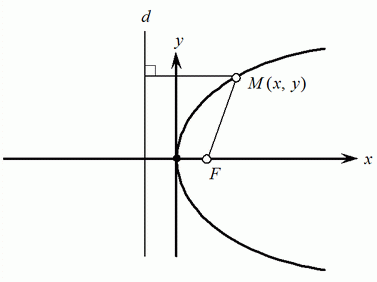ля вывода уравнения параболы ведем на плоскости прямоугольную систему координат так, чтобы ось абсцисс проходила через фокус перпендикулярно директрисе, и будем считать положительным направлением направление от директрисы к фокусу. Начало координат расположим посередине между фокусом и директрисой. В этой системе координат фокус , а директриса задается уравнением .

Выведем уравнение параболы в выбранной системе координат.

Пусть М – произвольная точка параболы, , d – расстояние от М до директрисы, р – расстояние от фокуса до директрисы. Величину р называют параметром параболы. Точка М будет лежать на данной параболе в том и только том случае, когда : .

Обозначим через Q основание перпендикуляра, опущенного из точки М на директрису. Очевидно y² = 2px. (4)

(4) – каноническое уравнение параболы.

Исследуем форму параболы по её уравнению.

Так как уравнение (4) содержит у только в четной степени, то парабола симметрична относительно оси Ох достаточно рассмотреть часть параболы, лежащую в верхней полуплоскости () :

– если х < 0, то уравнение дает мнимые значения у левее оси Оу ни одной точки параболы нет;

– если х = 0, то у = 0 начало координат лежит на параболе и является самой «левой» её точкой;

– при возрастании х возрастает у, причем если , то .

Таким образом, переменная точка , перемещающаяся по параболе, исходит из начала координат с ростом х и движется «вправо» и «вверх», причем при точка М бесконечно удаляется как от оси Оу, так и от оси Ох. Симметрично отражая рассмотренную часть параболы относительно оси Ох, получаем всю параболу.

Точка О пересечения параболы с осью абсцисс называется ее вершиной. Ось координат Ox является осью симметрии и называются ее осью параболы.

Геометрический смысл параметра р состоит в том, что он характеризует «ширину» области, ограниченной параболой: пусть и – симметричные относительно оси параболы точки. Расстояние тем больше, чем больше р.

Замечание. Если в системе координат ось ординат перпендикулярна директрисе d, а парабола расположена в верхней полуплоскости, то уравнение параболы x² = 2py можно записать в хорошо известном виде квадратичной функции . При этом директриса расположена в нижней полуплоскости системы координат и задается уравнением .

ПРЕОБРАЗОВАНИЕ КООРДИНАТ

Задача: Зная координаты точки в одной системе координат, найти её координаты в другой системе.

1. Параллельный перенос осей координат

Д

у

ана прямоугольная система координат Оху и точка в ней. Перенесем начало координат в точку , не изменяя направления осей. Получим новую систему координат О₁ХУ. Выразим Х, У через х, у. При любом расположении точек будем иметь: ОА + АР = ОР, где ОА = а, ОР = х, АР = Х. аналогично для У: