1. Свойства функции распределения

Свойство . Вероятность того, что случайная величина примет какое-либо значение , удовлетворяющее неравенству , равна приращению функции распределения на этом интервале:

.

­Доказательство. Разобьём событие на два несовместных события: и . Тогда получим (по теореме о сложении вероятностей несовместных событий):

.

Поскольку первые две вероятности, участвующие в последнем равенстве, суть функции распределения, постольку получается такое равенство:

,

откуда и получается:

.

Что и требовалось доказать.

Свойство . Функция распределения равна: от минус бесконечности - нулю, а от плюс бесконечности - единице. Иными словами:

.

­ Доказательство. Поскольку - есть вероятность пустого множества, постольку , а т.к. - есть вероятность достоверного события, то .

Что и требовалось доказать.

Свойство . Функция распределения (любой случайной величины) - неубывающая функция.

Доказательство. Поскольку (свойство )

при , а вероятность всегда

,

постольку

, т.е. при .

Что и требовалось доказать.

Таким образом, функция распределения не убывает, её значения расположены на отрезке . При стремлении функция распределения обращается в ноль, а при стремлении функция распределения обращается в единицу. Примерный график функции распределения приведён на рис 6.2:

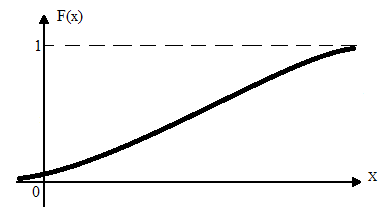
Рис. 6.2. Функция распределения непрерывной случайной величины.

Свойство . Если функция распределения непрерывна в точке , то вероятность того, что случайная величина принимает значение , равна нулю:

.

Доказательство. Оценим вероятность :

,

причём это верно для любого . Но по свойству

.

Теперь перейдём к пределу (т.к. - любое) в этом неравенстве (неравенство сохранится):

.

Предел слева равен самому выражению, а справа запишем выражения (обозначения) для пределов:

.

Поскольку предел справа равен (для непрерывной функции)

,

а предел слева также равен (для непрерывной функции)

,

постольку

.

Что и требовалось доказать.

Следствие (из свойства ). Для непрерывной функции распределения справедливо следующее:

.

Доказательство. Поскольку по свойству :

,

а отличается от только , т.е. вероятностью, которая равна (по свойству ), постольку:

.

Последнее равенство справедливо по теореме о сложении вероятностей несовместных событий. Аналогично доказываются два других равенства.

3. Плотность распределения вероятностей непрерывной случайной величины

Определение. Плотностью распределения вероятностей (или сокращённо плотностью вероятности) непрерывной случайной величины называется производная от её функции распределения , если только существует эта производная:

.

_______________

Пример. Найти плотность вероятности случайной величины (величины Релея), которая принимает неотрицательные значения, а её функция распределения равна .

Решение. Т.к. и не убывает ( при ), то на самом деле

.

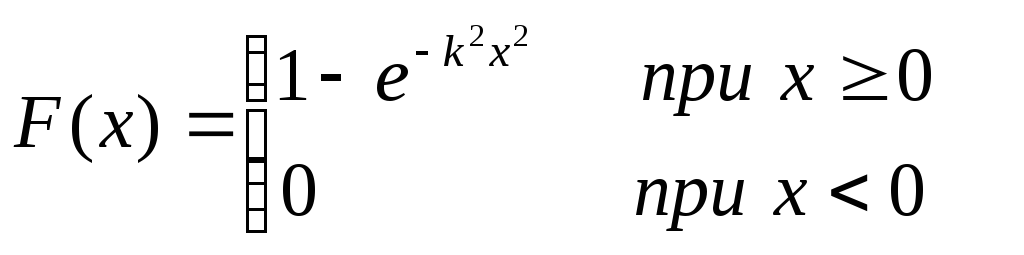Поэтому

.

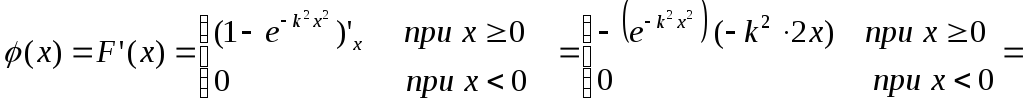
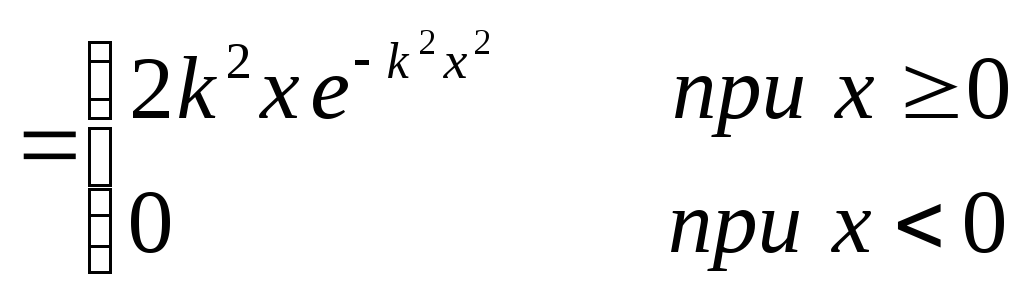Свойства плотности вероятности

Свойство . Вероятность того, что случайная величина примет какое-либо значение из замкнутого интервала , равна

.

Доказательство. Функция распределения - непрерывна, т.к. существует производная . Поэтому по следствию (из свойства ) для непрерывной функции распределения:

,

а по формуле Ньютона-Лейбница:

.

Поэтому .

Что и требовалось доказать.

Пример. Плотность вероятности случайной величины задана:

.

Найти вероятность того, что случайная величина примет значение на интервале .

Решение. По только что доказанному свойству

.

Свойство . Функция , плотность распределения вероятностей , всегда неотрицательна, т.е.

.

Доказательство. Поскольку при (по свойству для функции распределения), то:

,

как отношение двух неотрицательных величин).

Что и требовалось доказать.

Свойство . .

Доказательство. По только что установленному свойству () плотности вероятности:

при любом достаточно большом . Но по свойству для плотности вероятности:

при любом достаточно большом . Следовательно:

по следствию для непрерывной функции распределения. Откуда, переходя к пределу при (неравенство сохранится), получаем:

.

Откуда по свойству для функции распределения:

.

Поскольку вероятность события не может быть больше , постольку

.

Что и требовалось доказать.

В силу доказанных сейчас свойств, функция плотности распределения вероятностей всегда неотрицательна (по свойству ). Она стремится к нулю при стремлении и (т.к. по свойству площадь между графиком функции и осью абсцисс равна единице). Примерный график функции плотности распределения вероятностей изображён на следующем рис 6.3.

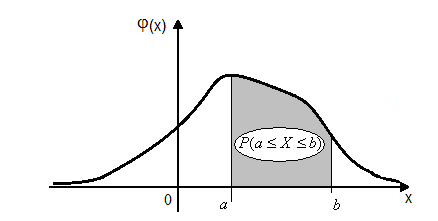
Рис. 6.3. Иллюстрация свойств 1-3 функции плотности распределения.

Свойство . Функция распределения равна

.

Доказательство. Для несобственного интеграла

Справедливо:

,

а по свойству для плотности распределения вероятностей:

.

По следствию из свойства для непрерывной функции распределения:

.

Поэтому, переходя к пределу, получим:

.

По свойству для функции распределения , т.е.

.

Что и требовалось доказать.

Итак, для полной характеристики случайной величины достаточно знать или функцию распределения, или плотность распределения вероятностей (т.к. одну из них можно выразить через другую):

или .

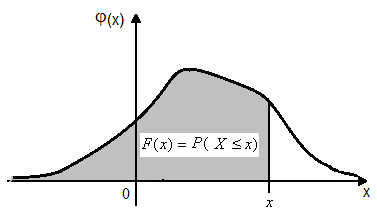
Рис. 6.4. Иллюстрация свойства 4 функции плотности распределения.

______________

Пример. Найти функцию распределения случайной величины, плотность вероятности которой:

.

Решение. По только что доказанному свойству:

.

Лекция № 7

Примеры распределения непрерывных случайных величин