9.3 Аналитический поиск экстремума целевой функции

Если целевая функция является аналитической и дифференцируема, то ее экстремальное значение может быть найдено методами дифференциального исчисления.

Если y = F(х), т. е. независимая переменная одна, то рассматриваются первая производная функции F(х)

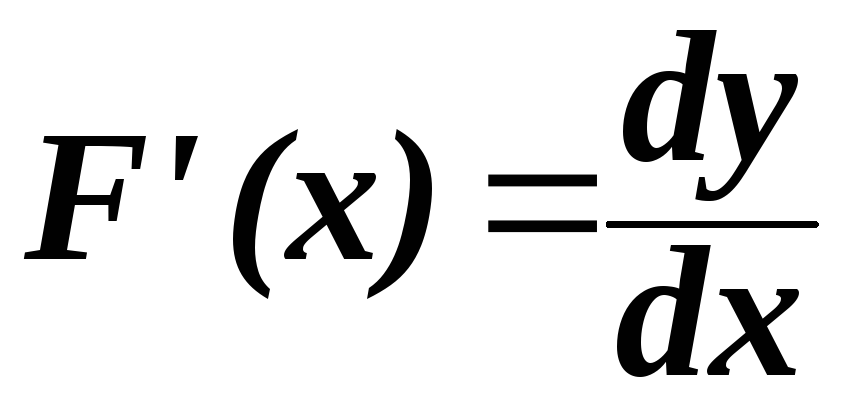
и вторая производная

.

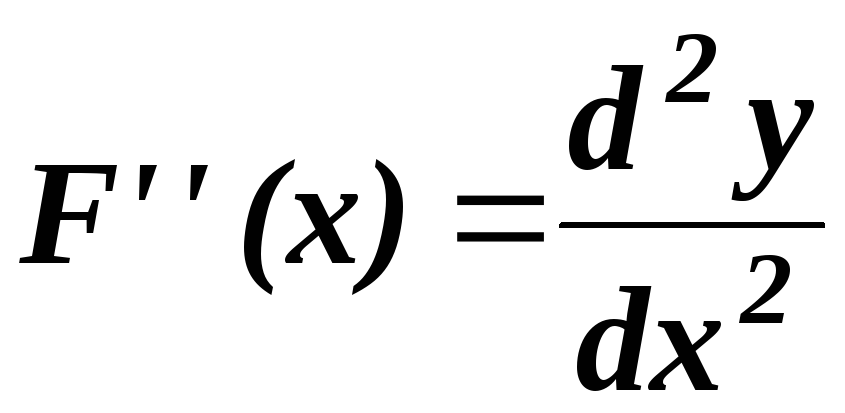Экстремум находят, приравнивая первую производную нулю и определяя знак второй производной. При этом, если , то имеется минимум, если , то имеется максимум целевой функции.

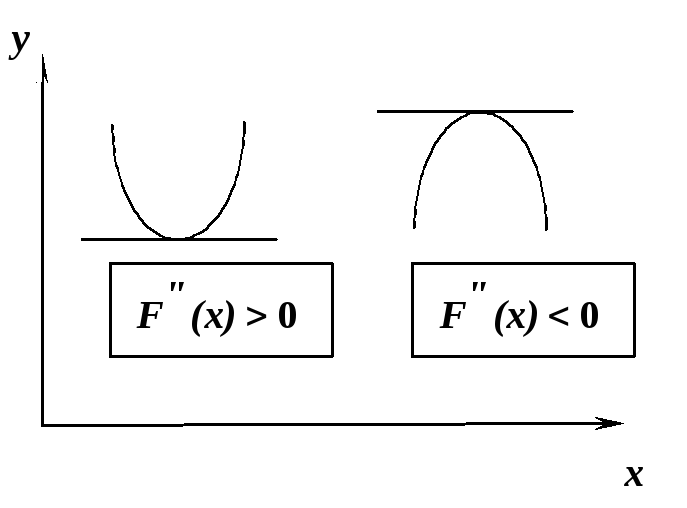
Рис. 9.2

Если F(x) = 0, то нужно провести дополнительный анализ. Обычно берут высшие производные и, если они не равны 0, то нет ни максимума, ни минимума.

В качестве примера можно рассмотреть кубическую параболу:

что не равно 0.

Следовательно, у кубической параболы нет ни максимума, ни минимума.

Если переменных несколько, т.е. , то рассматриваются частные производные: .

Классический метод поиска экстремума заключается в решении системы нормальных уравнений:

Типичная задача – расчет коэффициентов регрессионной модели методом наименьших квадратов. В ней критерий оптимальности – сумма квадратов отклонений, а оптимизирующие факторы – значения рассчитываемых коэффициентов регрессии.

Чтобы убедится в том, что полученные в результате решения системы уравнений значения факторов оптимальны, т.е. их совокупность определяет оптимальное решение задачи, необходимо выяснить следующие обстоятельства:

• действительно ли решение определяет экстремум (а не седловую точку или точку перегиба);

• получается ли экстремум того знака (максимум или минимум), который нас интересует;

• если система имеет несколько решений, то какое из них отвечает глобальному оптимуму, а какое – локальным; глобальным будет тот, который выше или ниже всех остальных, а остальные – локальные.

• все ли ограничения соблюдаются в точке оптимума.

9.4 Численные методы поиска оптимума

Численные методы применяют в случаях, когда:

• в точке экстремума отсутствуют производные целевой функции;

• целевая функция задана таким образом, что продифференцировать ее в общем виде не удается;

• для решения системы уравнений нужны настолько громоздкие вычисления, что численные методы оказываются проще и их применение эффективнее.

9.4.1 Оптимизация перебором

Если число возможных вариантов значений факторов целевой функции конечно, достаточно рассчитать целевую функцию для всех этих вариантов и выбрать её максимальное (или минимальное) значение.

Например, можно рассчитать параметр оптимизации для случаев протекания процессов в аппаратах всех стандартных размеров и выбрать лучший вариант.

Перебор целесообразно осуществлять на ЭВМ. При этом все варианты могут быть записаны в памяти машины, что имеет место при создании систем автоматического проектирования – САПР. Применение перебора иногда позволяет найти и такие варианты, до которых без ЭВМ дойти практически было бы невозможно.

9.4.2 Сканирование

Метод сканирования близок к методу перебора, но применяется к непрерывным функциям.

Рассмотрим поиск максимума или минимума функции от одного фактора при пределах его изменения в интервале от a до b, где a и b – ограничения.

Интервал [a, b], на котором требуется отыскать экстремум целевой функции, – это интервал неопределенности. Необходимо сузить этот интервал в области оптимума.

Выбирают целое число q значений целевой функции, которое придется рассчитывать. Определяют ширину частного интервала 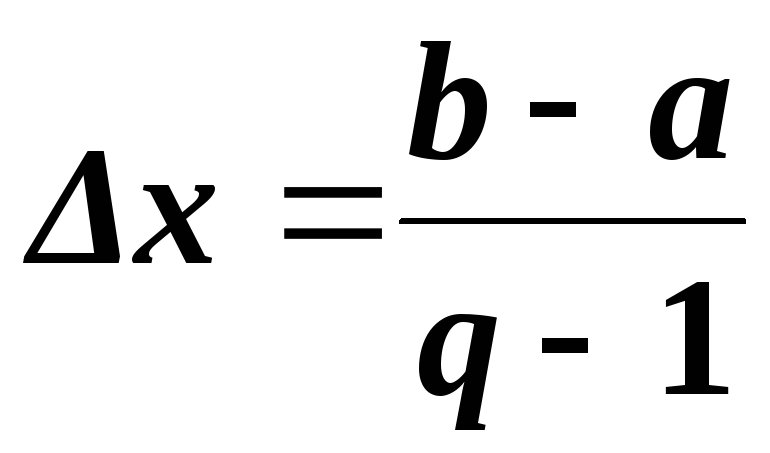. Концы каждого частного интервала на отрезке [a, b] называются узлами. В каждом узле рассчитывают значение F(x). За максимум выбирают наибольшее значение, за минимум – наименьшее значение. 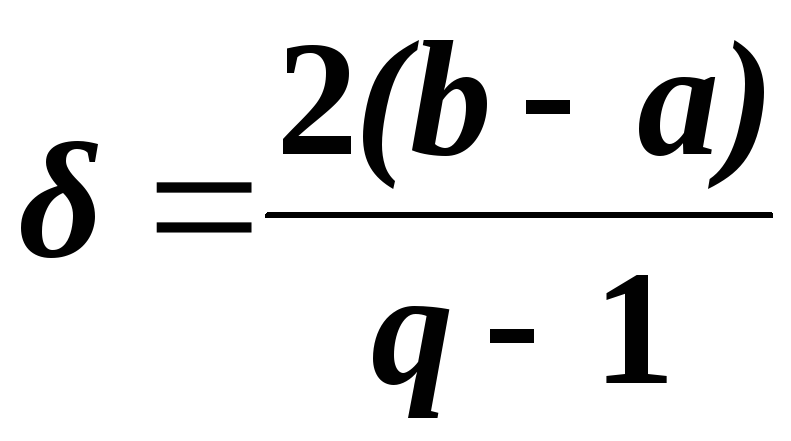Истинный экстремум может находиться либо справа, либо слева от наилучшего значения и таким образом интервал неопределенности, равный , содержит оптимальное значение функции y = F(х).