2. Нечёткие предикаты

«Чёткие» предикаты определяются как функции на множестве «термов» , принимающие значения в булевом пространстве . Так, если , то примером одноместного предиката , где , может служить функция

. (4)

Аналогично определяются двухместные, трехместные и т.п. предикаты. Например, двухместный предикат определен на множестве .

Нечёткий предикат мы определяем как функцию, заданную на множестве и принимающую значения в пространстве векторных нечетких переменных , которое было определено выше. Используя полужирный шрифт в обозначении предиката , мы подчеркиваем тот факт, что областью значений предиката являются нечеткие логические векторы, или , причем для всех

(5)

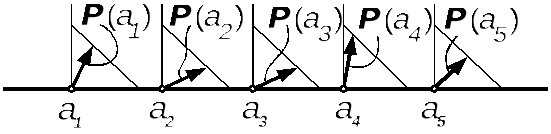
Таким образом, нечёткий предикат задает на некоторое векторное поле, как это показано на рис. 1.

Рис. 1. Пример нечёткого предиката как векторного поля нечётких переменных, заданного на множестве

Так как предикаты являются логическими переменными, то к ним могут быть применены все нечёткие логические операции, введенные в [2] и кратко рассмотренные выше. Это позволяет из некоторых заданных на предикатов строить новые, более сложные, предикаты, дает возможность расширить на область предикатов правила логического вывода.

Правило «модус поненс» можно проиллюстрировать следующим простым примером. Пусть между предикатами , заданными на , существует связь (в приложениях связи такого рода называют «правилами»)

. (7)

Здесь предикат можно интерпретировать как степень истинности того, что «из следует ». Перепишем (7) в матричном виде

или . (8)

Это соотношение можно использовать двумя способами. 1) Пусть нам известны предикаты , и пусть определитель матрицы не равен нулю, то есть . В этом случае решение уравнения (8) позволяет найти предикат в виде . 2) Будем считать, что нечёткие предикаты и , заданны на множествах и соответственно () и что вместо (8) имеет место более общее правило

. (9)

Как и в первом случае, мы должны вычислить из равенства (9) , однако предикат задан не напрямую, а заданы некоторые дополнительные правила вида

, (10)

справедливые для множества вариантов, нумеруемых индексом , и для каждого из вариантов известны предикаты и .

При решении конкретных задач предсказать значения предикатов и бывает легче, чем прогнозировать общий результат импликации (9) . По формуле (10) мы можем найти частные результаты, имеющие место при выполнении отдельных вариантов . Предполагая, далее, что в общем результате присутствуют все варианты, для вычисления и используем формулы

(11)

Поскольку в нечёткой логике законы дистрибутивности не выполняются, мы не можем получить из соотношений (10) и (11) связь между предикатами . Поэтому используем выражение (9), которое служит дополнительным правилом вывода. Обращая формулу (9), получаем

. (12)

Метод резолюций для логики нечетких предикатов также может быть расширен по сравнению с тем, как это сделано для логики нечётких высказываний в [2]. Из-за недостатка места мы опустим здесь изложение этого метода.