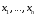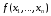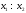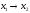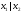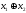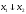Лекция 2-3 Алгебра высказываний. Логические функции. Законы булевой алгебры

Алгебра логики — раздел математической логики, изучающий строение сложных логических выска­зываний и способы установления их истинности с помощью алгебраических методов.

Чтобы понять сущность алгебраического под­хода к логике, вспомним обычную школьную алгебру, которую можно назвать алгеброй арифме­тики. Основные ее объекты — формулы, состоящие из букв, знаков арифметических операций и ско­бок. Буквы обозначают переменные, которые мо­гут принимать числовые значения. С формулами производят процедуры двух видов: вычисления и преобразования. Вычисление формулы заключает­ся в том, что вместо букв подставляются числа; знаки указывают действия, а скобки — в каком по­рядке эти действия с подставленными числами на­до выполнить. Каждая формула задает некоторую арифметическую функцию; число аргументов (пе­ременных) этой функции равно числу различных букв в формуле. Множество различных формул и задаваемых ими функций бесконечно; однако все они строятся с помощью небольшого числа элемен­тарных функций, называемых арифметическими операциями — сложения, умножения и т. д. Пре­образование формулы заключается в том, что ис­ходная формула F₁ или ее часть заменяется другой формулой, в результате чего получается новая формула F₂, которая эквивалентна F₁ в следую­щем смысле: формулы F₁ и F₂ задают одну и ту же функцию, т. е. при любых значениях переменных вычисления F₁ и F₂ дают один и тот же результат. Преобразования формул производятся на основа­нии законов арифметики (ассоциативного, коммукативного и дистрибутивного законов, равенства а - а = 0 и др.), а также полученных из них соот­ношений типа (а + b)² = а² + 2ab + b² и т. д.

По аналогичным принципам строится и алгебра логики. Разница заключается в следующем. В фор­мулах алгебры логики переменные являются логи­ческими или двоичными, т. е. принимающими только два значения — "ложь" и "истина", которые обозначаются либо 0 и 1, либо Л и И, либо false и true. Знаки операций обозначают логические опе­рации (логические связки). Каждая формула задает логическую функцию: функцию от логических пе­ременных, которая сама может принимать только два логических значения. Любую логическую фун­кцию 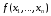можно задать таблицей, в левой части которой выписаны все возможные наборы значений ее аргументов 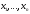, а правая часть представляет собой столбец значений функции, со­ответствующих этим наборам:

набор значений аргументов	значение (0 или 1) функции

Число строк в такой таблице равно 2ⁿ — числу возможных наборов значений аргументов, т. е. чис­лу различных комбинаций длины п из нулей и еди­ниц. Число различных функций п переменных равно 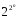— числу возможных расстановок нулей и единиц в столбце с 2ⁿ строками.

Таблица функции f(x) одной переменной со­держит всего две строки, а самих функций одной переменной — четыре :

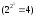x f(x) 0 1 0 0 x	f(x)
0 1	0 1

f(x)=x

(повторение)

константа 0

x	f(x)
0 1	0 0

x	f(x)
0 1	0 0

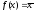
(отрицание)

константа 1

Таблица функции 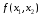двух переменных содержит четыре строки, а самих функций двух переменных — шестнадцать (). Укажем наиболее важные из них. Пять функций соответст­вуют логическим связкам (см. перечень связок и обозначений для них в статье "Математическая логика"):

Таблица 1

Таблица 2

x1	x2	x1& x2
0	0	0
0	1	0
1	0	0
1	1	1

x1	x2	x1V x2
0	0	0
0	1	1
1	0	1
1	1	1

Дизъюнкция

(ИЛИ)

Конъюнкция

(И)

x1	x2
0	0	1
0	1	0
1	0	0
1	1	1

x1	x2
0	0	1
0	1	1
1	0	0
1	1	1

Импликация

Таблица 3

Таблица 4

Эквивалентность

Импликация

Кроме того, часто употребляются ещё две функции двух переменных:

Таблица 5

Таблица 6

x1	x2
0	0	1
0	1	1
1	0	1
1	1	0

x1	x2
0	0	0
0	1	1
1	0	1
1	1	0

Штрих Шеффера

(НЕ-И)

Неравнозначность

(сложение по модулю два)

Таблица 7

x1	x2
0	0	1
0	1	0
1	0	0
1	1	0

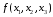Значение любой логической формулы, содер­жащей знаки этих функций, на значений переменных можно вычислить, используя эти таблицы. Пусть, например, функция трех переменных задана формулой

Стрелка Пирса

(НЕ-ИЛИ)

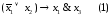
Стрелка Пирса

Вычислим эту функцию на наборе 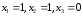. (Логически это значит: определим значение истинности сложного высказывания (1) при усло­вии, что составляющие его простые высказывания х₁ и х₂ истинны, а х₃ — ложно.) Подстановка значений в формулу (1) дает

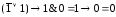
Вычислив эту формулу на остальных 7 наборах значений х₁, х₂, х₃, полностью восстановим табли­цу этой функции.

Таблица 8

x1	x2	x3
0	0	0	0
0	0	1	0
0	1	0	0
0	1	1	0
1	0	0	1
1	0	1	1
1	1	0	0
1	1	1	1

Таким образом, от функции, заданной в виде формулы (выражения), всегда можно перейти к табличному заданию. Ответ на обратный вопрос:

всегда ли от таблицы функции можно перейти к формуле — не столь однозначен и зависит от того, какие операции предполагается использовать в формулах. Формула, задающая функцию, факти­чески определяет ее через набор других функций, которые выбраны в качестве исходных и обозначены знаками операций. (В формуле (1) операциями являются конъюнкция, дизъюнкция, отрицание и импликация.)

Существуют наборы логических функций, с по­мощью которых можно выразить любые другие ло­гические функции. Такие наборы называются функционально полными наборами или базисами. Наиболее известный и изученный базис — набор "И", "ИЛИ", "НЕ" (конъюнкция, дизъюнкция, от­рицание). Множество всех логических функций, на котором определены эти три операции, называется булевой алгеброй; операции и формулы булевой ал­гебры также часто называют булевыми.

Функциональная полнота булевой алгебры оз­начает, что переход от табличного задания к буле­вой формуле всегда возможен. Метод перехода заключается в следующем: для каждого набора зна­чений переменных 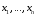на котором функция 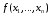равна 1, выписывается конъюнкция всех переменных; над теми переменными, которые в этом наборе равны 0, ставятся отрицания; все та­кие конъюнкции соединяются знаками дизъюнк­ции. Полученная формула называется совершенной дизъюнктивной нормальной формой (СДНФ) логи­ческой функции . 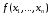СДНФ для каждой функции единственна, как говорят в математике, с точностью до перестановок переменных или конъ­юнкций. Это означает, что две различные СДНФ одной функции могут отличаться только порядком конъюнкций и расстановкой переменных в конъюн­кциях. Для функции, заданной табл. 8, СДНФ име­ет вид:

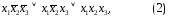
а для импликации (см. табл. 3)

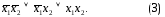
(При написании формул булевой алгебры с конъ­юнкцией принято обращаться так же, как в обыч­ной алгебре — с умножением: знак конъюнкции и скобки, ее окружающие, опускаются.)

СДНФ обычно весьма громоздкая формула. Упрощение формул в булевой алгебре (как и в лю­бой другой алгебре) производится на основе

экви­валентных преобразований, опирающихся на основные законы (эквивалентные соотношения), которые в каждой алгебре — свои.

В булевой алгебре эти законы — следующие.

1. Ассоциативность дизъюнкции и конъюнк­ции:

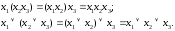
2. Коммутативность дизъюнкции и конъюнк­ции:

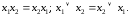
3. Дистрибутивность конъюнкции относитель­но дизъюнкции:

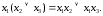
4. Дистрибутивность дизъюнкции относитель­но конъюнкции:

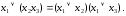
5. Идемпотентность (отсутствие степеней и ко­эффициентов) :

6. Закон двойного отрицания:

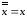
7. Свойства констант 0 и 1:

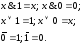
8. Правила де Моргана:

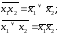
9. Закон противоречия:.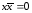

10. Закон исключенного третьего:

Законы 1, 2, 3, 7 показывают, что свойства конъюнкции очень похожи на свойства умножения; поэтому ее часто называют логическим умножени­ем. Из законов 6 и 8 следует, что, используя отри­цание, дизъюнкцию можно выразить через конъюнкцию, и наоборот:

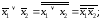
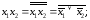
Это означает, что наборы {И, НЕ} и {ИЛИ, НЕ} также являются функционально полными.

Эквивалентные соотношения, т. е. две форму­лы, соединенные знаком равенства, — это утверж­дения о том, что данные формулы выражают одну и ту же функцию, т. е. при любых значениях, вхо­дящих в них переменных принимают равные зна­чения. Поскольку число различных наборов значений логических переменных конечно, эквива­лентные соотношения алгебры логики можно дока­зывать, перебрав все эти наборы (т. е. по существу построить таблицы функций для левой и правой формул и убедиться, что они совпадают). Такой способ доказательства громоздок; однако без него нельзя обойтись только при доказательстве основ­ных законов (1 — 10). Другие соотношения, часто применяемые в преобразованиях булевых формул, проще выводить с помощью основных законов. При­ведем три наиболее распространенных соотноше­ния:

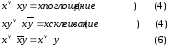
Например, соотношение (4) выводится из ос­новных законов следующим образом (последова­тельно используются законы 7, 3, 7, 7):

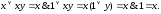
В свою очередь, используя основные законы и соотношения (4) — (6), можно заметно упростить формулы (2) и (З):

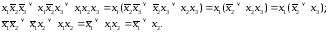
Последняя формула является наиболее про­стым представлением импликации в булевой алгеб­ре:

Другие функции двух переменных представля­ются в булевой алгебре следующими формулами:

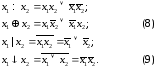
Заменив в формуле (1) импликацию ее буле­вым представлением, получим формулу, которая легко преобразуется в формулу (7)

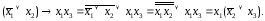
Наряду с булевым базисом хорошо изучен ба­зис Жегалкина, состоящий из конъюнкции, сложе­ния по модулю 2 и константы 1. Переход к булеву базису осуществляется по формулам

Базис может состоять из одной функции: при­мерами являются стрелка Пирса и штрих Шеффера. Для того чтобы доказать функциональную полноту набора функций, достаточно показать, что через них можно выразить дизъюнкцию (или конъюнк­цию) и отрицание. Покажем это для штриха Шеф­фера. Из формул (9) следует, что

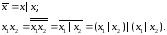
Алгебра логики лежит в основе анализа и про­ектирования логических схем. Логические схемы состоят из логических элементов, осуществляющих логические операции. Набор операций, осуществ­ляемых элементами, должен быть функционально полным. Анализ логической схемы, т. е. выяснение того, какие двоичные (логические) сигналы появят­ся на выходах этой схемы после подачи определен­ных входных двоичных сигналов, сводится в конечном счете к серии логических вычислений. Проектирование и оптимизация логических схем, т. е. построение схем, реализующих заданные пре­образования с как можно меньшим числом элемен­тов, проводится с использованием эквивалентных преобразований в различных логических базисах.

Любая сколько-нибудь сложная программа для ЭВМ содержит условные переходы и связанные с ними логические условия, установление истинно­сти которых требует вычисления логических выра­жений по правилам алгебры логики. Поэтому логические операции имеются практически во всех универсальных языках программирования. При этом логические значения обычно имеют отличные от 0 и 1 обозначения (например, true и false), чтобы не путать их с арифметическими.