
Обчислення одномірних моментних функцій по характеристичним
Розглянемо одномірну характеристичну функцію
![]()
та обчислимо по аргументу vk першу похідну від неї:
![]()
Для vk = 0 маємо:

Початкове значення (для vk = 0) похідної 1-го порядку одномірної характеристичної функції з точністю до постійного множника j визначає математичне очікування або одномірну початкову функцію 1-го порядку:
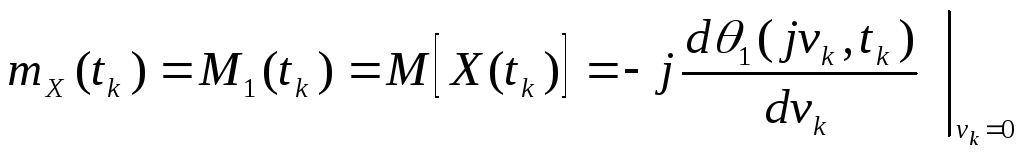
Друга похідна одномірної характеристичної функції

Тоді середній квадрат

Одномірна моментна функція 2-го з точністю до (-j)2 пропорційна другій похідній від одномірної характеристичної функції в точці vk = 0.
Приклад.
Розглянемо процес X(t) з експоненціальним законом розподілу

Математичне
очікування такого процесу в перерізі
![]() :
:
![]()
Середній квадрат:

Тоді дисперсія може бути обчислена як різниця між середнім квадратом та квадрати середнього значення:
![]()
Обчислимо ці ж величини на основі характеристичної функції 1-го порядку

Перша похідна характеристичної функції:
![]()
Початкове значення похідної:
![]()
Тоді
![]()
Початкове значення другої похідної

Отже,
середній квадрат
![]()
Результати розрахунків з використанням характеристичних функцій повністю співпадають з отриманими раніше на базі визначень математичною очікування та середнього квадрату.
Характеристична функція закону Лапласа

Оскільки
![]() парна, то
парна, то
![]() .
.
За методом характеристичних функцій:
![]()
Дисперсія тоді є середньостатистичним квадратом:

Експоненціальний закон та його узагальнення часто використовується для вирішення технічних проблем, пов'язаних з визначенням надійності систем, часу очікування доступу користувачів в яку-небудь систему (канали телефонного, телеграфного зв'язку чи, наприклад, мережа Internet), числа каналів системи зв'язку, необхідних ,для реагування на повідомлення користувачів, що поступають у випадкові моменти часу та характеризуються довільною довжиною.
Приклад.
Гармонічне
коливання характеризується випадковою
початковою фазою
![]() з рівномірним законом розподілу
з рівномірним законом розподілу
![]() на інтервалі
на інтервалі
![]() і детермінованими амплітудою та частотою:
і детермінованими амплітудою та частотою:
![]()
Визначити середнє статистичне, середній квадрат та дисперсію початкової фази.
У
зв'яжу з тим, що функція щільності
ймовірності симетрична відносно осі
ординат, математичне очікування
![]() .
.
Середнє значення квадрату початкової фази процесу з таким законом розподілу ймовірностей згідно з отриманим раніше результатом
![]()
Значення
середнього квадрату визначає дисперсію
![]() ,
оскільки математичне очікування дорівнює
нулю.
,
оскільки математичне очікування дорівнює
нулю.
Тепер обчислимо ці ж характеристики на основі одномірної характеристичної функції:

Середній квадрат випадкової початкової фази
![]()
Після двократного диференціювання та розкриття невизначеності отримаємо середній квадрат га дисперсію:

Отже, знаючи одномірну характеристичну функцію на основі ( ) і ( ), ми можемо обчислювати одномірні моментні функції відповідних порядків, навіть, більше другого.
Приклад.
Випадковий
прогрес X(t)
в k-ому
перерізі визначається дискретною
випадковою величиною
![]() ,
ймовірності прийняття значень якого
задаються рядом
,
ймовірності прийняття значень якого
задаються рядом
![]() .
Визначити середній квадрат та математичне
очікування процесу в заданому перерізі
методом характеристичних функцій.
.
Визначити середній квадрат та математичне
очікування процесу в заданому перерізі
методом характеристичних функцій.
Згідно з означенням для дискретної випадкової величини одномірна характеристична функція
![]()
Перша похідна характеристичної функції по її аргументу:
![]()
а її початкове значення
![]()
Тоді відповідно до ( ) математичне очікування
![]()
Для визначення середнього квадрату обчислимо початкове значення другої похідної характеристичної функції:

Згідно з ( ) середній квадрат
![]() .
.
Поибки 6 лекція
Приклад. Оцінити сумарну адитивну похибку ІВС, якщо Δадав = ±0,08; ΔБО=±0,02; параметри АЦП, як у попередньому прикладі: 2,0/0,5; нормуюче значення YН=1; КБО = 0,5; КАЦП =1
Знаходимо коефіцієнти впливу
![]()
Тоді
![]()
(![]() )
)
Тоді
![]()
Після того, як визначені адитивна та мультиплікативна складові для всієї системи їх об’єднують
ΔІВС = ΔY = ΔYа + ΔYм
δY
= δYм
+ δYa
= δYм
+
![]() =
δYм
+
=
δYм
+
![]()
Приклад:
![]()
Якщо величини ΔKi, Δаді є випадковими, то сумарна систематична похибка ІВС оцінюється математичним очікуванням співвідношень (4) з урахуванням коефіцієнтів впливу. Наприклад:
ΔІВСсист = М[ΔYa]+M[ΔYm]
Приклад
В.
Середньоквадратичні значення випадкової
похибки блоків такі:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Похибки корельовано, тоді
.
Похибки корельовано, тоді
![]()
Приклад С. Випадкова похибка ВК зміщується в межах ±2,5% і розподілена за рівномірним законом, а похибка блоку обробки підпорядкована нормальному закону розподілу і дорівнює ±0,05%. Похибки некорельовані визначити результуючу похибку системи.
Якщо
закон рівномірний в межах b,a,
то
![]() ,
а середньоквадратичне значення
,
а середньоквадратичне значення
![]() .
Отже, для довірчої ймовірності 1 =>
b-a=Δд(РД=1).
Тоді
.
Отже, для довірчої ймовірності 1 =>
b-a=Δд(РД=1).
Тоді
![]() .
У нашому випадку
.
У нашому випадку
![]() .
Таким чином,
.
Таким чином,
![]()
Для блоку обробки (норм. закон)
![]()
Остаточно,
![]()
Клас точності приладу – зведена похибка у відсотках:
