Лекція 1. Предмет, мета та завдання дисципліни

Приклад.

Послідовний електричний коливальний контур збуджується гармонічним сигналом . Реакція контура на таке збудження є розв'язком диференційного рівняння:

Тоді,

D_x - електрична напруга гармонічної форми амплітуди Х_m частоти та початкової фази ;

D_y - електрична напруга на ємнісному елементі в усталеному режимі роботи контура, теж гармонічна з параметрами U_mc , та ;

F - оператор диференціювання, додавання, множення.

Приклад.

Інтегруюча система, властивості якої визначаються імпульсною характеристикою , збуджується прямокутним відеоімпульсом. Реакція системи на таке збудження обчислюється за інтегралом Дюамеля або згортки:

Отже, в данному випадку: F - операція згортки; D_x - неперервний відеоімпульс; D_y -неперервний сигнал довільної форми.

Приклад.

Деяка система перетворює одномірний аналоговий сигнал за слідуючим законом:

Тоді, системний оператор:

Цьому виразу можна поставити у відповідність структурну схему, що утворена каскадним з’єднанням ідеального підсилювача і диференціатора.

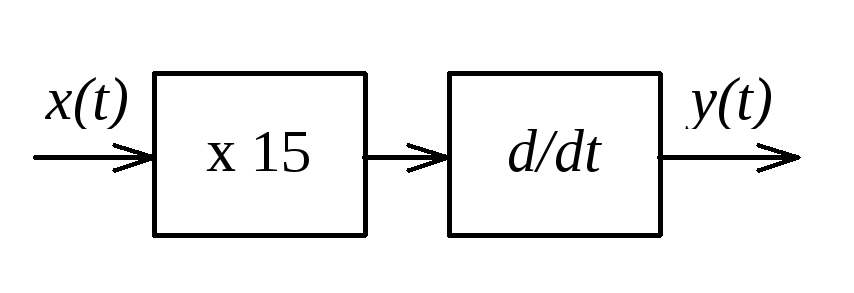
Рисунок 1.4 - Функціональна схема лінійної системи.

Лекція 3. Класифікація інформаційно-вимірювальних систем

 Приклад.

Математична модель деякої системи має такий вигляд: .

Тоді для діючого процесу маємо:

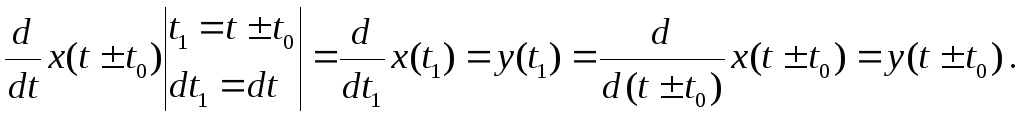
Умова стаціонарності (1.8) справджується, тому така система є стаціонарною з незалежним від операторм . Отже, для стаціонарної системи оператор F не є функцією часу, хоча може містити операції інтегрування та диференціювання відносно часової змінної.

◙

 Приклад.

Математична модель системи: . На дію реакція

Для інваріантної системи потрібно, щоб .

Отже, система є нестаціонарною. Це підтверджується залежністю від часової змінної t оператора системи .

 Приклад.

Деяка система (рис. 3.1) здійснює оброблення вхідного сигналу за законом . Визначити, чи є така система лінійною.

Якщо то згідно з принципом суперпозиції

Отже, система лінійна, а диференціювання, додавання, множення на сталу величину є лінійними операціями.

 Приклад.

Припустімо, що діючий процес є гармонічним сигналом виду . Реакція лінійної стаціонарної системи з оператором

є також гармонічною тієї самої частоти , але з іншою амплітудою .

 Приклад.

Певна система визначається співвідношенням: .

Раніше було встановлено, що вона належить до нестаціонарних систем. Водночас така система є лінійною, оскільки для неї виконується принцип суперпозиції:

.

 Приклад.

Розглянемо параметричну систему з таким системним оператором

.

Реакція на зазначену раніше гармонічну дію

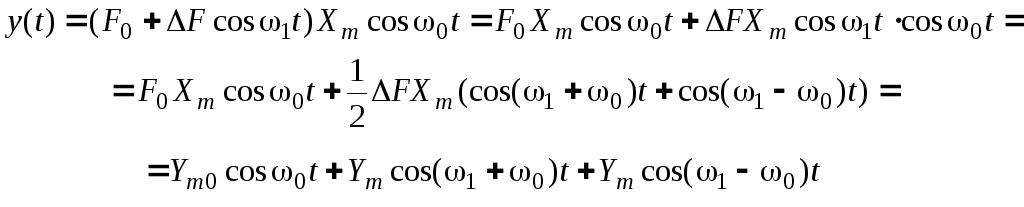
містить нові гармонічні складові з частотами і . Подібні зміни сигналів називають перетворенням частоти, що зумовлено появою в реакції складової з проміжною частотою .

 Приклад.

Реакція та дія ідеального квадратора задовольняють такому співвідношенню:

Дія на його вході суми сигналів на виході спричинює реакцію

замість відповідно до принципу суперпозиції. Наявність складової засвідчує, що ця система є нелінійною.

 Приклад.

Реакція на гармонічну дію нелінійної системи з оператором дорівнює

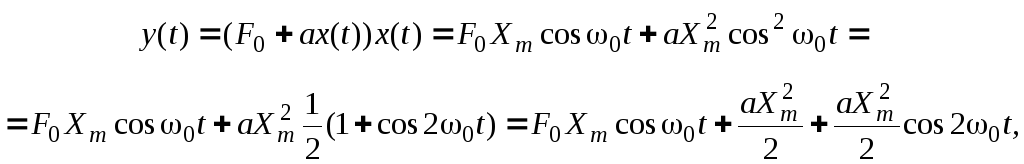
і містить постійну та дві гармонічні складові з частотами ω₀ та 2ω₀. Спектральних складових із подвоєною частотою у діючому сигналі немає, що є підтвердженням перетворення спектра.

 Приклад.

Максимальна робоча частота для каналів телефонного зв’язку . Довжина хвилі, яка відповідає цій частоті . Тоді очевидно, що такі елементи каналу як підсилювачі, мікрофони, фільтри тощо слід розглядати як системи із зосередженими параметрами. В той же час кабельні мережі каналу, довжина яких може перевищувати 100 км, слід вважати системами із розподіленими параметрами.

 Приклад.

Отримати різницеве рівняння, що відповідає лінійному диференціальному рівнянню з постійними коефіцієнтами

яке описує властивості лінійної динамічної системи (кола) першого порядку.

Відповідно до диференціального рівняння та (3.1) маємо

Прості перетворення дають шукане різницеве рівняння

яке і є математичною моделлю дискретної (цифрової) лінійної інваріантної в часі системи.

Реакція такої системи в будь-який дискретний момент часу є розв’язком різницевого рівняння:

 Приклад.

Визначити відлікові значення реакції лінійної нестаціонарної дискретної системи, різницеве рівняння якої на дію дискретного сигналу ?

Відповідно рівняння заданого рівняння відлікові значення реакції

Реакція заданої системи є дійсною.

Приклад.

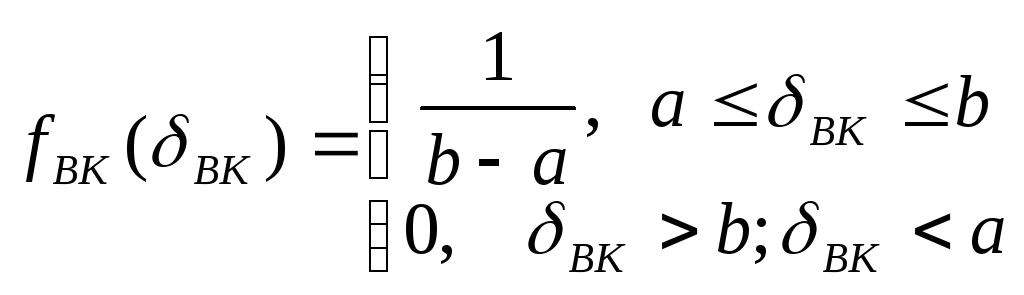
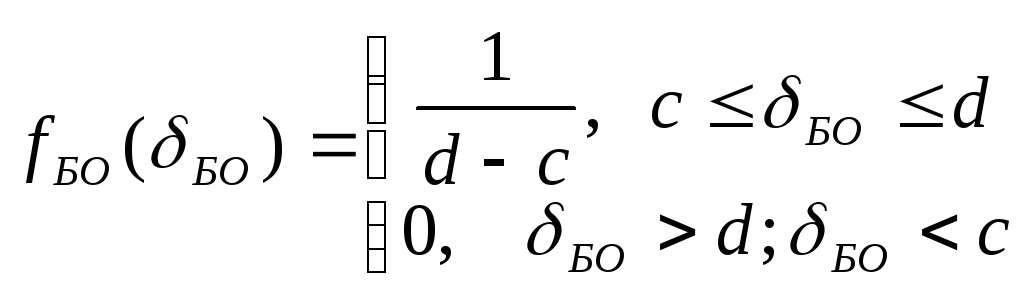
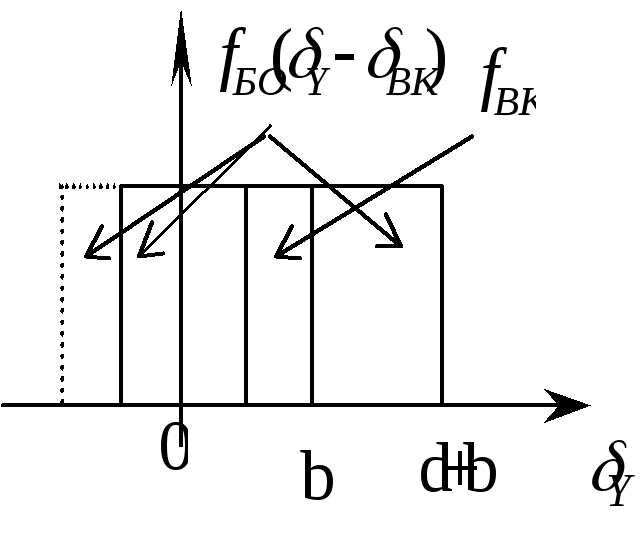
Як і перший, так і другий є рівномірними законами розподілу. Тоді, згідно з (3):

Для визначеності припустимо, що a = c = 0, b = d > 0.

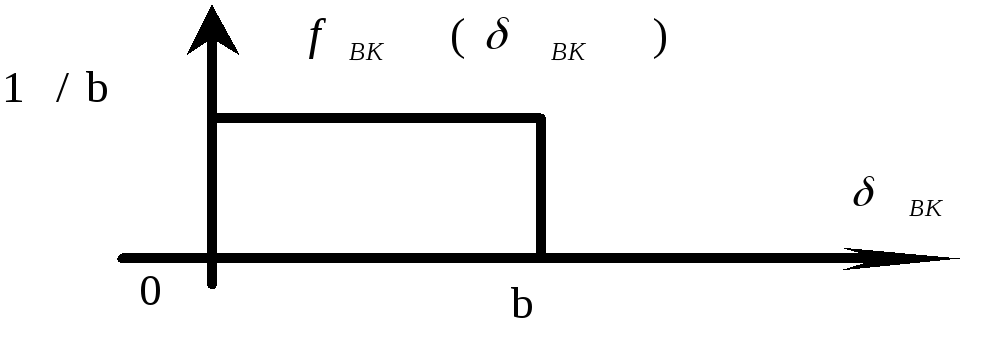
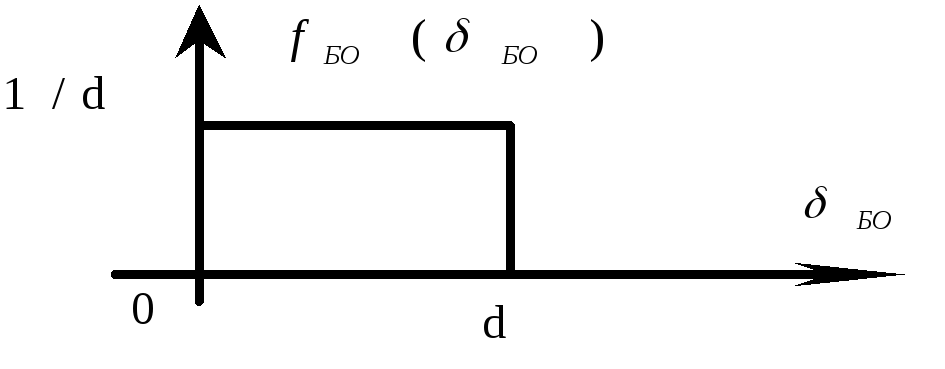
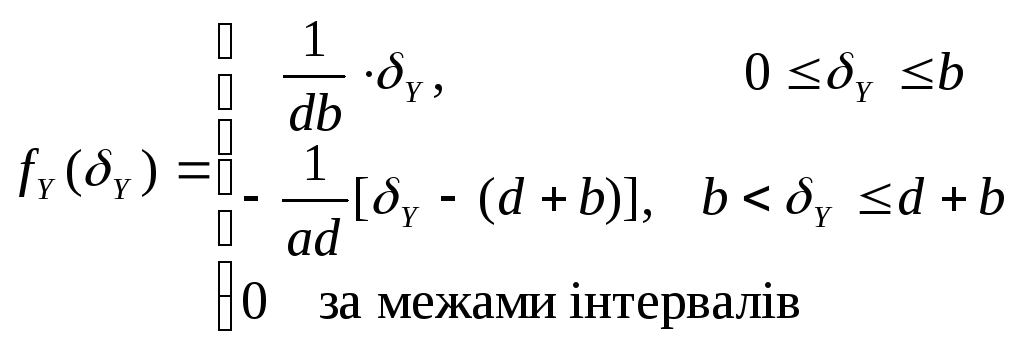
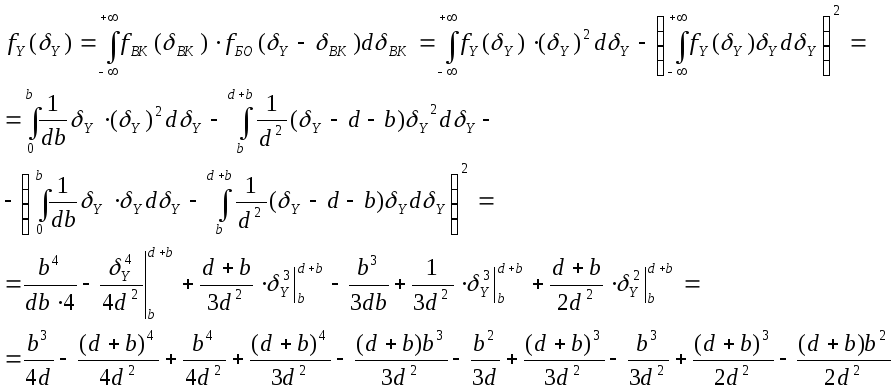
Приклад. Визначити закон розподілу ймовірностей повної похибки ІВС, якщо похибка ВК та БО підпорядкована закону розподілу Лапласа:

, , .

За основу беремо формулу (3), тобто інтеграл згортки.

Виходячи з парності і , розглянемо тільки випадок, коли . Визначення меж інтегрування при цьому ілюструється на рисунку.

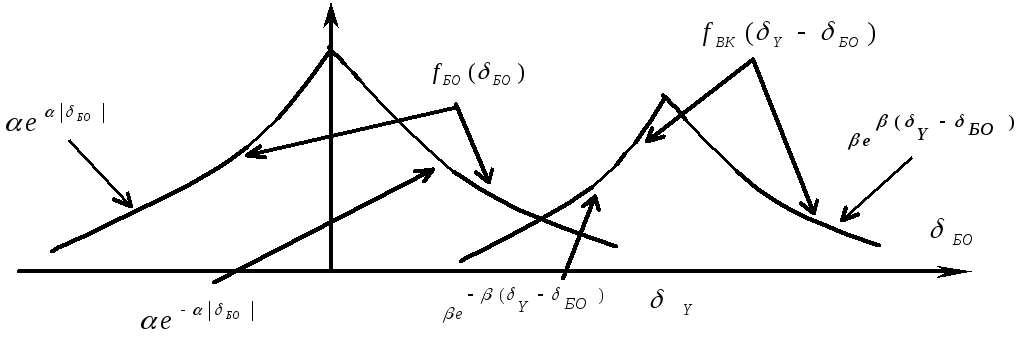
Рисунок – до визначення меж інтегрування.

Будемо пам’ятати, що функція є дзеркальним відносно вертикальної лінії в точці відображенням функції .

Отже, шукана кореляційна функція

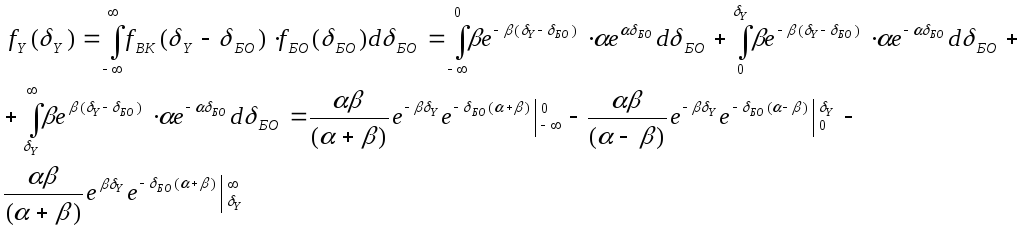
Для підстановки меж інтегрування та спрощень отримаємо:

Можна очікувати, що за парності законів розподілу результат буде парний.

Слід звернути увагу на те, що якщо в приведеній вище формулі спрямувати до , то

що відповідає кореляційній функції реакції інтегруючого кола з тією ж імпульсною характеристикою при дії на нього білого шуму.

Обчислення законів розподілу ймовірностей повної похибки методом інтеграла згортки є достатньо непростою проблемою, особливо, що стосується вибору меж інтегрування для різних законів розподілу ймовірностей похибок окремих блоків ІВС.

Одним із способів вирішення проблеми є застосування методу характеристичних функцій.

Приклад.

Обчислити характеристичну функцію, що відповідає закону розподілу Лапласа

Тоді обернене перетворення

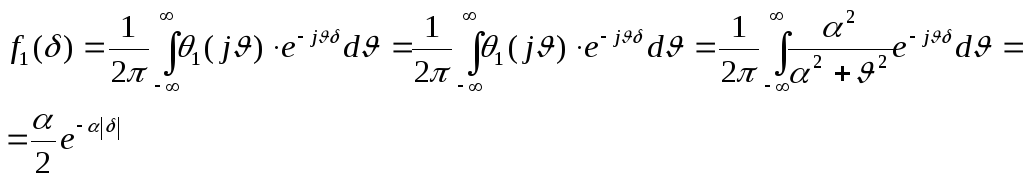
Приклад.

Обчислити функцію щільності ймовірностей, а також характеристичну функцію випадкового процесу, інтегральний закон розподілу ймовірності якого:

Функція щільності ймовірності

Тоді характеристична функція 1 -го порядку

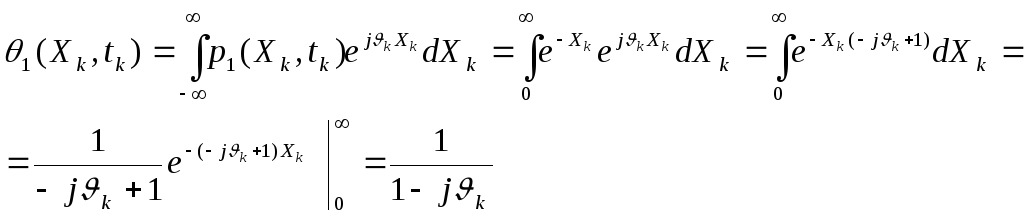
Початкове значення за означенням .

Наведені формули для визначення характеристичних функцій є справедливими як для неперервних, так І дискретних чи неперервно-дискретних процесів. В той же час для дискретних процесів представлення диференціальних законів розподілу через дельта функції дозволяє перехід від операції інтегрування при обчисленні характеристичних функцій до операції додавання. Зокрема, одновимірна характеристична функція 1-го порядку може бути обчислена за формулою:

де - можливі дискретні значення дискретного випадкового процесу в момент часу t_k, P(X_s) - ймовірності прийняття цих значень.

Приклад. Обчислити характеристичну функцію результату роботи ІВС для двох випадків:

1. випадкова фізична величина 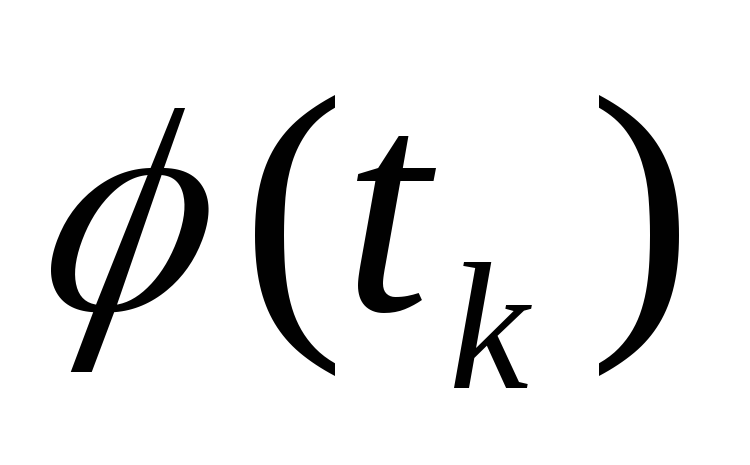приймає єдине значення А;

2. випадкова фізична величина приймає два значення: +А та -А;

У першому випадку ймовірність

Тоді

У другому випадку ймовірності значень +А і –А є однаковими.

Характеристична функція

Приклад.

Каналом зв’язку телевимірювальної ІВС, що знаходиться під дією завад, передається кодова комбінація з двох імпульсів. В результаті незалежної дії колений імпульс подавляється завадою з ймовірністю р.

Визначити характеристичну функцію, яка характеризує кількість подавлених завадою імпульсів.

Кількість подавлених імпульсів - дискретна випадкова величина, можливі значення якої:

Ймовірності кожного цих значень обчислимо за відомою із теорії ймовірності формулою:

де q = 1-p, n - кількість незалежних дослідів (в нашому випадку це кількість імпульсів у кодовій комбінації); k - число, яке визначає скільки разів здійсниться відповідна подія в серії із n незалежних дослідів. (кількість імпульсів, що може бути подавлена завадою: 0, 1, 2; - число сполучень із n величин по k .Відома формула

Згідно з ( ) і ( ) отримаємо такі значення для ймовірностей:

Остаточно характеристичну функцію знаходимо згідно з ( ).

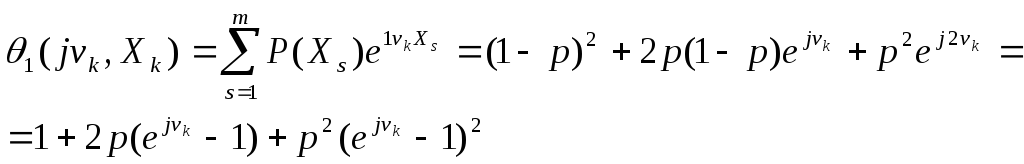
Приклад.

Наведемо ще один показовий приклад, що підтверджує особливий характер та місце нормального закону розподілу ймовірностей.

Для нормального закону з нульовим математичним очікуванням характеристична функція

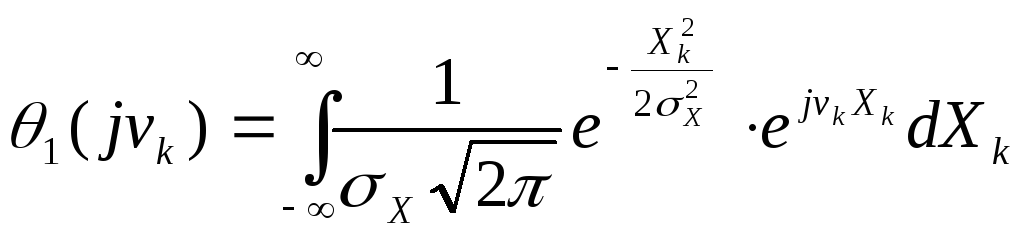
Обчислення інтегралів подібного типу здійснюється з використанням доповнення показника експоненти до повного квадрата:

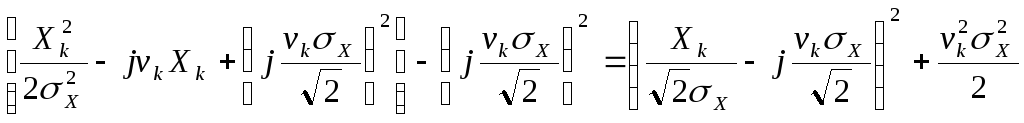
Введемо нову змінну

Тоді і згідно з ( ) та ( )

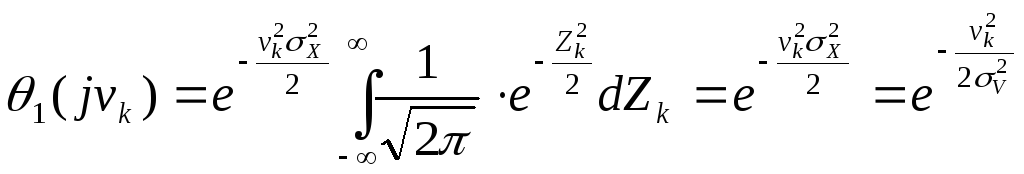
де враховано значення інтеграла, яке дорівнює одиниці, а також, що

Таким чином,

за нормального закону розподілу характеристична функція відносно v_k має таку ж форму, що і функція щільності ймовірностей відносно X_k .

Відповідно до останнього висновку про відхилення будь-якого закону розподілу ймовірностей від нормального можливо судити по тому, наскільки характеристична функція, що йому відповідає, відрізняється від ( ).

В чому ж полягає сутність методу характеристичних функцій.

Показано, що повна похибка системи

Будемо вважати, що є відомим, а також задані та , зокрема, функції щільності ймовірностей похибок основних блоків ІВС.

Характеристична функція ІВС послідовної структури

Відповідно до (1)

Якщо похибки блоків є некорельованими величинами, то математичне очікування добутку дорівнює добуткові математичних очікувань співмножників.

Характеристична функція суми некорельованих випадкових величин дорівнює добуткові їх характеристичних функцій.

Отже, для ІВС послідовної структури характеристична функція сумарної (повної) похибки дорівнює добуткові характеристичних функцій некорельованих похибок її блоків.

Зворотне перетворення Фур’є останньої дає закон розподілу ймовірностей повної похибки системи, на основі якого можна обчислити його числові статистичні характеристики, зокрема, середньостатистичне значення похибки, відхилення від нього чи дисперсію, довірчу ймовірність на основі заданого інтервалу – чи навпаки.

Приклад. За Лапласового закону розподілу похибок ВК і БО функція щільності ймовірностей похибок

Обчислимо її методом характеристичних функцій

За відомих законів розподілу ймовірностей похибок їх середньо?????? та дисперсії можна також знайти на основі характеристичних функцій