Контрольная работа

“ НЕОПРЕДЕЛЕННЫЙ И ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ”

1 Первообразная и неопределенный интеграл

При выполнении предыдущих контрольных работ мы столкнулись с тем, что ряд физических и геометрических задач сводится к нахождению производных от функций. Наряду с этим ряд задач сводится к обратной операции–отысканию функции по ее производной. Эта операция называется интегрированием, следовательно, интегрирование должно заключаться в следующем: задана производная –требуется найти функцию.

Определение. Функцию , заданную на промежутке , называют первообразной для функции , заданной на том же промежутке, если для всех выполняется равенство (или, что то же самое, равенство ). Например, для функции первообразной будет функция , т. к. для всех ; для функции первообразной будет функция , т.к. для всех ; для скорости точки первообразной будет путь , который прошла эта точка, т. к. , и так далее.

Так как первообразная имеет производную, следовательно, она непрерывна. Но верно и более глубокое утверждение: если функция непрерывна, то она имеет первообразную. В интегральном исчислении мы будем иметь дело только с непрерывными функциями.

Если функция является первообразной для функции на промежутке , то и любая из функций вида является первообразной для на том же промежутке. Это следует из того, что

.

Нетрудно убедиться в верности и обратного утверждения: если есть первообразная , то все первообразные для содержатся в формуле .

Определение. Совокупность всех первообразных для заданной функции на промежутке называется неопределенным интегралом этой функции и обозначается так: (читается: ”интеграл эф от икс дэ икс”);

• называется подынтегральной функцией;

• произведение – подынтегральным выражением;

• знаком интеграла;

• – переменной интегрирования.

Если есть первообразная для , то (C–произвольная константа). Например,

Из определения интеграла следует, что каждой формуле дифференциального исчисления соответствует формула в интегральном исчислении, так что в частности вся таблица производных может быть переписана в виде таблицы интегралов:

I. 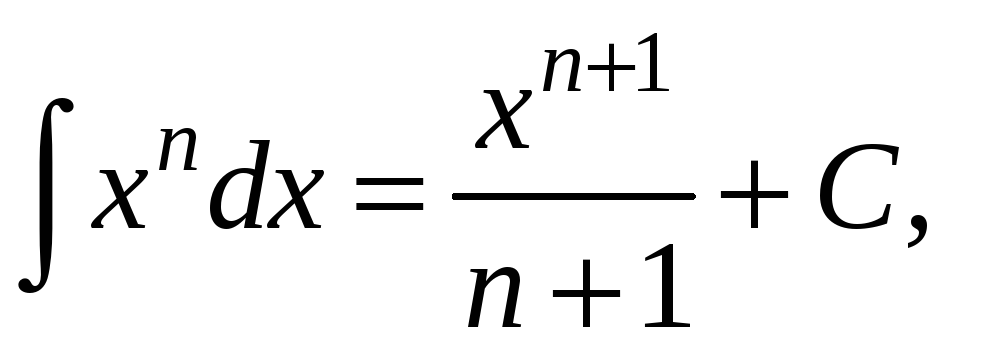где ; II. ;

III. ; IV. ;

V. ; VI. ;

VII. ; VIII. ;

IX. ; X. ;

XI. ; XII. ;

XIII. ; XIV. ;

XV. XVI..

Займемся теперь основными свойствами неопределенных интегралов и правилами их вычисления.

Примем без доказательства свойства неопределенного интеграла:

1.

2.

3.

4. ;

5. (k–постоянная);

6. .

1. Интегрирование подстановкой

Замена переменной (подстановка) в интеграл производится по формуле

; (1.1)

при этом говорят, что в интеграле слева сделана замена переменной (подстановка) . Формулой (1.1) можно пользоваться следующим образом: подобрать функцию так, чтобы, подставив вместо подынтегральное выражение, получить более простой интеграл.

Пример 1. Найти

Решение. С целью упрощения подынтегрального выражения положим . Отсюда ; ; ;; ; . Заменив всюду под интегралом на , получим

При вычислении воспользовались формулой

Пример 2. Найти

Решение. Заметим, что Целесообразно ввести переменную . Тогда ; ; . Заменив всюду под интегралом на , на , получим

Пример 3. Найти

Решение. Заметим, что , т.к.

. Целесообразно ввести переменную . Заменив всюду под интегралом на , на , получим

Пример 4. Найти

Решение. Заметим, что , т.к. . Целесообразно ввести переменную . Тогда . Заменив всюду под интегралом на , на ; получим

.

На основании вышеизложенного можно ввести формулу

, (1.2)

где – первообразная функции.

Тогда

Из формулы (1.2) получим

1. .

2. .

3. .
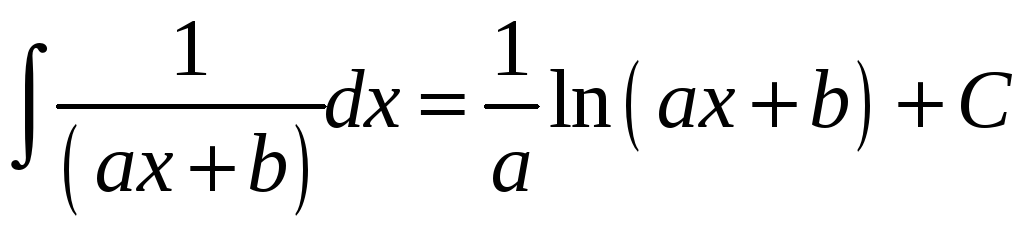