
- •Глава 6. Численные методы алгебры. Решение систем лИнейных уравнений
- •6.1. Линейные уравнения. Теоретическое и практическое решения линейных уравнений с одним неизвестным
- •6.2. Системы линейных уравнений. Основные понятия
- •6.3. Необходимое и достаточное условие существования решения системы линейных уравнений. Методы решения
- •6.4. Прямые методы решения систем линейных уравнений. Метод с использованием обратной матрицы и метод Крамера
- •6.5. Прямые методы решения систем линейных уравнений с исключением неизвестных. Метод Гаусса
- •6.5.1.Метод Гаусса.
- •6.6. Метод Гаусса-Жордана решения систем линейных уравнений
- •6.7.Решение систем линейных уравнений с использованием lu-разложения матрицы системы
- •6.7.1. Идея использования lu-разложения и алгоритм прямого метода расчета
- •6.7.2. Критерии существования lu-разложения. Трудоемкость и сложность его алгоритма
- •6.7.3. Решение системы линейных уравнений с использованием результатов lu-разложения ее матрицы.
- •6.8. Алгоритм расчета определителей с использованием исключения неизвестных
6.7.2. Критерии существования lu-разложения. Трудоемкость и сложность его алгоритма
Из общего вида расчетных формул (6.18.k.1)-(6.18.k.2) следует, что общим критерием, задающим необходимые и достаточные условия существования LU-разложения матрицы, является следующая совокупность неравенств:
u11 0, u22 0, u33(n-1) 0,…, u(n-1)(n-1) 0. (6.19)
Равенство unn = 0 может выполняться, поскольку на последнем шаге k=n не производится деления на диагональный элемент unn при расчете элементов матрицы L. Поэтому общий критерий выполняется и при det(A) 0 и при det(A) =0.
Отсутствие LU-разложения у исходной матрицы А не эквивалентно существованию единственного решения системы уравнений с матрицей А. Пример 1. Для матрицы порядка 2
![]()
единственное решение системы уравнений всегда (при любом свободном векторе B) существует, поскольку det(A) = -2 0. Но LU-разложения у матрицы А нет, поскольку у нее u11 = а11 = 0.
Общий критерий существования LU-разложения матрицы (6.19) не удобен для применения, так как требует почти полного расчета алгоритма (6.18.k.1)-(6.18.k.2). Поскольку наибольший интерес представляют случаи расчета LU-разложения матриц, когда соответствующие им системы имеют единственное решение (т.е. матрицы невырождены), то в этом случае критерий имеет более простой вид.
Теорема 6.1. (Критерий существования LU-разложение невырожденной матрицы). LU-разложение невырожденной матрицы А существует тогда и только тогда, когда:
а11 0. (6.20)
Доказательство. Так как 1) определитель произведения квадратных матриц одинакового порядка равен произведению их определителей и 2) определитель диагональной матрицы равен произведению ее диагональных элементов, то:
det(A) = det(L) det(U) =1 det(U) = u11 u22 u33 … unn . (6.21)
Необходимость. Если LU-разложение невырожденной матрицы А существует, то из (6.21) следует, что: u11u22u33…unn=det(A) 0, откуда вытекает справедливость общего критерия (6.19). Так как u11 = а11, то отсюда следует: а11 0.
Достаточность. Допустим, det(A) 0 и а11 0, но LU-разложение матрицы А не существует. Тогда по общему критерию (6.19) с учетом u11 = а11 0 следует, что нарушено неравенство нулю какого-либо из элементов в средней части главной диагонали матрицы U, т.е. существует ukk=0 при 2k(n-1). Но в этом случае из (6.21) следует, что det(U) = u11 u22 u33 … unn = det(A) = 0. Это противоречит условию невырожденности матрицы А. Полученное противоречие доказывает достаточность.
Пример 2. Выполнить LU-разложение квадратной матрицы А порядка n = 4:
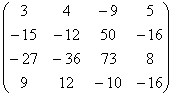 .
.
Решение. У матрицы а11 0. Вычисления производим по формулам (6.18.k.1)- (6.18.k.2) с проверкой значений ukk 0 при k = 1,...,n-1 = 3.
Шаг k = 1. u11 = а11 = 3 0, поэтому расчет продолжаем:
u12 = а12 = 4; u13 = а13 = -9; u14 = а14 = 5;
l11 =1; l21 = а21/ u11= -15/3 = -5; l31 = а31/ u11= -27/3 = -9; l41 = а41/ u11= 9/3 = 3.
Шаг k = 2. u21=0; u22 = а22 - l21 u12 = -12 - (-5)4 = 8 0, расчет продолжаем:
u23 = а23 - l21 u13 = 50 - (-5)(-9) = 5 ;
u24 = а24 - l21 u14 = -16 - (-5)5 = 9 ;
l12=0; l22=1; l32 = (а32 - l31 u12)/(u22) = (-36 - (-9)4)/8 = 0;
l42 = (а42 - l41 u12)/(u22) = (12 - 34)/8 = 0.
Шаг k = 3. u31=u32=0; u33 = а33 -(l31 u13 + l32 u23) = 73 - ((-9)(-9)+0) = -8 0, расчет продолжаем: u34 = а34 - (l31 u14 + l32 u24) = 8 - ((-9)5+0)= 53;
l13=0; l23=0; l33=1; l43 = (а43 - (l41 u13+ l42 u23))/u33 = ((-10) - (3(-9)+0))/(-8)= -17/8.
Шаг k = 4. u41=u42=u43=0;
u44 = а44 -(l41 u14 + l42 u24+ l43 u34) = (-16) - (35+0+(-17/8)53) = -31+901/8=653/8.
l14=0; l24=0; l34=0; l44=1.
В итоге получим матрицы:
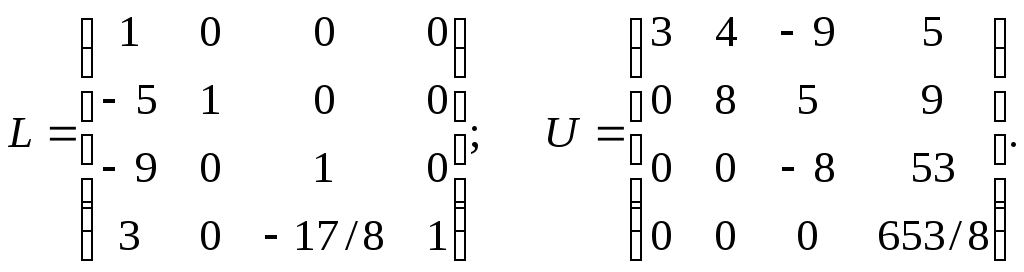
Трудоемкость и сложность алгоритма LU-разложения. Суммируя числа арифметических операций для расчета элементов матриц U и L, получим на каждом шаге k следующие их значения, используя вспомогательную величину k1 = (k-1):
- сравнений: сk(n) = 1;
- сложений и вычитаний: sk(n) = (k-1) (n - k+1) +(k-1) (n - k) = k1(2n -1) - 2k12;
- умножений: mk(n) = sk(n);
- делений: dk(n) = (n - k).
Трудоемкость всего алгоритма LU-разложения получим, суммируя числа операций для всех шагов k от 1 до n:
- сравнения: сLU(n) = n;
- сложения и вычитания: sLU(n) = (2n -1) [0+1+…+( n-1)] - 2[02+12+…+( n-1) 2] =
= n (n-1)(2n-1)/6 n3/3.
- умножения: mLU (n) = sLU (n) = n (n-1)(2n-1)/6 n3/3;
- деления: dLU (n) = [( n-1) +( n-1) +…1+0] = n(n-1)/2 n2/2.
По сравнению с алгоритмом прямого хода:
- число сравнений уменьшено на n(n-1)/2 n2/2;
- числа сложений (вычитаний), а также умножений уменьшены на:
n (n2-1)/3 - n (n-1)(2n-1)/6 = n (n-1)/6 n2/6;
- число делений осталось прежним.
Основную часть алгоритма составляют операции сложения (вычитания) и умножения, число которых расчет, как и у алгоритма прямого как n3/3. Сложность алгоритма LU-разложения равна О(n3).
