Правила Лопиталя

Рассмотрим способ раскрытия неопределенностей вида 0/0 и ∞ /∞ —, который основан на применении производных.

Теорема 4 (Правило Лопиталя раскрытия неопределенностей вида 0/0).

Пусть функции ƒ(х) и φ(x) непрерывны и дифференцируемы в окрестности точки х0 и обращаются в нуль в этой точке: ƒ(х0)=φ(х0)=0. Пусть φ'(х)¹ 0 в окрестности точки х0. Если существует предел

▲Применим к функциям ƒ(х) и φ(х) теорему Коши для отрезка [х0;х], лежащего в окрестности точки x0 . Тогда

где с лежит между х0 и х (рис. 144). Учитывая, что ƒ(х0)=φ(х0)=0, получаем

При х→х0, величина с также стремится к х0; перейдем в равенстве (25.4) к пределу:

Так как

Поэтому

Коротко полученную формулу читают так: предел отношения двух бесконечно малых равен пределу отношения их производных, если последний существует.

Замечания :

1. Теорема 4 верна и в случае, когда функции ƒ(х) и φ(х) не определены при х=х0, но

Достаточно положить

2. Теорема 4 справедлива и в том случае, когда х→∞. Действительно, положив х=1/z, получим

3. Если производные ƒ'(х) и φ'(х) удовлетворяют тем же условиям, что и функции ƒ(х) и φ(х), теорему 25.4 можно применить еще раз:

и. т. д.

Теорема 5 (Правило Лопиталя раскрытия неопределенностей вида ∞/∞).

Пусть функции ƒ(х) и φ(х) непрерывны и дифференцируемы в окрестности точки х0 (кроме, может быть, точки х0). в этой окрестности

φ'(х)¹ 0. Если существует предел

Раскрытие неопределенностей различных видов

Правило Лопиталя применяется для раскрытия неопределенностей вида 0/0 и ∞/∞, которые называют основными. Неопределенности вида 0•∞ ,∞-∞ , 1 ∞ , ∞ 0 , 0° сводятся к двум основным видам путем тождественных преобразований.

1. Пусть ƒ(х)→0, φ(х)→ ∞ при х→х0. Тогда очевидны следующие преобразования:

Например,

2. Пусть ƒ(х)→ ∞ , φ(х)→ ∞ при х→х0. Тогда можно поступить так:

На практике бывает проще, например,

3. Пусть или ƒ(х)→1 и φ(х)→ ∞ , или ƒ(х)→ ∞ и φ(x)→0, или ƒ(х)→0 и φ(х)→0 при х→х0. Для нахождения предела вида limƒ(х)φ(х) при х →х0 удобно сначала прологарифмировать выражение А=ƒ(х)φ(х).

Возрастание и убывание функций

Одним из приложений производной является ее применение к исследованию функций и построению графика функции.

Установим необходимые и достаточные условия возрастания и убывания функции.

Теорема 6 (необходимые условия). Если дифференцируемая на интервале (a;b) функция ƒ(х) возрастает (убывает), то ƒ'(х)≥0 (ƒ"(х)≤0) для " x є (a;b).

Пусть функция ƒ(х) возрастает на интервале (α;b). Возьмем произвольные точки х и х+∆х на интервале (α;b) и рассмотрим отношение

Функция ƒ(х) возрастает, поэтому если ∆х>0, то х+∆х>х и ƒ(х+∆х)>ƒ(х); если ∆х<0, то х+∆х<х и ƒ(х+∆х)<ƒ(х). В обоих случаях

так как числитель и знаменатель дроби имеют одинаковые знаки.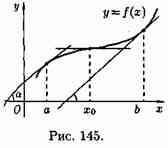

По условию теоремы функция ƒ(х) имеет производную в точке х и является пределом рассматриваемого отношения. Следовательно,

Аналогично рассматривается случай, когда функция ƒ (х) убывает на интервале (a;b).

Геометрически теорема 6 означает, что касательные к графику возрастающей дифференцируемой функции образуют острые углы с положительным направлением оси Ох или в некоторых точках (на рисунке 145 в точке с абсциссой х0) параллельны оси Ох.

Теорема 7 (достаточные условия). Если функция ƒ(х) дифференцируема на интервале (a;b) и ƒ'(х)>0 (ƒ'(х)<0) для " x є (a;b), то эта функция возрастает (убывает) на интервале (a;b).

Пусть ƒ'(х)>0. Возьмем точки х1 и х2 из интервала (a;b), причем x1<х2. Применим к отрезку [x1;x2] теорему Лагранжа: ƒ(х2)- ƒ(x1)=ƒ'(с)(х2-x1), где с є (x1;x2). По условию ƒ'(с)>0, х2-х1>0. Следовательно, ƒ(х2)-ƒ(х1)>0 или ƒ(х2)>ƒ(х1), т. е. функция ƒ(х) на интервале (a;b) возрастает.

Рассмотренные теоремы 6 и 7 позволяют довольно просто исследовать функцию на монотонность.