ВЫСШАЯ
МАТЕМАТИКА
Расчётно-графические задания
и методические указания к ним
для студентов заочного обучения всех специальностей
по темам:
Элементы линейной алгебры,
аналитическая геометрия,
теория пределов,
дифференциальное исчисление функции одной переменной
Данное пособие рассчитано на студентов заочной формы обучения и включает материал первого семестра: элементы линейной алгебры, аналитическая геометрия, теория пределов, дифференциальное исчисление функции одной переменной.
Учебное пособие предназначено для самостоятельного изучения теории и практики решения примеров. С этой целью, кроме соответствующих методических указаний, сообщается список необходимой литературы.
Каждую контрольную работу необходимо выполнять в отдельной тетради и подписывать ее по следующему образцу:
Контрольная работа № 1
по высшей математике
студента I курса группы _____
___________________________ факультета
Национального технического университета
"Харьковский политехнический институт"
Ф.И.О.
Дата отправки: ___________
Домашний адрес: __________
Подпись
Выполнять контрольную работу следует строго по своему варианту, в противном случае работа не проверяется.
Условия решаемых задач должны быть записаны полностью. Задачи нужно решать в порядке возрастания номеров, сохраняя номера, которые они имеют в методических указаниях. Решение задач должно иметь подробные объяснения.
Выполненные работы сдаются в деканат заочного обучения не позднее, чем за месяц до начала сессии. Получив проверенную работу, необходимо устранить допущенные ошибки. В конце работы следует заново записать условия и решения задач, имеющих ошибки. Исправленную работу необходимо сдать для проверки в кратчайший срок.
Соответствующая литература по материалу I-го семестра прилагается в конце учебного пособия.
Раздел 1 элементы линейной алгебры и аналитической геометрии
Перед выполнением контрольных заданий по этой теме необходимо изучить теоретический материал по учебникам.
Контрольные вопросы
1. Понятие матрицы. Действия над матрицами..
2. Определители Вычисление определителей.
3. Обратная матрица, ее вычисление.
4. Базисный минор и ранг матрицы. Элементарные преобразования матриц.
5. Понятие системы линейных алгебраических уравнений. Теорема Кронекера-Капелли.
6. Правило Крамера. Метод Гаусса.
7. Геометрические векторы. Декартова система координат. Действия над векторами, заданными в координатной форме.
8. Скалярное произведение, его свойства. Длина вектора. Угол между векторами.
9. Векторное произведение, его свойства. Смешанное произведение, его свойства. Геометрический смысл векторного и смешанного произведения.
10. Уравнение плоскости в координатной форме. Уравнение плоскости, проходящей через три точки.
11. Уравнение прямой на плоскости и в пространстве. Уравнение прямой, проходящей через две точки.
12. Угол между прямыми. Угол между прямой и плоскостью.
13. Кривые второго порядка. Эллипс, гипербола, парабола и их канонические уравнения.
14. Приведение общего уравнения кривой второго порядка к каноническому виду.
Ниже приведено решение типичных задач контрольных заданий с краткими методическими указаниями.
1.1. Элементы линейной алгебры
Задание 1.1
Рассматриваются действия над матрицами
Пример 1.1
Дано:
.
Найти:
а)
;
б)
,
где
;
Для решения примеров 1, а) и 1, б) введем некоторые понятия и определения.
1.
При умножении
матрицы на число
-
умножаются все элементы на число
.
2. При сложении матрицы одинаковой размерности складываются соответствующие элементы обеих матриц.
3.
Транспонированная
матрица
получается
из данной матрицы
,
если поменяются местами соответствующие
столбцы и строки.
4.
При умножении
матрицы
на
элементы
-ой
строки и
-го
столбца матрицы
находим по формуле:
.
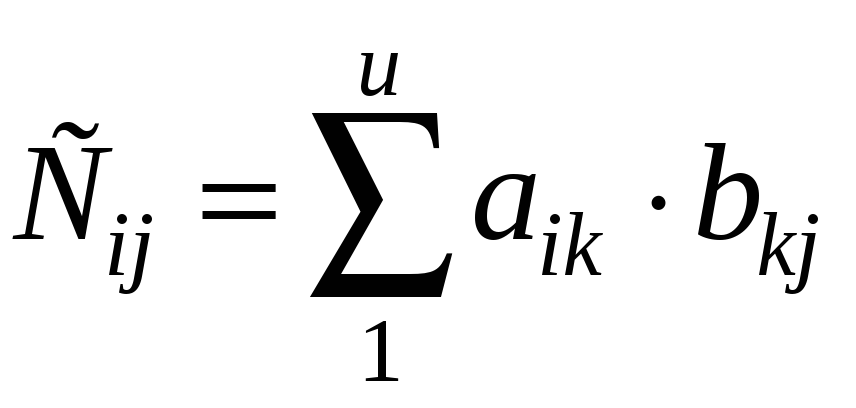Опираясь на пункты 1, 2, 3, 4 решим пример 1.
а) 1)
, 2)
.
Пусть
,
тогда
;
таким
образом,
.
3) 
.
Ответ:
.
б)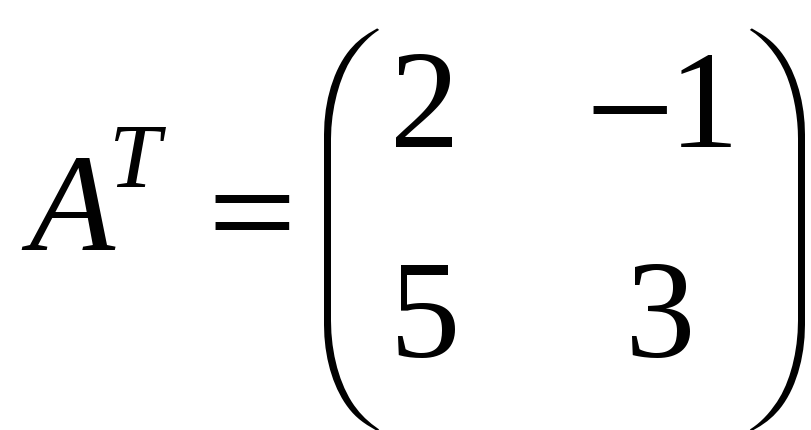 
; 
;
; 
;
Ответ:
.
Задание 1.2
Определители
второго порядка
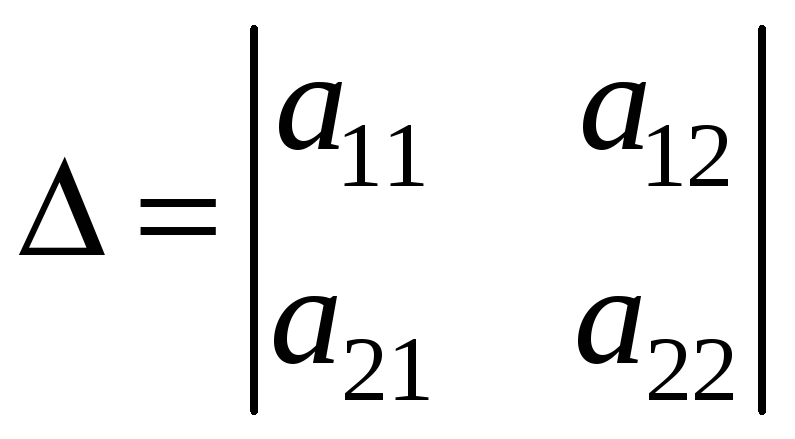вычисляются по формуле
.
Пример 1.2
; 
.
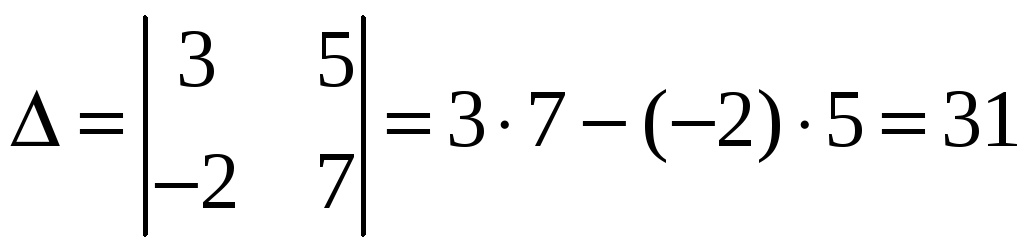Если
определитель размерности
,
где
,
то можно применять различные способы
вычисления. Рассмотрим некоторые из
них на примере определителя третьего
порядка:
.
Рассмотрим следующие два способа.
1) Правило “треугольников”:
Пример
1.3
; 
.
2) Раскладываем определитель по элементам первой строки
.
Решим пример 3 по второму способу:
;
; 
.
Задание 1.3
Пусть
дана матрица
размерности
:
.
Чтобы
найти матрицу
,
обратную данной, найдём:
1)
;
если
матрица А-1
существует;
2) транспонированную матрицу
;
3) союзную матрицу
;
где
- алгебраические дополнения, соответствующие
элементам
;
4)
искомую матрицу 
.
Пример 1.4
Дано:
Найти: А-1.
Решение:
1)
.
2)
; 3)
.
Чтобы
найти
,
вычёркиваем
-ую
строку и
-ый
столбец матрицы
и полученный определитель умножаем на
:
; 
; 
;
; 
; 
;
; 
; 
.
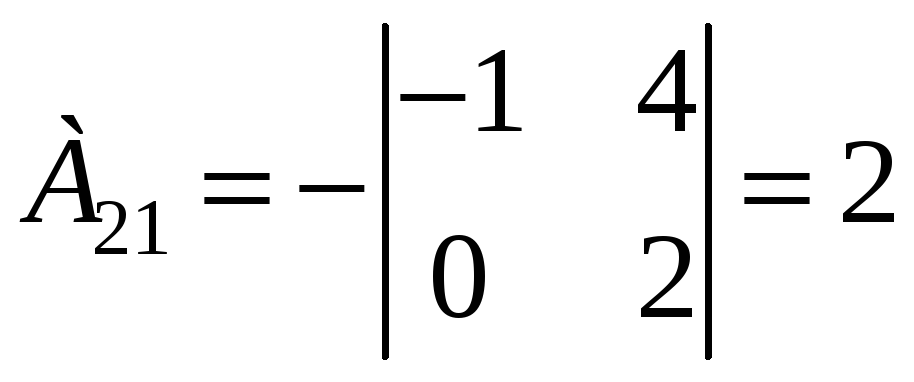Таким
образом,
.
4)
.
Ответ:
.
Задание 1.4
Решить систему: а) по формулам Крамера;
б) с помощью обратной матрицы.
Пример 1.5
Дана
система:
Формулы
Крамера:
,
где
- определитель системы, составленный
из коэффициентов при неизвестных. Он
равен:
(см. пример 3).
Определители
,
,
получаются из
путем замены соответствующего столбца
столбцом свободных членов системы:
;
;
.
Таким
образом,
;
;
.
Ответ:
.
Рассмотрим
решение примера 5 с помощью обратной
матрицы. Запишем данный пример матричным
способом:
где
,
,
.
Так
как
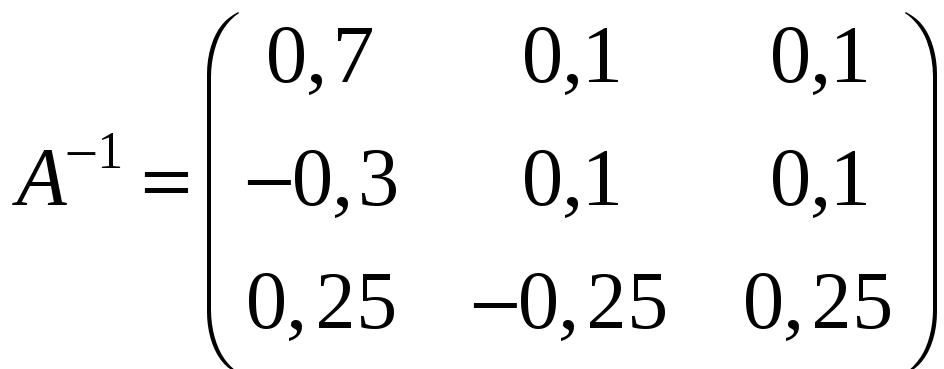(см. пример 4),
то
.
Ответ:
.
Задание 1.5
Исследовать систему на совместность и решить ее методом Гаусса.
Пусть
дана система размерности
:
(*)
Для исследования системы (*) на совместимость и её решения введём понятие о ранге матрицы и сформулируем теорему Кронекера - Капелли.
Если
в матрицы
размерности
взять какие-то
строк и
столбцов
и составить определители
-го
порядка, то эти определители называются
минорами
-го
порядка данной матрицы.
Определение.
Рангом матрицы
называется порядок наибольших отличных
от нуля миноров этой матрицы.
Пример 1.6
Найти ранг матрицы:
.
Решение.
Проделаем над матрицей
элементарные преобразования, которые
не меняют
ранга матрицы, а именно, отнимем от
второй строки первую, умножив её на 4;
затем отнимем от третей строки первую,
умножив её на 3:
.
Согласно
определению ранга матрицы, можно
утверждать,
что
,
т.к. все миноры
третьего порядка равны нулю, а хотя бы
один минор второго порядка, например
.
Теорема
Кронекера - Капелли.
Для того чтобы система (*) была совместна,
необходимо и достаточно чтобы
,
где
.
1)
Если
где,
-
число неизвестных, то система (*) имеет
единственное решение;
2)
если
- система имеет бесчисленное множество
решений;
3)
если
– система (*) несовместна и решения не
имеет.
Пример 1.7
Исследовать систему на совместность и решить ее методом Гаусса:
Запишем
матрицы
и
вместе и найдём их ранги: (
-номера
строк матриц
и
.)
Так
как
,
то
система
имеет бесчисленное множество решений.
Проделав “обратный ход”, запишем
систему:
так
как неизвестных четыре, а уравнений
два, то пусть
- “свободные” неизвестные, a
и
выразим через
,
где
и
- любые числа:
; 
Ответ:
.
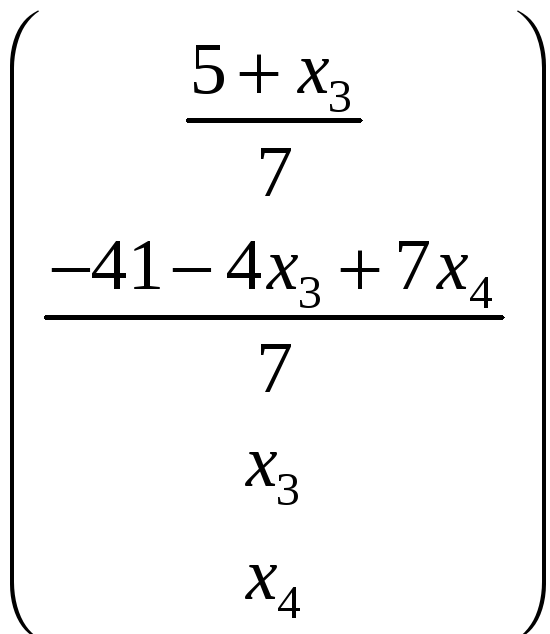в
частности, например, при
;
и
,
имеем:
;
,
то есть частное решение имеет вид
.
Проверьте самостоятельно, что частное
решение удовлетворяет системе примера
6.