МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ

ВОСТОЧНОУКРАИНСКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ

имени ВЛАДИМИРА ДАЛЯ

В.Ф. Пожидаев

ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

(методические указания)

Луганск, 2002

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ

ВОСТОЧНОУКРАИНСКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ

имени ВЛАДИМИРА ДАЛЯ

В.Ф. Пожидаев

ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

(методические указания)

Рекомендовано

кафедрой прикладной математики факультета математики и информатики

Восточноукраинского национального университета имени Владимира Даля

Ответственный за выпуск: В.М. Грибанов, проф.

Пожидаев В.Ф. Теория веротностей и математическая статистика. (методические указания). – Луганск: изд-во ВНУ им. В. Даля, 2002. – 101 с.

В данных методических указаниях представлены наборы ндивидуальных заданий, а также примеры их решений, рассчитаные на два учебных семестра изучения дисциплины теории вероятностей и математической статистики.

Индивидуальные задания рассчитаны на студентов II курса факультета математики и информатики.

Министерство образования и науки украины восточноукраинский национальный университет им. В. Даля

Проверил

Индивидуальное задание №1 ______________________

оценка: ____(__________)

Индивидуальное задание №2 ______________________

оценка: ____(__________)

Индивидуальное задание №3 ______________________

оценка: ____(__________)

Индивидуальное задание №4 ______________________

оценка: ____(__________)

Индивидуальное задание №1

Решение типового варианта.

1. Из различных книг , , , , отбирают 3 книги. Выпишите пространство элементарных событий, отвечающее этому эксперименту. Считая исходы эксперимента равновозможными, найдите вероятность того, что набор отобранных книг включает: а) книги и ; б) книгу ; в) либо книгу , либо .

Решение. Выбрать книги можно способами. Пространство элементарных событий:

а) – «книги и »:

.

б) – «книга А»:

в) – «книги или »:



Ответ: а) 0,3; б) 0,6; в) 0,9.

2. На отрезке [0,1] наудачу ставят две точки. Пусть и – координаты этих точек. Рассматриваются следующие события: {вторая точка ближе к левому концу отрезка, чем первая точка к правому}; {корни уравнения действительны}; ; .

Найти: .

Решение.

;

;

;

;

а )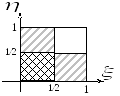

б)

в )

Ответ: а) 0,75; б) 0; в) 0,79.

3. Наудачу выбирают последовательно 2 цифры. Опишите:

1) пространство элементарных исходов; 2) событие – “среди выбранных двух чисел нет нуля”; 3) событие – “все цифры различные”; 4) событие – “цифры образуют двузначное число”. Найти вероятности событий , , и определить, какие из этих событий являются несовместными.

Решение. Зададим пространство элементарных исходов таблицей. Всего способов.

	0	1	2	3	4	5	6	7	8	9
0	00	01	02	03	04	05	06	07	08	09
1	10	11	12	13	14	15	16	17	18	19
2	20	21	22	23	24	25	26	27	28	29
3	30	31	32	33	34	35	36	37	38	39
4	40	41	42	43	44	45	46	47	48	49
5	50	51	52	53	54	55	56	57	58	59
6	60	61	62	63	64	65	66	67	68	69
7	70	71	72	73	74	75	76	77	78	79
8	80	81	82	83	84	85	86	87	88	89
9	90	91	92	93	94	95	96	97	98	99

– «среди чисел есть 0»;

: .

– «цифры одинаковые»:

: .

– «число не является двузначным»

: .

Несовместных событий нет, так как:

и совместны, так как среди чисел, не содержащих «0», есть числа с разными цифрами.

и совместны, так как в данном случае все числа, не содержащие «0», являются двузначными.

и совместны, так как среди двузначных чисел есть числа с разными цифрами.

Ответ: ; ; .

4. Число грузовых автомашин, проезжающих по шоссе, на котором стоит бензоколонка, относится к числу легковых, проезжающих по тому же шоссе, как 3:5. Известно, что в среднем одна из 30 грузовых и 2 из 50 легковых машин подъезжают к бензоколонке для заправки. Чему равна вероятность того, что: а) подъехавшая к бензоколонке машина будет заправляться; б) на заправке стоит легковая автомашина; в) на заправке стоит грузовая автомашина?

Решение. Событие – «машина будет заправляться»: для грузовых – , для легковых – .

Число проезжающих по шоссе машин: грузовых – , легковых – , всего – .

Пусть событие – «грузовая машина», – «легковая машина». Тогда:

, , , .

а) .

б)

в)

Ответ: а) 0,02; б) 0,78; в) 0,23.

5. а) пусть вероятность того, что телевизор потребует ремонта в течение гарантийного срока, равна 0,2. Найти вероятность того, что в течение гарантийного срока из 4 телевизоров: а) не более 1 потребует ремонта; б) хотя бы один потребует ремонта;

Решение. Применим формулу Бернулли: .

; .

а) , ; ;

;

.

б) Найдем вероятность того, что не сломается ни один телевизор:

: ; .

Ответ: а) 0,8192; б) 0,5904.

б) оптовая база обслуживает 18 магазинов. От каждого из них заявка на товары на следующий день может поступить с вероятностью 0,4. Найти наивероятнейшее число заявок на следующий день и вероятность получения базой 4 заявки.

Решение. , , .

Применим предельную теорему Пуассона: , где . .

Найдем наивероятнейшее число заявок: .

Ответ: ; .

в) вероятность попадания в цель при каждом выстреле равна 0,001. Найти вероятность попадания в цель двумя и более выстрелами при залпе из 5000 ружей.

Решение. Найдем вероятность попадания в цель менее, чем двумя выстрелами. Применим формулу Пуассона:

, , , , .

, , ,

Ответ: 0,96.

г) всхожесть пшеницы 90%. Сколько нужно высеять зерен, чтобы абсолютная величина отклонения частоты всходов от вероятности всхода отдельного зерна с вероятностью 0,95 не превышала 0,05?

Решение. ; ; .

Применим следующую формулу:

;

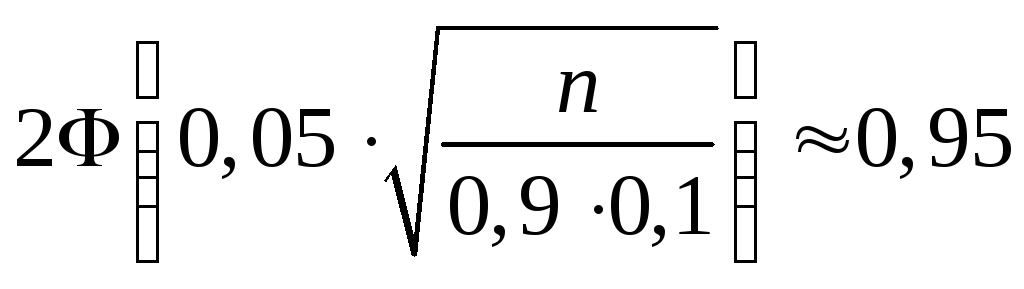
133.

Ответ: 133.

6. В этой задаче по поставленному или заданному закону распределения дискретной случайной величины вычислить ее математическое ожидание, дисперсию, среднее квадратическое отклонение, а также начертить ее многоугольник распределения и график функции распределения.

Имеется 5 различных ключей, из которых только один подходит к замку. Составить закон распределения числа опробований при открывании замка ключей, если испробованный ключ в последующих попытках открыть замок не участвует.

Решение. Для вычисления вероятности применим геометрический закон распределения. – с какого раза подошел ключ

Распределение дискретной случайной величины:

X	1	2	3	4	5
P	0,2	0,2	0,2	0,2	0,2

Найдем

Найдем математическое ожидание:

Найдем дисперсию:

Найдем среднеквадратическое отклонение:

Многоугольник распределения: Функция распределения:

6. Случайная величина задана функцией плотности распределения . Найти:

1) функцию распределения и необходимые константы;

2) математическое ожидание, дисперсию и среднее квадратическое отклонение;

3) вероятность попадания случайной величины в интервал . Построить графики функций распределения и плотности распределения .

Решение.

1. Найдем константу:

Найдем :

:

:

: .

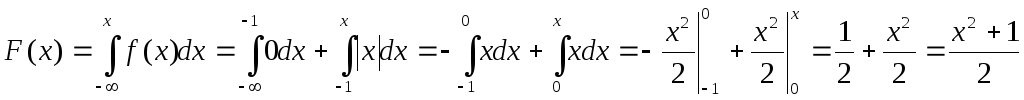
2. Найдем математическое ожидание:

Найдем дисперсию:

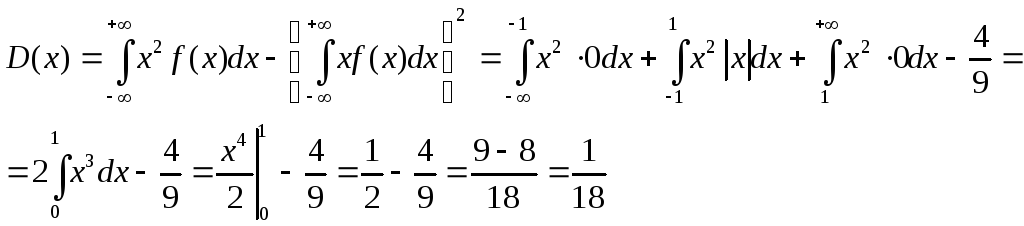
Найдем среднеквадратическое отклонение:

3. Найдем вероятность попадания в интервал :

, где – среднеквадратическое отклонение; – математическое ожидание.

0.043

Построим графики функций и :

Вариант – 1

1.1. Для лечения некоторой хронической болезни применяются 5 лекарств a,b,c, d,e. Врач хочет провести сравнительное исследование трех из этих пяти лекарств. Три исследуемых лекарства врач отбирает из данных пяти случайным образом. Чему равна вероятность того, что: а) лекарство а будет исследовано? б) будут исследованы лекарства а и b? в) будет исследовано, по крайней мере, одно из лекарств a и b?

2.1. На отрезке [0,1] наудачу ставят две точки. Пусть и - координаты этих точек. Рассматриваются следующие события:

A = {вторая точка ближе к левому концу отрезка, чем первая точка к правому}; B = {корни уравнения действительны}; C = {max {} }; D = {min {}}.

Найти: P(AB), P(A\C), P(B\D).

3.1. Каждый из трех пассажиров с равной вероятностью может сесть в любой из 4 вагонов пассажирского поезда. Описать : а) пространство элементарных исходов распределения пассажиров по вагонам; б) событие А - “все трое попали в первый вагон”; в) событие В - “трое пассажиров попали в первые пять вагонов”; г) событие С - “трое пассажиров попали в разные вагоны”; д) событие D - “трое пассажиров попали в один вагон”. Найдите вероятности событий A,B,C,D. Покажите, какие из этих событий являются попарно несовместными.

4.1. Для участия в студенческих отборочных соревнованиях выделено из первой группы 4 студента, из второй - 6, из третьей - 5 студентов. Вероятности того, что отобранный студент из первой, второй, третьей группы попадет в сборную института, равны соответственно 0,5; 0,4 и 0,3. Какова вероятность того, что наудачу взятый студент попадет в сборную? Если студент попал в сборную, то к какой из трех групп он вероятнее всего принадлежит?

5.1. а) фарфоровый завод отправил на базу 10000 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равна 0,0001. Найти вероятность того, что на базу придут ровно 3 негодных изделия;

б) вероятность изготовления стандартной детали равна 0,9. Какова вероятность того, что среди 10 деталей окажется не более 1 нестандартной ?

в) батарея дала 140 выстрелов по военному объекту, вероятность попадания в который равна 0,2. Найти наивероятнейшее число попаданий и его вероятность;

г) мастерская по гарантийному ремонту телевизоров обслуживает 2000 абонентов. Вероятность того, что купленный телевизор потребует гарантийного ремонта, равна 0,3. Найти границы числа телевизоров, которые потребуют гарантийного ремонта, если вероятность отклонения частоты телевизоров, требующих ремонта, от теоретической вероятности, не превысит 0,9974.

6.1. Составить закон распределения вероятностей случайной величины Х, представляющей собой число появления события А в 5 независимых испытаниях, если вероятность появления события в каждом испытании равна 0,6. Найти вероятность того, что событие А появится не менее 2 раз.

7.1. Случайная величина  задана функцией плотности распределения f(x). Найти:

1) функцию распределения F(x) и необходимые константы;

2) математическое ожидание, дисперсию и среднее квадратическое отклонение;

3) вероятность попадания случайной величины  в интервал ().

Построить графики функций распределения F(x) и плотности распределения f(x).

,  = - /, = - /12.

Вариант – 2

1.2. В старинной индийской игре “Тонг” два игрока одновременно показывают друг другу либо один, либо два, либо три пальца на правой руке. Если для каждого игрока равновозможно показать один, два или три пальца, чему равна вероятность того, что общее число показанных пальцев четно ?, Нечетно? Простое?

2.2. На отрезке [0,1] наудачу ставят две точки. Пусть и - координаты этих точек. Рассматриваются следующие события:

A= {вторая точка ближе к левому концу отрезка, чем первая точка к правому}, B = { корни уравнения действительны }, C = { max {}  }; D = { min {} }.

Найти: P(A\B), P(AC), P(BD).

3.2. Двенадцать мест стоянки автомобилей расположены в один ряд. На стоянке случайным образом размещены 8 автомобилей. Описать:

а) пространство элементарных исходов размещения автомобилей; б) событие А - “4 пустых места следуют одно за другим”; в) событие В - “3 пустых места следуют одно за другим”. Найти вероятности событий А и В. Являются ли эти события несовместными и независимыми? Найдите P(AB), P(A\B), P(B\A).

4.2. На сборку попадают детали, изготовленные тремя автоматами. Известно, что первый автомат дает 0,4 % брака, второй - 0,2 и третий - 0,6 %. Найти вероятность попадания на сборку бракованной детали, если с первого автомата поступило 500, со второго - 1000 и с третьего - 1250 деталей. Если деталь оказалась бракованной, то какой из трех автоматов ее вероятнее всего изготовил?

5.2. а) сколько нужно проверить деталей, чтобы с вероятностью: 0,9; 0,99; 0,999 можно ожидать, что абсолютная величина отклонения частоты годных деталей от вероятности 0,9 того, что деталь окажется годной, не превысит 0,01 ( по абсолютной величине )?

б) на факультете 730 студентов. Вероятность того, что студент не придет на занятия, равна 0,1. Найти наивероятнейшее число студентов, не явившихсяна занятия, и вероятность этого события;

в) принимая вероятности рождения мальчика и девочки одинаковыми, найти вероятность того, что среди 6 новорожденных двое окажутся мальчиками;

г) вероятность того, что изделие не выдержит испытания, равна 0,001. Найти вероятность того, что из 5000 изделий более чем одно не выдержит испытания.

6.2. Из урны, содержащей 4 белых и 4 черных шара, наугад извлекают три шара. Пусть X - число вынутых черных шаров. Построить ряд распределения случайной величины X.

7.2. Случайная величина  задана функцией плотности распределения f(x).

Найти: 1) функцию распределения F(x) и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение, вероятность попадания случайной величины  в интервал (). Построить графики функций распределения F(x) и плотности распределения f(x).

, .

Вариант – 3

1.3. Из ящика, содержащего три билета с номерами 1,2,3, вынимают по одному билету. Предполагается, что все последовательности номеров билетов имеют одинаковые вероятности. Найти вероятность того, что : а) у одного билета порядковый номер совпадает с собственным; б) у двух билетов порядковый номер совпадает с собственным.

2.3. На отрезке [0,1] наудачу ставят две точки. Пусть и - координаты этих точек. Рассматриваются следующие события:

A= { вторая точка ближе к левому концу отрезка, чем первая точка к правому }, B = { корни уравнения действительны }, C = { max {}  }; D = { min {} }.

Найти: P(B\A), P(AD), P(BC).

3.3. Из цифр 0,1,...,9 образуют всевозможные двузначные числа. Опишите: а) пространство элементарных событий; б) событие А - “числа образованы из различных цифр”; в) событие В - “числа образованы из одинаковых цифр”; г) событие С - “в двузначном числе обе цифры четные”; д) событие D - “в двузначном числе обе цифры нечетные”; е) событие Е - “в двузначном числе отсутствует 0, а обе цифры - четные”. Найти вероятность всех перечисленных событий. Являются ли события: А и В, С и Е несовместными, а события D и Е - независимыми?

4.3. Из урны, содержащей 3 белых и 2 черных шара, переложен один вынутый наудачу шар в урну, содержащую 4 белых и 5 черных шаров. Найти вероятность того, что шар, наудачу вынутый из второй урны, окажется белым. Если вынутый из второй урны шар оказался белым, то какова вероятность того, что из первой урны был переложен : а) белый шар; б) черный шар?

5.3. а) оптовая база обслуживает 12 магазинов. От каждого из них заявка на товары на следующий день может поступить с вероятностью 0,3. Найти наивероятнейшее число заявок на следующий день и вероятность получения базой такого числа заявок;

б) вероятность выхода конденсатора из строя в течение времени t равна 0,25. Вычислить вероятность того, что за этот промежуток времени из имеющихся 150 конденсаторов выйдет из строя от 40 до 80;

в) устройство состоит из 1000 элементов, работающих независимо один от другого. Вероятность отказа любого элемента в течение времени t равна 0,002. Найти вероятность того, что за время t откажут ровно 3 элемента;

г) пусть вероятность того, что автомат сработает неправильно, равна 0,3. Найти наивероятнейшее число случаев неправильной работы автомата при 150 испытаниях. Какова вероятность того, что автомат не сработает такое количество раз?

6.3. Охотник, имеющий 5 патронов, стреляет в цель до первого попадания или пока не израсходует все патроны. Вероятность попадания при каждом выстреле равна 0,8. Составить закон распределения случайной величины Х, представляющей число израсходованных патронов.

7.3. Случайная величина  задана функцией плотности распределения f(x). Найти : 1) функцию распределения F(x) и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины  в интервал (). Построить графики функций распределения F(x) и плотности распределения f(x).

, .

Вариант – 4

1.4. Сделано три выстрела по мишеням. Пусть событие Аi - “при i-м выстреле произошло попадание в мишень”, i = 1,2,3. Опишите пространство элементарных событий этого опыта. Считая исходы опыта равновозможными, найдите вероятность события А, предварительно выразив его через Аi, если: а) А - “произошло три попадания”; б) А- “не было ни одного попадания”; в) А - было ровно одно попадание”.

2.4. На отрезке [0,1] наудачу ставят две точки. Пусть и - координаты этих точек. Рассматриваются следующие события:

A= {вторая точка ближе к левому концу отрезка, чем первая точка к правому}, B = {корни уравнения действительны}, C = {max {} }, D = {min {}}.

Найти: P(АВ), Р(АD), Р(ВС).

3.4. Из корзины, содержащей 4 пронумерованных от 1 до 4 шара, последовательно берут 2 шара без возврата. Опишите пространство элементарных исходов этого опыта, элементами которого являются двузначные числа, полученные из номеров последовательно извлеченных двух шаров. Описать элементарные исходы: а) события А - “среди вынутых шаров есть шар с цифрой 3”; б) событие В - “сумма цифр на шарах делится на 3”. Являются ли эти события: а) несовместными; б) независимыми? Найдите вероятность этих событий Р(А) и Р(В), а также Р(АВ) и Р(АВ).

4.4. Пассажир может обратиться за получением билета в одну из трех касс. Вероятности попадания в каждую кассу зависят от их местонахождения и равны соответственно 0,2; 0,5; 0,3. Вероятности того, что в кассах все билеты проданы, равны соответственно 0,6; 0,9; 0,7. Какова вероятность того, что пассажир приобретет билет? Если пассажир приобрел билет, то в какой из трех касс он вероятнее всего купил билет?

5.4. а) вероятность выпуска бракованного сверла 0,02. Сверла укладываются в коробки по 1000 штук. Найти вероятность того, что в коробке окажется два бракованных сверла.

б) вероятность допущения дефектов при производстве механизмов равна 0,4. Наудачу отбиратся 500 механизмов. Установить величину наибольшего отклонения относительной частоты изготовленных механизмов с дефектами от вероятности 0,4, которую можно гарантировать с вероятностью 0,998.

в) Сколько изделий первого сорта с вероятностью 0,0315 можно ожидать в партии из 1000 наудачу взятых изделий, если вероятность появления изделия первого сорта в отдельном испытании равна 0,8?

г) вероятность того, что расход электроэнергии на протяжении одних суток не превысит установленной нормы, равна 0,8. Найти вероятность того, что: а) в ближайшие 5 суток расход электроэнергии в течение 3 суток не превысит нормы; б) в течение 2 суток превысит норму.

6.4. Из ящика,содержащего 2 бракованных и 4 годных детали наугад извлекают 4 детали. Пусть Х - число вынутых годных деталей. Построить ряд распределения случайной величины Х.

7.4. Случайная величина  задана функцией плотности распределения f(x). Найти : 1) функцию распределения F(x) и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3). вероятность попадания случайной величины  в интервал (). Построить графики функций распределения F(x) и плотности распределения f(x).

,

Вариант – 5

1.5. У малыша в кармане алтын (3 коп.), пятак (5 коп.), гривенник (10 коп.), полтинник (50 коп.). Он вынимает из кармана одну за одной две монеты. Выпишите пространство событий. Чему равна вероятность того, что мальчик вынул менее 20 копеек? Чему равна вероятность того, что число, выражающее ценность извлеченных монет, делится на 5? Что это число простое?

2.5. На отрезке [0,1] наудачу ставят две точки. Пусть и - координаты этих точек. Рассматриваются следующие события:

A= { вторая точка ближе к левому концу отрезка, чем первая точка к правому }, B = { корни уравнения действительны }, C = { max {}  }; D = { min {} }.

Найти: P(АВ), Р(С\В), Р(D\A).

3.5. В распоряжении агрохимика есть шесть типов минеральных удобрений. Он изучает совместное влияние каждой тройки удобрений на опытном участке площадью 1 га. Опишите пространство элементарных исходов. Какая площадь должна быть занята опытными участками, если все возможные эксперименты проводятся одновременно? Опишите элементарные исходы события А - “тройка удобрений, содержащая удобрения второго и пятого типа” и события В - “тройка удобрений, содержащая удобрения третьего типа”. Найти Р(А), Р(В), Р(А+В). Независимы ли события А и В?

4.5. С 1-го станка на сборку поступает 40 %, со 2-го - 30% и с 3-го - 30% всех деталей. Вероятность изготовления бракованной детали для каждого станка соответственно равна 0,01; 0,03; 0,05. Найдите вероятность того, что наудачу поступившая на сборку деталь бракованная. С какого станка вероятнее всего поступит на сборку бракованная деталь?

5.5. а) вероятность неточной сборки прибора равна 0,2. Произведена сборка 500 приборов. Найти наивероятнейшее количество неточно собранных приборов и вероятность появления такого события;

б) вероятность нарушения герметичности банки в некоторой партии консервных банок равна 0,0004. Вычислить вероятность того, что среди 2000 банок окажутся с нарушением герметичности не более 3;

в) при штамповке металлических клемм получается в среднем 90 % годных. Найти вероятность того, что среди 900 клемм окажется от 700 до 820 годных.

г) в семье 5 детей. Найти вероятность того, что среди этих детей 2 мальчика. Вероятность рождения мальчика принять равной 0,51.Чему равна вероятность того, что в семье хотя бы 1 мальчик?

6.5. Из каждой партии телевизоров для контроля извлекают 4 телевизора и последовательно их проверяют. При появлении плохо работающего телевизора бракуется вся партия. Пусть Х - количество проверенных телевизоров до появления бракованного, и вероятность брака равна 0,2. Составить закон распределения случайной величины Х.

7.5. Случайная величина  задана функцией плотности распределения f(x).

Найти: 1) функцию распределения F(x) и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины  в интервал (). Построить графики функций распределения F(x) и плотности распределения f(x).

, .

Вариант – 6

1.6 Задумано некоторое двузначное число. Какова вероятность того, что: а) сумма цифр этого числа будет равна 6; б) число делится на 6 ?

2.6 На отрезке [0,1] наудачу ставят две точки. Пусть и - координаты этих точек. Рассматриваются следующие события:

A= { вторая точка ближе к левому концу отрезка, чем первая точка к правому }, B = { корни уравнения действительны }, C = { max {}  }; D = { min {} }.

Найти: P(АВ), Р(С\В), Р(D\A).

3.6 Технология предусматривает обработку детали последовательно на трех станках одного типа и двух станках другого типа с непрерывным чередованием видов станков. Станки распределены случайно. Опишите: а) пространство элементарных исходов распределения станков в ряд; б) событие А - “станки распределялись согласно технологии”; В - “станки распределялись по типам: в начале одного типа, затем все станки другого типа”. Найдите Р(А) и Р(В). Совместны ли эти события?

4.6 Известно, что 5 % всех мужчин, 0,25 % всех женщин дальтоники. Считая, что мужчин и женщин одинаковое число, определить вероятность того, что случайно выбранное лицо страдает дальтонизмом. Какова вероятность того, что дальтоник оказался: а) мужчиной; б) женщиной ?

5.6 а) вероятность случайным образом отобранному изделию оказаться стандартным, равна 0,8. Найти вероятность того, что среди 225 взятых наугад изделий 180 окажутся стандартными;

б) вероятность появления брака при автоматической обработке деталей равна 0,003. Найти вероятность того, что среди 1000 деталей только 4 детали будут бракованными;

в) вероятность выигрыша по 1 билету лотереи - 1/7. Какова вероятность того, что лицо, имеющее 6 билетов, выиграет: по 2 билетам; по 3 билетам; не выиграет по 2 билетам;

г) было посажено 400 деревьев. Вероятность того, что отдельное дерево приживется, равна 0,8. Найти вероятность того, что число прижившихся деревьев  250.

6.6 В колоде осталось 7 карт, из них 3 козырных. Наугад выбирают 4 карты. Пусть Х - число взятых козырных карт. Построить ряд распределения случайной величины Х.

7.6 Случайная величина  задана функцией плотности распределения f(x).

Найти : 1) функцию распределения F(x) и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины  в интервал (). Построить графики функций распределения F(x) и плотности распределения f(x).

.

Вариант – 7

1.7. Найти вероятность того, что минимальный выигрыш (т.е. угадано по 3 числа) придется на обе карточки “Спортлото” с отмеченными номерами (4, 12, 38, 20, 41, 46) и (4, 12, 38, 20, 41, 49).

2.7. На отрезке [0,1] наудачу ставят две точки. Пусть икоординаты этих точек. Рассматриваются следующие события:

А={вторая точка ближе к левому концу отрезка, чем первая точка к правому}; В={корни уравнения х²+2x+действительны}; С={max{} < ½}; D={min{} < ½}. Найти: Р((AВ)ВС)), Р(А).

3.7. На 10 карточках написаны буквы, составляющие слово “астрономия”. Выбирается 5 карточек. Опишите: а)”пространство элементарных исходов”; б) событие А -”получилось слово “мотор”; в)событие В - “получилось слово “ситро”. Определить вероятности событий А и В. Рассмотреть два случая: а) карточки выставляются в порядке извлечения; б) извлеченные карточки можно переставлять.

4.7. Часы изготавливаются на трех заводах и поступают в магазин. Первый завод производит 40% продукции, второй - 45%, третий - 15%. В продукции первого завода спешат 80% часов, второго -70%, третьего -90%. Какова вероятность того,что купленные часы не спешат? Если купленные часы спешат, то на каком заводе они вероятней всего изготовлены?

5.7. а) вероятность того, что в партии встретится бракованная деталь,равна 0,2. Какова вероятность того, что из 5 деталей бракованных будет менее 2?

б) пусть вероятность того, что покупателю необходима обувь 41 размера, равна 0,2. Найти вероятность того, что из 750 покупателей только 120 потребуют обувь этого размера;

в) вероятность промышленного содержания металла в каждой пробе руды равна 0,4. Считая, что событие, вероятность которого 0,997, достоверно, найти границы числа проб с промышленным содержанием металла среди 1000 проб;

г) молокозавод отправил в магазин 1000 пакетов молока. Вероятность повреждения пакета во время транспортировки равна 0,0005. Вычислить вероятность того, что количество поврежденных пакетов не превысит 3.

6.7. Из урны, содержащей 4 белых и 4 черных шара последовательно извлекают шары до появления первого белого шара,не возвращая их обратно в урну. Составить закон распределения случайной величины Х - числа извлеченных черных шаров.

7.7. Случайная величина задана функцией плотности распределения f(x). Найти: 1) функцию распределения F(x) и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины в интервал (Построить график функции распределения F(x) и плотности распределения f(x).

, .

Вариант – 8

1.8 Два шара - красный и синий - помещают в три ящика, пронумерованных числами 1,2 и 3. Выпишите соответствующее этому эксперименту пространство событий, если оба шара можно положить в один ящик. Чему равна вероят-ность того, что: а) хотя бы один ящик будет пустым ? б) только один ящик будет заполнен шарами ?

2.8 На отрезке [0,1] наудачу ставят две точки. Пусть и - координаты этих точек. Рассматриваются следующие события:

A= { вторая точка ближе к левому концу отрезка, чем первая точка к правому }, B = { корни уравнения действительны }, C = { max {}  }; D = { min {} }.

Найти: P(СD), Р(ВD), Р(АС).

3.8 На полку ставят четырехтомное собрание сочинений М.Ю. Лермонтова. Описать: а) пространство элементарных исходов расстановки книг; б) событие А - “в начале стоит первый том, в конце - четвертый”; в) событие В - “в середине стоят по порядку 2-й и 3-й тома”. Найдите вероятности событий А и В. Являются ли эти события совместными и независимыми ? Найдите Р(АВ) и Р(А\В).

4.8 На некоторой фабрике машина А производит 40 % продукции, а машина В - 60 % продукции. В среднем 9 единиц из 10000 единиц продукции, произведенных машиной А, и 1 единица из 250 единиц продукции, произведенных машиной В, оказываются бракованными. Какова вероятность того, что единица продукции, выбранная случайным образом из всей дневной продукции фабрики, оказалась бракованной? На какой машине вероятнее всего будет изготовлена бракованная продукция?

5.8 а) вероятность рождения мальчика равна 0,515. Найти вероятность того, что среди 100 новорожденных окажется 50 мальчиков; б) в хлопке имеется 10 % коротких волокон. Какова вероятность того, что в наудачу взятом пучке из 4 волокон окажется не более 2 коротких?

в) средний процент нарушения работы кинескопа телевизора в течение гарантийного срока равен 22. Вычислить вероятность того, что из 46 наблюдаемых телевизоров более 36 выдержат гарантийный срок;

г) радиоаппаратура состоит из 1000 электроэлементов. Вероятность отказа одного элемента в течение одного года работы равна 0,001 и не зависит от состояния других элементов. Какова вероятность отказа двух и не менее двух электроэлементов за год?

6.8 В ящике имеется 10 носовых платков, 2 из которых имеют монограмму “0”, 3 - монограмму “С”, 5 - монограмму “Т”. Наугад извлекают три платка. Пусть случайная величина Х представляет число вынутых платков с монограммой “О”. Построить ряд распределения случайной величины Х.

7.8 Случайная величина  задана функцией плотности распределения f(x). Найти : 1) функцию распределения F(x) и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины  в интервал (). Построить графики функций распределения F(x) и плотности распределения f(x).

, .

Вариант – 9

1.9 Игральная кость бросается дважды. Опишите пространство элементарных событий этого эксперимента, если его элементами служат суммы выпавших очков. Введите элементарные вероятности, считая равновозможными выпадения любой пары очков. Найдите вероятности событий А - “сумма очков больше 10”; В - “сумма очков делится на два”.

2.9 На отрезке [0,1] наудачу ставят две точки. Пусть и - координаты этих точек. Рассматриваются следующие события:

A= { вторая точка ближе к левому концу отрезка, чем первая точка к правому }, B = { корни уравнения действительны }, C = { max {}  }; D = { min {} }

Найти: P(СD), Р(ВС), Р(АD).

3.9 Из города А в город В можно добраться четырьмя дорогами. Из В в С ведут две дороги, из С в D - три дороги. Расстояния между двумя соседними пунктами дороги имеют различную длину. Путешественник выбирает дорогу в каждом пункте произвольно.

Опишите пространство элементарных исходов и найдите вероятность того, что путешественник пойдет из А в D : а) по самой короткой дороге; б) по самой длинной дороге.

4.9 Из урны, содержащей 3 белых и 2 черных шара, вынуты наудачу 2 шара и переложены в урну, содержащую 4 белых и 4 черных шара. Из второй урны наудачу выбирают шар. Чему равна вероятность того, что он белый? Если из второй урны извлечен белый шар, то наиболее вероятно какого цвета шары извлечены из первой урны и переложены во вторую?

5.9 а) по данным длительной проверки качества выпускаемых запчастей определенного вида брак составляет 13 %. Определить вероятность того, что в непроверенной партии из 150 запчастей пригодных будет 128 штук;

б) визуальное наблюдение искусственного спутника Земли возможно в данном пункте с вероятностью 0,1 (отсутствие облачности ). Проводится 100 попыток наблюдения спутника. Найти практически достоверный диапазон числа удачных наблюдений ( с вероятностью Р = 0,9975 );

в) вероятность изготовления стандартной детали равна 0,9. Какова вероятность того, что среди 10 деталей окажется не более 1 нестандартной?

г) при проверке 10000 пар мужских носков обнаружено 200 пар с дефектами. Какова вероятность того, что в партии из 300 пар число дефектных носков будет не более 5?

6.9 В цехе имеется 5 однотипных станков. Вероятность выхода из строя одного станка равна 0,8. Пусть случайная величина Х равна количеству станков, потребовавших ремонта. Составить закон распределения этой случайной велины.

7.9 Случайная величина  задана функцией плотности распределения f(x).

Найти: 1) функцию распределения F(x) и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины  в интервал (). Построить графики функций распределения F(x) и плотности распределения f(x).

, .

Вариант - 10

1.10 Два бруска - черный и белый - представляют собой правильные четырех-угольные призмы. Боковые грани этих брусков пронумерованы числами 1,2,3 и 4. Бруски покатили по полу и после их остановки заметили числа на верхних гранях брусков. Постройте таблицу для пространства событий, отвечающего этому эксперименту. Если х - номер верхней грани черного брус-ка, а у - номер верхней грани белого бруска, то найдите : а) Р(х+у = 5); б) Р(х = у); в) Р(х  у+1).

2.10 На отрезке [0,1] наудачу ставят две точки. Пусть и - координаты этих точек. Рассматриваются следующие события:

A= { вторая точка ближе к левому концу отрезка, чем первая точка к правому }, B = { корни уравнения действительны }, C = { max {}  }; D = { min {} }.

Найти: P(СD), Р(ВD), Р(АС).

3.10 Из корзины, содержащей 4 занумерованных от 1 до 4 шара, последовательно берут два шара с возвратом после каждого извлечения. Опишите пространство элементарных исходов этого опыта, если его элементами являются двузначные числа, полученные из номеров последовательно вынутых шаров; описать элементарные исходы события А - “сумма цифр на вынутых шарах делится на 3”; событие В - “сумма цифр на вынутых шарах делится на 2”. Являются ли эти события: а) несовместными; б) независимыми? Найти Р(А) и Р(В), а также Р(АВ), Р(АВ), Р(А\В).

4.10 В группе спортсменов 18 лыжников, 8 велосипедистов и 4 бегуна. Вероятность выполнить квалификационную норму такова: для лыжника - 0,9; для велосипедиста - 0,8; для бегуна - 0,75. Найти вероятность того, что спортсмен, выбранный наудачу, выполнит норму. Если спортсмен выполнил квалификационную норму, то какова вероятность того, что этим спортсменом будет: а) лыжник; б) велосипедист; в) бегун?

5.10 а) вероятность выигрыша по одному билету равна 1/3. Какова вероятность того, что лицо, имеющее шесть билетов: выигрывает по двум билетам; выигрывает по трем билетам; не выигрывает по двум билетам;

б) при установившемся технологическом процессе фабрика выпускает 80 % первосортной продукции. Найти вероятность того, что в партии из 400 изделий 330 будут первого сорта;

в) в партии из 1000 изделий имеется 10 дефектных. Найти вероятность того, что среди 50 изделий, взятых наудачу из этой партии, ровно три окажутся дефектными;

г) в некоторой местности имеется 3% больных малярией. Произведено обследование 500 человек. С какой вероятностью среди обследованных окажется от 2,5% до 3,5% больных?

6.10 Имеется 9 радиоламп, среди которых 3 неисправных. Наугад берутся 4 радиолампы и проверяются на годность. Построить ряд распределения случайной величины Х, представляющей собой количество неисправных радиоламп.

7.10 Случайная величина  задана функцией плотности распределения f(x). Найти : 1) функцию распределения F(x) и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины  в интервал (). Построить графики функций распределения F(x) и плотности распределения f(x).

, .

Вариант - 11

1.11 Из букв слова “плюс” наугад выбирают две буквы одну за другой. Выпишите пространство элементарных событий для этого эксперимента. Какова вероятность того, что: а) выбранная пара букв не содержит гласной? б) гласная буква выбрана первой?

2.11 На отрезке [0,1] наудачу ставят две точки. Пусть и - координаты этих точек. Рассматриваются следующие события:

A= { вторая точка ближе к левому концу отрезка, чем первая точка к правому }, B = { корни уравнения действительны }, C = { max {}  }; D = { min {} }.

Найти: P(АВС), Р((АВ)D).

3.11 Два лица х и у рассаживаются вместе с 8 остальными произвольным обра-зом за круглым 10-местным столом. Описать: а) пространство элементарных исходов размещения этих лиц; б) событие А - “лица х и у оказались рядом”; в) событие В - “между лицами х и у находится один человек”. Найдите Р(А) и Р(В). Являются ли события А и В зависимыми, несовместными?

4.11 На фабрике станки 1-й, 2-й и 3-й производят соответственно 20, 35, 45 % всех изделий. В их продукции брак составляет соответственно 6, 4, 2 %. Какова вероятность того, чтослучайно выбранное изделие оказалось дефектным? Какова вероятность того, что оно было произведено: а) станком 1; б) станком 2; в) станком 3?

5.11 а) всхожесть семян некоторого растения составляет 70 %. Какова вероятнос-того, что из 10 посеянных семян взойдут : 8; по крайней мере 8; не менее 8?

б) при автоматической прессовке карболитовых болванок 2/3 общего числа из них не имеют зазубрин. Найти вероятность того, что из 450 взятых наудачу болванок, количество болванок без зазубрин заключено между 280 и 320;

в) производство электронно-лучевых трубок для телевизоров дает в среднем 12 % брака. Найти вероятность наличия 215 годных трубок в партии из 250 штук;

г) на базу поступило 10000 электроламп. Вероятность того, что в пути лампа разобьется, равна 0,0003. Найти вероятность того, что среди полученных ламп пять ламп разбито.

6.11 Пусть случайная величина Х представляет число очков, выпавших при одном бросании игральной кости. Составить закон распределения этой случайной величины. Какова вероятность того, что при пяти бросаниях игральной кости 2 очка выпадет 3 раза ?

7.11 Случайная величина  задана функцией плотности распределения f(x). Найти : 1) функцию распределения F(x) и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины  в интервал (). Построить графики функций распределения F(x) и плотности распределения f(x).

, .

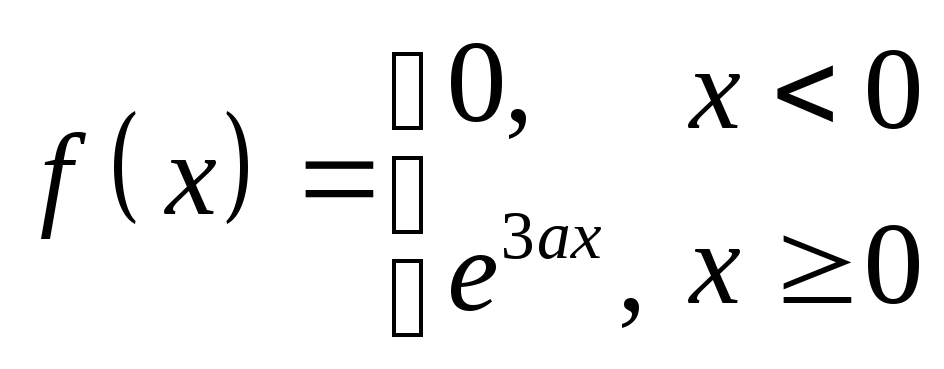Вариант - 12

1.12 Числа 1, 2, 3 и 4 написаны на четырех карточках. Наудачу последовательно выбирают две карточки, и вынутые таким образом цифры ставятся слева направо. Опишите пространство элементарных событий этого опыта. Чему равна вероятность того, что полученное таким образом двузначное число: а) окажется четным? б) простым? в) кратным трем?

2.12 На отрезке [0,1] наудачу ставят две точки. Пусть и - координаты этих точек. Рассматриваются следующие события:

A= { вторая точка ближе к левому концу отрезка, чем первая точка к правому }, B = { корни уравнения действительны }, C = { max {}  }; D = { min {} }.

Найти: P(АВС), Р((АВ)D).

3.12 Магазин принимает партию из 10 радиоприемников, если при проверке двух из них, выбранных наугад, оба оказываются исправными. В магазин поступила партия, содержащая 4 неисправных радиоприемника. Опишите: а) пространство элементарных событий, получаемых при выборе двух радиоприемников; б) событие А - “два проверяемых радиоприемника исправны”; в) событие В - “из двух проверяемых радиоприемников один неисправен”. Найдите вероятность того, что магазин примет партию при 4 неис-правных радиоприемниках - Р(А) и Р(В). Можно ли сказать, что события А и В несовместны, независимы?

4.12 Прибор, установленный на борту самолета, может работать в двух режимах: в условиях нормального крейсерского полета и в условиях перегрузки при взлете и посадке. Крейсерский режим полета осуществляется в 80 % всего времени полета, условия перегрузки - в 20 %. Вероятность выхода прибора из строя за время полета в нормальном режиме равна 0,1, в условиях перегрузки - 0,4. Вычислить надежность прибора за время полета. Если прибор вышел из строя, то какова вероятность того, что это произошло: а) в крейсерском режиме полета; б) в условиях перегрузки?

5.12 а) вероятность попадания в цель при одном выстреле равна 0,4. Найти вероятность того, что цель будет поражена 100 раз из 320 выстрелов;

б) вероятность изготовления на автоматическом станке стандартной детали равна 0,9. Определить вероятность того, что из трех наудачу взятых деталей: 2 окажутся стандартными; стандартными окажутся все 3;

в) найти вероятность того, что в партии из 800 изделий отклонение числа изделий 1-го сорта от наивероятнейшего числа не превысит по абсолютной величине 50, если вероятность появления изделия первого сорта Р = 0,7;

г) найти вероятность того, что среди 200 изделий окажется более трех бракованных, если в среднем бракованные изделия составляют 1 %.

6.12 Производится тестирование 5 больших интегральных схем (БИС). Вероятность того, что БИС неисправна, равна 0,6. Построить ряд распределений случайной величины Х, представляющей собой количество неисправных БИС.

7.12 Случайная величина  задана функцией плотности распределения f(x). Найти : 1) функцию распределения F(x) и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины  в интервал (). Построить графики функций распределения F(x) и плотности распределения f(x).

, .

Вариант - 13

1.13 Бросается игральная кость и катится брусок, представляющий собой правильную четырехугольную призму, боковые грани которой пронумерованы числами 1, 2, 3 и 4. После чего записываются числа, отвечающие их верхним граням. Постройте таблицу, в которую входят все элементарные события для этого эксперимента. Если х - число очков на верхней грани кости, а у - число очков на боковой грани бруса, найдите : а) Р(х+у = 6), б) Р(х  у), в) Р(х+у - нечетное число).

2.13 На отрезке [0,1] наудачу ставят две точки. Пусть и - координаты этих точек. Рассматриваются следующие события:

A= { вторая точка ближе к левому концу отрезка, чем первая точка к правому }, B = { корни уравнения действительны }, C = { max {}  }; D = { min {} }.

Найти:P(АВD), Р((АВ)\С).

3.13 Из цифр 1, 2, 3, 4, 5 составляют всевозможные трехзначные числа с неповторяющимися цифрами. Описать : а) пространство элементарных исходов; б) событие А - “числа составлены из цифр 1, 2, 3”; в) событие В - “число четное”; г) событие С - “число нечетное”; д) событие D - “число делится на четыре”. Найдите вероятности событий А, В, С, D . Выясните, какие из этих событий являются несовместными, независимыми.

4.13 В ящике лежат 20 теннисных мячей, в том числе 15 новых и 5 - уже бывших в игре. Для игры наудачу выбираются 2 мяча и после игры возвращаются обратно. Затем для второй игры также наудачу извлекаются еще 2 мяча. Какова вероятность того, что второй игры будут взяты новые мячи? Если для второй игры были взяты новые мячи, то какова вероятность того, что для первой игры были взяты : а) старые мячи; б) один старый, один новый; в) новые мячи?

5.13 а) в цехе 5 моторов. Для каждого мотора вероятность того, что он в данный момент включен, равна 0,8. Найти вероятность того, что в данный момент включено не менее 2 моторов.

б) в опыте Бюффона монета подбрасывалась 4040 раз. При этом “герб” выпал 2048 раз. С какой вероятностью можно было ожидать этот результат?

в) устройство состоит из 1600 элементов, работающих независимо один от другого. Вероятность отказа любого элемента в течение времени t равна 0,001. Найти вероятность того, что за время t откажут не более 10 элементов.

г) вероятность наступления события в каждом из независимых испытаний постоянна и равна 0,6. Сколько испытаний необходимо произвести, чтобы вероятность отклонения частоты от 0,6 в ту и другую сторону менее, чем на 0,01 была равна 0,995?

6.13 Пусть Х - количество очков, выпавших при бросании 2 игральных костей. Построить ряд распределения этой случайной величины.

7.13 Случайная величина  задана функцией плотности распределения f(x). Найти : 1) функцию распределения F(x) и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины  в интервал (). Построить графики функций распределения F(x) и плотности распределения f(x).

, .

Вариант - 14

1.14 Два стрелка дважды выстрелили по мишеням. Опишите пространство элементарных событий этого опыта. Введите элементарные вероятности, если для первого стрелка вероятность попадания в цель 0,9, для второго - 0,8. Найдите вероятность события А , если : а) А - “произошло два попадания”; б) А - “произошло хотя бы одно попадание”; в) А - “произошло менее трех попаданий”.

2.14 На отрезке [0,1] наудачу ставят две точки. Пусть и - координаты этих точек. Рассматриваются следующие события:

A= { вторая точка ближе к левому концу отрезка, чем первая точка к правому }, B = { корни уравнения действительны }, C = { max {}  }; D = { min {} }.

Найти: P(АВС), Р((АВ)D).

3.14 Из нечетных цифр составлены всевозможные двузначные числа. Наудачу извлекается одно число. Опишите: 1) пространство элементарных исходов; 2) событие А - “извлеченное число делится на 3”; 3) событие В - “извлеченное число делится на 5”; 4) событие С - “извлеченное число содержит цифру 5”. Найти вероятности событий А, В, С, D, А+В, В\А, ВС, АВС. Являются ли события С и А\В независимыми?

4.14 Вероятность для изделий некоторого производства удовлетворять стандарту, равна 0,96. Предлагается упрощенная система испытаний, дающая положительный результат с вероятностью 0,98 для изделий, которые не удовлетворяют стандарту, с вероятностью 0,95 для изделий, удовлетворяющих стандарту. Какова вероятность того, что наудачу выбранное изделие будет удовлетворять стандарту? Если изделие признано удовлетворяющим стандарту, то какова вероятность того, что: а) изделие все же не удовлетворяет стандарту; б) действительно удовлетворяет стандарту?

5.14 а) вероятность изготовления детали на автоматическом станке равна 0,9. Найти вероятность того, что из 8 взятых наудачу деталей не менее 7 окажутся стандартными;

б) взято 800 проб руды. Вероятность промышленного содержания металла в каждой пробе одинакова и равна 0,3. С вероятностью, равной 0,997, найти границы числа проб с промышленным содержанием металла во взятой партии проб;

в) какова вероятность того, что среди 200 человек будет 6 левшей, если левши в среднем составляют 1%;

г) устройство состоит из 1500 элементов, работающих независимо один от другого. Вероятность отказа каждого из них в течение времени t равна 0,0017. Найти вероятность того, что за время t откажут от 2 до 4 элементов.

6.14 Пусть Х - количество “гербов”, полученных при бросании 3 монет. Составить закон распределения этой случайной величины.

7.14 Случайная величина  задана функцией плотности распределения f(x). Найти : 1) функцию распределения F(x) и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины  в интервал (). Построить графики функций распределения F(x) и плотности распределения f(x).

.

Вариант - 15

1.15 Из числа трех мужчин (Андрей, Борис, Виктор) и двух женщин (Галина, Дарья) собирается комиссия из трех человек. Опишите пространство элементарных событий этого эксперимента. Чему равна вероятность того, что членом комиссии будет хотя бы одна женщина; хотя бы один мужчина?

2.15 На отрезке [0,1] наудачу ставят две точки. Пусть и - координаты этих точек. Рассматриваются следующие события:

A= { вторая точка ближе к левому концу отрезка, чем первая точка к правому }, B = { корни уравнения действительны }, C = { max {}  }; D = { min {} }.

Найти: P(АВС), Р((АВ)D).

3.15 В лотерее из 10 билетов 3 выигрышных. Некто купил 2 билета. Опишите: а) пространство элементарных исходов при покупке 2-х билетов; б) событие А - “оба билета выигрышные”; в) событие В - “ни один из билетов не выигрышный”; г) событие С - “среди купленных билетов ровно один выигрышный”. Являются ли события А, В, С несовместными, независимыми ? Чему равна сумма событий А, В и С ? Найдите Р(А), Р(В), Р(С), Р(А+С).

4.15 В продажу поступают телевизоры трех заводов. Продукция первого завода содержит 20 % телевизоров со скрытым дефектом, второго - 10 %, третьего - 5 %. Какова вероятность приобрести исправный телевизор, если в магазин поступило 30 % телевизоров с 1-го завода, 20 % - со 2-го и 50 % - с 3-го. Если телевизор исправен, то какой завод вероятнее всего его изготовил?

5.15 а) устройство состоит из 400 элементов, работающих независимо один от другого. Вероятность отказа любого элемента, проработавшего время t, равна 0,15. Найти наивероятнейшее количество приборов, которые могут отказать через время t, и вероятность отказа такого количества;

б) рабочий обслуживает три станка. Вероятность того, что в течение смены станок потребует его внимания, равна 0,7. Найти вероятность того, что в течение смены внимания рабочего потребуют два станка; хотя бы один станок;

в) вероятность наступления события в каждом испытании равна 0,8. Найти наибольшее отклонение частоты этого события от вероятности его наступления, которое можно ожидать с вероятностью 0,9146 при 4600 испытаниях;

г) прядильщица обслуживает 1000 веретен. Вероятность обрыва нити на 1 веретене в течение 1 минуты равна 0,003. Вычислить вероятность того, что в течение 1 минуты произойдет не более двух обрывов.

6.15 В лотерее разыгрываются мяч стоимостью 3 руб., шахматы стоимостью 10 руб., кеды стоимостью 5 руб. Общее число билетов равно 20. Пусть случайная величина Х представляет размер выигрыша в рублях. Составить закон распределения случайной величины Х.

7.15 Случайная величина  задана функцией плотности распределения f(x). Найти : 1) функцию распределения F(x) и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины  в интервал (). Построить графики функций распределения F(x) и плотности распределения f(x).

Вариант - 16

1.16 Из обычной колоды (в 36 игральных карт) извлекается одна за другой две карты. Пусть упорядоченная пара (х,у) обозначает отвечающее этому эксперементу элементарное событие: здесь х есть наименование вынутой карты, а у - наименование второй. Тогда а) сколько элементарных событий образует пространство событий? б) чему равна вероятность того, что первая карта туз, а вторая валет?

2.16 На отрезке [0,1] наудачу ставят две точки. Пусть икоординаты этих точек. Рассматриваются следующие события:

А={вторая точка ближе к левому концу отрезка, чем первая точка к правому}; В = { корни уравнения х²+2x+действительны}; С = {max{}  ½}; D={min{}  ½}.

Найти:Р(АВС), Р((АВ)D).

3.16 Из ящика, содержащего 8 красных и 4 синих шаров, наудачу извлекают 3 шара. Опишите: а) пространство элементарных исходов; б) событие А - “ все извлеченные шары красные”; в) событие В - “все извлеченные шары синие “; г) событие С - “среди извлеченных шаров один синий и два красных”; д) событие D - “среди извлеченных шаров два синих и один красный”; е) событие Е - “среди извлеченных шаров не более двух красных”. Является ли события А, В, С, D, Е попарно несовместными и попарно независимыми? Можно ли из этих событий получить полную систему событий? Найдите вероятности этих событий.

4.16 В первой урне находятся 1 белый и 9 черных шаров, а во второй 1 черный и 5 белых шаров. Из каждой урны по схеме случайного выбора без возвращения удалили по 1 шару, а оставшиеся шары ссыпали в 3-ю урну. Найти вероятность того, что шар, вынутый из 3-й урны, окажется белым. Если, вынутый из 3-й урны, шар оказался белым, то какое событие более вероятно: из первой и второй удалили по одному белому или из 1-й удалили белый, а из 2-й - черный?

5.16 а) вероятность попадания в цель составляет при отдельном выстреле 0,8. Найти вероятность того от 2 до 4 попаданий при 6 выстрелах;

б) вероятность наступления события в каждом из одинаковых и независимых испытаний равна 0,2. Найти вероятность того, что в 150 испытаниях событие наступит 5 раз;

в) в каждой из 1000 урн находится 5000 белых и 5000 черных шаров. Из каждой урны извлекают без возвращения 3 шара. Чему равна вероятность того, что число урн, из которых извлекли одноцветные шары, заключено между 220 и 300?

г) в зрительном зале находится 400 человек. Какова верояность того, что среди них имеются 3 левши, если левши в среднем составляют 1% ?

6.16 В ящике 100 шаров, из них 20 синих, 30 черных и 50 красных. Шар вынимают наугад, фиксируют его цвет и возвращают в ящик. Проводится 6 таких испытаний. Пусть случайная величина Х - количество вынутых черных шаров в этих испытаниях. Составить закон распределения этой случайной величины.

7.16 Случайная величина задана функцией плотности распределения f(x). Найти: 1) функцию распределения F(x) и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины в интервал (

Построить график функции распределения F(x) и плотности распределения f(x).

при , .

Вариант - 17

1.17 На книжной полке в случайном порядке стоит энциклопедический справочник, состоящий из 4-х томов. Какова вероятность того, что хотя бы один из томов этого справочника стоитна своем месте? Только 2 тома стоят на своем месте?

2.17 На отрезке [0,1] наудачу ставят две точки. Пусть икоординаты этих точек. Рассматриваются следующие события:

А={вторая точка ближе к левому концу отрезка, чем первая точка к правому}; В={корни уравнения х²+2x+действительны}; С={max{} < ½}; D={min{} < ½}. Найти: Р(AВD), Р((АВ)С).

3.17 Вгруппе учащихся 10 девушек и 6 юношей для работы наудачу выбирают 5 человек. Опишите: а) пространство элементарных исходов, получаемое при выборе 5 человек; б) событие А - “выбраны только юноши”; в) событие В - “выбраны только девушки”; г) событие С - “ среди выбраных не более одного юноши”. Является ли события А, В, С, D попарно несовместными и попарно независимыми? Какие события представляют полную систему событий? Найдите вероятности событий А, В, С, D.

4.17 На сборку поступают детали с двух автоматов. Первый дает в среднем 0,2% брака, второй - 0,1%. Найти вероятность попадания на сборку бракованой детали, если с первого автомата поступило 2000 деталей, а со второго - 3000. Если деталь бракованная, то какой автомат вероятнее всего ее изготовил?

5.17 а) рабочий обслуживает 4 станка. Каждый станок в течение 8 часов работы простаивает из-за поломки 0,8 часа, причем остановки в любой момент времени равновероятны. Определить вероятность того, что в данный момент времени простаивает менее 2 станков;

б) из большой партии продукции, содержащей 70% изделий 1-го сорта, наугад отбирают 100 изделий. вычислить вероятность того, что среди отобраных будет 75 изделий 1-го сорта;

в) вероятность попадания в мишень при каждом из 700 выстрелов равна 0,4. Какое максимально возможное отклонение от вероятности попадания при отдельном выстреле равна 0,4. Какое максимально возможное отклонение от вероятности попадания при отдельном выстреле можно ожидать с вероятностью 0,997?

г) предположим, что в озере было 15000 рыб, причем 1000 из них меченых. Из озера отловлено 150 рыб. Какое среднее возможное число меченых среди отловленых и чему равна вероятность такого числа?

6. 17 В ящике содержится 7 стандартных и 3 бракованых детали. Детали вынимают последовательно до появления стандартной, не возвращая их обратно. Пусть Х - число извлеченных бракованых деталей. Составить закон распределения этой случайной величины.

7.17 Случайная величина задана функцией плотности распределения f(x). Найти: 1) функцию распределения F(x) и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины в интервал (Построить график функции распределения F(x) и плотности распределения f(x).

Вариант - 18

1.18 Чертежная линейка в поперечном сечении представляет собой равносторонний треугольник. У 2-х таких линеек - красной и зеленой - грани пронумерованы числами 1, 2, 3. Эти линейки бросают на пол, после чего записывают числа, отвечающие их нижним граням. Постройте таблицу, в которую входят все элементарные события для этого эксперимента. пусть k обоэначает номер нижней грани красной линейки, а z - номер нижней зеленой линейки. Найдите: а) р(k=z), б) p(k>z), в) p(k = z).

2.18 На отрезке [0,1] наудачу ставят две точки. Пусть икоординаты этих точек. Рассматриваются следующие события:

А={вторая точка ближе к левому концу отрезка, чем первая точка к правому}; В={корни уравнения х²+2x+действительны}; С={max{} < ½}; D={min{} < ½}. Найти: Р(AВD), Р((АВ)С).

3.18 Из 30 вопросов программы студент знает 25. Билет состоит из 2 вопросов. Опишите: а) пространство элементарных исходов - множество всех билетов; б)событие А - “студент знает два вопроса, содержащиеся в его экзаменационном билете”; в) событие В - “студент знает только один вопрос билета”; г) событие С - “студент не зает ни одного вопроса билета”. Являются ли эти события независимыми и несовместными? Составляют ли они полную систему событий? Найти вероятности событий А, В, С, А+В.

4.18 В трех урнах имеются белые и черные шары. В первой урне - 3 белых и 1 черный шар, во второй - 6 белых и 4 черных шара, в третьей урне - 9 белых и 1 черный шар. Из наугад выбранной урны случайным образом вынимается шар. Найти вероятность того, что он белый. Если извлечен белый шар, то из какой урны он вероятнее всего извлечен?

5.18 а) Вероятность попадания в мишень из винтовки равна 0,004. Сколько стрелков должно стрелять одновременно, чтобы вероятность попадания стала 70%?

б) монету бросают 6 раз. Найти наиболее вероятное число выпадения герба и вероятность появления такого числа гербов;

в) произведено 1000 независимых испытаний с вероятностью наступления интересующего нас события в отдельном испытании равной 0,01. Найти границы, в которых с вероятностью 0,99 заключена частота наступлений события;

г) сколько нужно взять деталей, чтобы наивероятнейшее число годных было равно 25, если вероятность того, что наудачу взятая деталь будет бракованной, равна 0,13. Найти вероятность появления 25 деталей.

6.18 При бросании двух игральных костей игрок выигрывает 25 гр., если на обеих костях выпадает по 6 очков, 3 гр. - если на одной кости выпало 6 очков, 1гр. - если сумма выпавших очков равна 6. Пусть случайная величина Х равна выигрышу, возможному при одном бросании. Составить закон распределения этой случайной величины.

7.18 Случайная величина задана функциейплотности распределения f(x). Найти: 1) функцию распределения F(x) и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины в интервал (Построить график функции распределения F(x) и плотности распределения f(x).

, .

Вариант - 19

1.19. Предположим, что у нас есть брусок, представляющий собой правильную четырехугольную призму, боковые грани которой пронумерованы числами 1, 2, 3, 4, и чертежная линейка, представляющая в поперечном сечении равносторонний треугольник. Грани линейки пронумерованы числами 1, 2, 3. Брусок и линейка катятся по полу, и после остановки отмечаются числа на верхней грани бруска и нижней грани линейки. Постройте пространство элементарных событий и найдите вероятность того, что: а) число на бруске больше числа на линейке; б) эти числа равны; в) сумма этих чисел - простое число.

2.19 На отрезке [0,1] наудачу ставят две точки. Пусть икоординаты этих точек. Рассматриваются следующие события:

А={вторая точка ближе к левому концу отрезка, чем первая точка к правому}; В={корни уравнения х²+2x+действительны}; С={max{} < ½}; D={min{} < ½}.

Найти: Р(AВD), Р((АВ)С).

3.19 Две команды по 10 спортсменов производят жеребьевку для присвоения номеров участникам соревнований.Два брата входят в состав различных команд. Описать: а) пространство элементарных исходов, представляющие пару номеров от 1 до 10; б) событие А- “братья участвуют в соревнованиях под номером 4”; в) событие В- “первый брат участвует в соревнованиях под одним из номеров от 7 до 10 “.Найти вероятности событий А и В.

4.19. Сборщик получил 3 коробки деталей, изготовленных заводом 1, и 2 коробки, изготовленных заводом 2. Вероятность того, что деталь завода 1 стандартна , равна 0,9, а завода 2 - 0,8. Сборщик наудачу извлек деталь из наудачу взятой коробки. Найти вероятность того, что извлечена стандартная деталь. Если извлечена стандартная деталь, то какова вероятность того , что она изготовлена : а) заводом 1 ; б) заводом 2.

5.19. а) среди продукции, изготовленной на данном станке, брак составляет 2% . Сколько изделий необходимо взять ,чтобы с вероятностью 0,995 можно было ожидать , что частота бракованных изделий среди них отличается от 0,02 по абсолютной величине не более чем на 0,005?

б) в урне 10 черных и 5 белых шаров . Испытание заключается в следующем : извлекается шар , фиксируется его цвет , возвращается в урну и тщательно перемешивается. Какова вероятность того , что в 3 испытаниях белый шар появится 1 раз?

в) фабрика выпускает 75% продукции первого сорта .Чему равна вероятность того, что из 300 изделий число первосортных изделий равно 220 ?

г) штамповка металлических клемм для соединительных пластин дает 20% брака .Определить вероятность наличия от 100 до 125 клемм , не соответствующих стандарту партии из 600 клемм.

6.19 В первой урне содержится 3 белых и 5 черных шаров , во второй урне - 6 белых и 4 черных шара , в третьей - 1 белый и 3 черных шара . Из каждой урны вынимают по одному шару. Пусть случайная величина Х - количиство извлеченных черных шаров. Составить закон распределения этой случайной величины.

7.19. Случайная величина задана функцией плотности распределения f(x). Найти: 1) функцию распределения F(x) и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины в интервал (Построить график функции распределения F(x) и плотности распределения f(x).

Вариант - 20

1.20. Выпишите пространство событий, отвечающее обследованию, проводимому для семей, имеющих четырех детей. Чему равна вероятность того, что в семье, имеющей 4-х детей, первые 2 ребенка девочки? Что трое детей мальчики и лишь 1 ребенок девочка? Что в семье имеются 2 мальчика и 2 девочки?

2.20. На отрезке [0,1] наудачу ставят две точки. Пусть икоординаты этих точек. Рассматриваются следующие события:

А={вторая точка ближе к левому концу отрезка, чем первая точка к правому}; В={корни уравнения х²+2x+действительны}; С={max{} < ½}; D={min{} < ½}. Найти: Р(AВC), Р((АВ)D).

3.20. Игральная кость бросается дважды. Найдите: а) вероятности событий АВ, АВ, А\В, если А - “сумма выпавших очков четна”, В - “выпадает хотябы 1 единица”; б) вероятность того, что по крайней мере один раз выпадет меньше 3-х очков. Описать пространство элементарных исходов.

4.20. В каждой из двух урн содержится 2 черных и 8 белых шаров. Из первой урны на удачу извлечен 1 шар и переложен во 2-ю урну, после чего из 2-й урны извлечен шар. Найти вероятность того, что шар, извлеченный из второй урны, окажется белым. Если извлеченный шар оказался белым, то какова вероятность того, что из 1-й урны извлечен и переложен во 2-ю урну: а) белый шар; б) черный шар.

5.20. а) вероятность изготовления детали первого сорта равна 0,9. Найти вероятность того, что из 6 взятых наудачу деталей первого сорта окажется более 4 деталей;

б) в цехе имеется 80 станков, работающих независимо друг от друга. Для каждого станка вероятность того, что в некоторый момент времени включенными окажутся от 60 до 75 станков;

в) вероятность изготовления детали с номинальными размерами равна 0,7. Вычислить вероятность того, что среди 300 деталей номинальными будут 200 деталей;

г) вероятность попадания в цель при каждом выстреле равна 0,001. Найти вероятность попадания в цель двумя и более выстрелами при залпе 3000 орудий.

6.20. При бросании 3 игральных костей игрок выигрывает 18 гр., если на всех костях выпадает 6 очков; 1 гр. 20 коп., если на двух костях выпадает 6 очков; 20 коп., если только на одной кости выпадает 6 очков. Пусть случайная величина Х представляет собой величину выигрыша в гр. Составить закон распределения этой случайной величины.

7.20. Случайная величина задана функцией плотности распределения f(x). Найти: 1) функцию распределения F(x) и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины в интервал (Построить график функции распределения F(x) и плотности распределения f(x).

, .

Вариант - 21

1.21. Два бруска - красный и синий - представляют собой правильные четырехугольные призмы. Боковые грани этих брусков пронумерованы числами 1,2,3 и 4. Бруски покатили по полу и после их остановки заметили числа на верхних гранях брусков. Постройте таблицу для пространства событий, отвечающему этому эксперименту. Если Z - номер верхней грани красного бруска, а Т - номер верхней грани синего бруска, то найдите вероятность того, что: а) сумма чисел на верхних гранях обоих брусков четная; б) Р(большее число равно 4 ); в) Р (Z>T ).

2.21. На отрезке [0,1] наудачу ставят две точки. Пусть икоординаты этих точек. Рассматриваются следующие события:

А={вторая точка ближе к левому концу отрезка, чем первая точка к правому}; В={корни уравнения х²+2x+действительны}; С = { max{} < ½}; D={min{} < ½}.

Найти: Р(AВC), Р((АВ)D).

3.21. Завод в среднем дает 27% продукции высшего сорта и 70% 1-го сорта. Найдите вероятность того, что наудачу взятые 2 изделия из партии в 100 изделий будут: а) высшего сорта; б) 1-го сорта; в) различных сортов. Как изменится вероятность извлечения 2-ч изделий высшего сорта, если известно, что из данной партии перед этим было извлечено 2 изделия высшего сорта. Выразите указанные выше события через события: А - 1-е извлеченное изделие высшего сорта, В - 2-е извлеченное изделие высшего сорта.

4.21. На 3-х станках в одинаковых и независимых условиях изготовляют детали одного наименования. На первомстанке изготовляют 10%, на 2-м - 30%, на 3-м 60% всех деталей. Вероятность каждой детали быть качественной, равна 0,7, если она изготовлена на 1-м станке; 0,8 - если она изготовлена на 2-м станке; 0,9 - если она изготовлена на 3-м станке. Найти вероятность того, что наугад взятая деталь окажется качественной. Если наугад взятая деталь оказалась качественной, то на каком станке она вероятнее всего изготовлена?

5.21. а) В цехе имеется 80 станков, работающих независимо друг от друга. Для каждого станка вероятность быть включенным равна 0,9. Найти вероятность того, что в некоторый момент времени включенными окажется наиболее вероятное число станков. Чему равно это число?

б) вероятность попадания в цель из револьвера равна 0,66. Проведено 200 выстрелов по цели. Чему равна вероятность того, что число попаданий в цель заключено между 120 и 150?

в) при изготовлении радиоламп в среднем бывает 2% брака. Найти вероятность того, что в партии из 200 ламп не более бракованных; г) всхожесть семян некоторого растения составляет 80%. Какова вероятность того, что из 10 посеянных семян взойдут: 9; по крайней мере 8; не менее 9.

6.21. В группе из 5-и изделий имеется 1 бракованное. Чтобы его обнаружить, наугад берут одно изделие за другим и проверяют. Построить ряд распределений случайной величины Х, представляющей собой количество извлеченных деталей до обнаружения бракованной.

7.21. Случайная величина задана функцией плотности распределения f(x). Найти: 1) функцию распределения F(x) и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины в интервал (Построить график функции распределения F(x) и плотности распределения f(x).

, .

Вариант - 22

1.22. Из букв слова “мост” наугад одну за другой выбирают 2. Выпишите пространство элементарных событий для этого эксперимента. Чему равна вероятность того, что: а) в выбранной паре букв нет гласной? б) в выбранной паре букв гласная на втором месте?

2.22. На отрезке [0,1] наудачу ставят две точки. Пусть икоординаты этих точек. Рассматриваются следующие события:

А={вторая точка ближе к левому концу отрезка, чем первая точка к правому}; В={корни уравнения х²+2x+действительны}; С={max{} < ½}; D={min{} < ½}. Найти: Р(AВC), Р((АВ)D).

3.22. Среди 17 студентов группы, из которых 8 девушек, разыгрывается 7 билетов. Причем, каждый может выиграть только 1 билет. Описать: а) пространство элементарных исходов; б) событие А - “среди обладателей билетов окажется 4 девушки”; в) событие В - “среди обладателей билетов только девушки”; г) событие С - “среди обладателей билетов только юноши”. Вычислите вероятность событий А, В, С. Являются ли события А, В, С попарно независимыми и попарно несовместными?

4.22. Имеется 5 винтовок, из которых 2 с оптическим прицелом. Вероятность попадания в цель при выстреле из винтовки с оптическим прицелом составляет для данного стрелка 0,95; без оптического прицела - 0,8. Найти вероятность попадания в цель, если стрелок сделает 1 выстрел из наудачу взятой винтовки.

5.22. а) вероятность изготовления детали высшего сорта на данном станке равна 0,45. Найти вероятность того, что среди взятых наудачу 280 деталей половина окажется высшего сорта;

б) пусть вероятность того, что телевизор потребует ремонта в течение гарантийного срока, равна 0,1. Найти вероятность того, что в течение гарантийного срока из 5 телевизоров: не более 2 потребует ремонта; хотя бы 2 потребует ремонта;

в) вероятность изготовления деталей с номинальными размерами равна 0,7. Вычислить вероятность того, что среди 300 деталей номинальными будут от 200 до 250;

г) аппаратура содержит 2000 одинаково надежных элементов, вероятность отказа для каждого из которых равна 0,0005. Какова вероятность отказа аппаратуры, если она наступает при отказе хотя бы одного из элементов?

6.22. На карточках запнсаны двузначные числа от 31 до 60. Карточку извлекают из урны, фиксируют, возвращают в урну.

7.22. Случайная величина задана функцией плотности распределения f(x). Найти: 1) функцию распределения F(x) и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины в интервал (Построить график функции распределения F(x) и плотности распределения f(x).

, .

Вариант - 23

1.23. Игральная кость бросается дважды. Опишите пространство элементарных событий этого эксперимента, если его элементами служат суммы выпавших очков. Введите элементарные вероятности, считая равновозможными выпадение любой пары очков. Найдите вероятности событий: А - “сумма очков больше 9 “; В - “сумма очков делится на 3 “.

2.23. На отрезке [0,1] наудачу ставят две точки. Пусть икоординаты этих точек. Рассматриваются следующие события:

А={вторая точка ближе к левому концу отрезка, чем первая точка к правому}; В={корни уравнения х²+2x+действительны}; С={max{} < ½}; D={min{} < ½}. Найти: Р((AВ)ВС)), Р(А).

3.23. Наудачу взятый телефонный номер состоит из 5 цифр. Опишите: а) пространство элементарных исходов, представляющее множество пятизначных телефонных номеров; б) событие А - “телефонный номер состоит из различных цифр”; в) событие В - “ телефонный номер состоит из четных цифр”; г) событие С - “телефонный номер состоит из нечетных цифр”; д) событие D - “телефонный номер делится на 4 “. Вычислите вероятности событий А, В, С, D. Являются ли эти события попарно несовместными и попарно независимыми?

4.23. 2 перфораторщицы набили по одинаковому комплекту перфокарт. Вероятность того, что 1-я перфораторщица допустит ошибку, равна 0,05; для 2-й перфораторщицы эта вероятность равна 0,1. Какова вероятность того, что в наудачу взятом комплекте перфокарт будет найдена ошибка? Какова вероятность того, что эту ошибку допустит: а) 1-я перфораторщица; б) 2-я перфораторщица?

5.23. а) при контроле из партии в 1000 деталей выбрали 50 штук. Найти вероятность того, что в выборке не окажется дефектных изделий, если во всей партии содержится 4 дефектных изделия;

б) пусть вероятность того, что покупателю необходима обувь 41-го размера, равна 0,3. Найти вероятность того, что из 5 первых покупателей обуви этого размера будер необходима: одному; по крайней мере одному;

в) из большой партии продукции, содержащей 70% изделий первого сорта, наугад отбирают 100 изделий. Вычислить вероятность того, что среди отобраных будет не менее и не более 90 изделий первого сорта;

г) автоматическаяштамповка клемм для предохранителей дает 10% отклонений от принятого стандарта. сколько стандартных клемм следует ожидать с вероятностью 0,2420 среди 400 клемм?

6.23. По мишени ведутся выстрелы до 1-го попадания или до израсходования всех патронов. Составить закон распределения случайной величины Х - числа израсходованных патронов, если вероятность попадания при каждом выстреле равна 0,6.

7.23. Случайная величина задана функцией плотности распределения f(x). Найти: 1) функцию распределения F(x) и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины в интервал (Построить график функции распределения F(x) и плотности распределения f(x).

, .

Вариант - 24

1.24. Числа 1, 2, 3 и 4 пишутся на 4-х листах бумаги. после этого листки кладутся в шляпу и перемешиваются. Человек с завязанными глазами вынимает один за другим 2 листка. Описать пространство элементарных событий отвечающих этому эксперименту. Если х - номер на первом листе, у - номер на втором листе, то найдите: а) р(х>y); б) вероятность того, что сумма чисел на обоих листах четная; в) вероятность того, что сумма чисел на этих листах - простое число.

2.24. На отрезке [0,1] наудачу ставят две точки. Пусть икоординаты этих точек. Рассматриваются следующие события:

А={вторая точка ближе к левому концу отрезка, чем первая точка к правому}; В={корни уравнения х²+2x+действительны}; С={max{} < ½}; D={min{} < ½}. Найти: Р((AВ)ВС)), Р(В).

3.24. 12 различных книг расставляются наудачу на одной полке. Опишите: а)пространство элементарных исходов; б) событие А - “ 3 определееные книги оказались поставленные рядом “; в) событие В - “ 3 определенные книги стоят на 5-м, 6-м и 7-м месте”. Определите вероятности событий А и В. Являются ли события А и В независимыми и несовместимыми?

4.24. Имеется 3 урны, в каждой из которых 7 белых и 13 черных шаров. Из первой во вторую перекладывается 1 шар; затем из второй в третью - 1 шар. Найти вероятность того, что из второй урны в третью был переложен: а) белый шар; б) черный шар.

5.24. а) вероятность того, что деталь нестандартна, равна 0,04. Найти, сколько деталей нужно отобрать, чтобы с вероятностью равной 0,9964, можно было утверждать, относительная частота появления нестандартных деталей (среди отобранных) относится от постоянной вероятности р=0,04 по абсолютной величине не более, чем на 0,01;

б) в цехе 4 мотора. Для каждого мотора вероятность того, что он включен, равна 0,6. Найти вероятность того, что в данный момент: включено 2 мотора; включены все моторы;

в) вероятность того, что любой абонент позвонит на коммутатор в течение часа равна 0,01. Телефонная станция обслуживает 300 абонентов. Какова вероятность того, что в течение часа позвонят 4 абонента?

г) предприятие имеет 2400 агрегатов. В каждый агрегат входит некоторая деталь, вероятность выхода, из строя которой за время t равна 1/6. Исходя из этого, отдел снабжения приготовил на время t 400 запасных деталей этого типа. Найти вероятность того, что это количество запасных деталей обеспечит бесперебойную работув течение времени t.

6.24. В партии, состоящей из 10 деталей, имеется 4 бракованных. Наугад извлекают 3 детали. Составить закон распределения случайной величины Х, представляющей собой количуство бракованных деталей среди 3-х выбранных.

7.24. Случайная величина задана функцией плотности распределения f(x). Найти: 1) функцию распределения F(x) и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины в интервал (Построить график функции распределения F(x) и плотности распределения f(x).

, .

Вариант - 25

1.25. В урне имеется 6 шаров с номерами от 1 до 6. Наудачу извлекают по 1 3 шара. Найдите вероятность того, что: 1) числа 1, 2, 3 появятся последовательно в порядке извлечения; 2) появятся шары с номерами 1, 2, 3 в любом порядке, если шары извлекаются: а) с возвращением; б) без возвращения.

2.25. На отрезке [0,1] наудачу ставят две точки. Пусть икоординаты этих точек. Рассматриваются следующие события:

А={вторая точка ближе к левому концу отрезка, чем первая точка к правому}; В={корни уравнения х²+2x+действительны}; С={max{} < ½}; D={min{} < ½}. Найти: Р((AВ)ВС)), Р(С).

3.25. Для уменьшения общего количества игр на соревнованиях 20 валейбольных команд разбиты по жребию на 4 подгруппы (по 5 в каждой). Среди команд имеется 4 наиболее сильные. Опишите: а) пространство элементарных исходов, получаемое при разбиении команд на 4 подгруппы; б) событие А - “4 наиболее сильные команды оказались в разных подгруппах”; в) событие В - “4 наиболее сильные команды оказались в одной подгруппе”; г) событие С - “2 наиболее сильные команды попали в 1-ю подгруппу”. Определите вероятности событий А, В, С. Совместна ли эти события.

4.25. С первого станка на сборку поступает 40%, со второго 30%, с третьего 20%, счетвертого 10% всех деталей. Среди деталей первого станка 0,1% бракованных, второго - 0,2%, третьего 0,25%, четвертого 0,5%. Найти вероятность того, что поступившая на сборку деталь бракованная. Если поступившая на сборку деталь оказалась бракованной, то каким станком вероятнее всего она была изготовлена.

5.25. а) На автобазе имеется 10 автомашин. Вероятность выхода на линию каждой из них 0,8. Найти вероятность нормальной работы автобаза в ближайший день, если для этого необходимо иметь на линии не менее 8 машин;

б) по данным ОТК в среднем 3% изделий требует дополнительной регулировки. Вычислить вероятность того, что из 200 изделий 4 потребуют дополнительной регулировки;

в) определить вероятность того, что среди 400 поб руды окажется 275 проб с помышленным содержанием металла, если вероятность промышленного содержания металла одинаково для каждой пробы и равна 0,7;

г) массовый выпуск болтов дает в среднем 2% брака. Определить вероятность того, что в партии из 1000 болтов отклонение от этой доли брака будет меньше чем 0,01.

6.25. Вероятность того, что трамвай подойдет к остановке строго по расписанию, равна 0,7. Составить закон распределения случайной величины Х, представляющей собой количество бракованных деталей среди 3-х выбранных.

7.25. Случайная величина задана функцией плотности распределения f(x). Найти: 1) функцию распределения F(x) и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины в интервал (Построить график функции распределения F(x) и плотности распределения f(x).

, .

Вариант - 26

1.26. За круглым столом случайным образом рассаживаются 7 человек. Среди них есть 2 подруги. Какова вероятность того, что: а) они окажутся рядом; б) между ними будет один человек.

2.26. На отрезке наудачу ставят две точки. Пусть икоординаты этих точек. Рассматриваются следующие события:

А={вторая точка ближе к левому концу отрезка, чем первая точка к правому}; В={корни уравнения х²+2x+действительны}; С={max{} < ½}; D={min{} < ½}. Найти: Р((AВ)ВС)), Р(D).

3.26. На 100 карточках написаны числа от 1 до 100. Опишите: а) пространство элементарных исходов; б) событие А - “карточка содержит цифру 0”; в) событие В - “карточка содержит цифру 5 “. Найдите вероятности событий А и В. Являются ли события А и В совместными и зависимыми.

4.26. В 2-х урнах находится, соответственно, 5 и 15 черных и 20 и 5 белых шаров. Из каждой урны на удачу извлекают 1 шар, а затем из этих 2-х шаров наудачу берется 1. Какова вероятность, что это шар черный? Если извлеченный шар оказался черным, то какова вероятность того, что: а) из обеих урн были извлечены черные шары; б) из 1-й извлечен белый шар, из 2-й - черный; в) из 1-й извлечен черный шар, из 2-й - белый.

5.26. а) монету бросают 5 раз. Найти вероятность того, что герб выпадает не менее 4 раз;

б) среди семян ржи 0,4% семян сорников. Какова вероятность при случайном отборе 500 семян обнаружить 5 семян сорняков;

в) производится стрельба по цели. Вероятность попадания при одном выстреле Т=0,3. Производится 100 выстрелов. Какова вероятность того, что цель поражена в большинстве выстрелов?

г) сколько нужно взять деталей, чтобы наивероятнейшее число годных было равно 50, если вероятность того, что наудачу взятая деталь будет бракованной, равна 0,1? Какова вероятность появления 50 годных деталей в указанной партии?

6.26. В лотерее разыгрывается мяч стоимостью 3 гр., шахматы стоимостью 10 гр. и кеды стоимостью 5 гр. Всего билетов 10. Пусть случайная величина Х представляет собой величину выигрыша в гривнях для лица, имеющего 3 билета. Составить закон распределения этой случайной величины.

7.26. Случайная величина задана функцией плотности распределения f(x). Найти: 1) функцию распределения F(x) и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины в интервал (Построить график функции распределения F(x) и плотности распределения f(x).

Индивидуальное задание № 1

Вариант №___

Индивидуальное задание №2

Обозначения: – номер группы. Например, для групп МТ-291, МТ-292, МТ-191, МТ-192, соответствующие номера групп будут равны 21, 22, 11, 12. То есть, вторая цифра - год поступления - опускается. Через обозначается номер студента в списке группы.

Все данные приведены в брошюре В.Ф. Пожидаев «Прикладные задачи математической статистики», Луганск, издательство ВУГУ, 1998.

1. Дискретная случайная величина принимает два значения: и с вероятностями .и (). При этом . По условию задачи даны числовые значения , , и . Требуется найти значения и . Для каждого варианта значения и 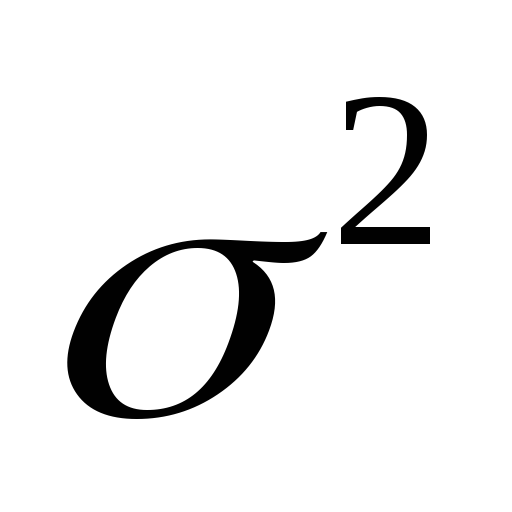определяются выражениями:

, , .

2. В рамках предыдущей задачи даны 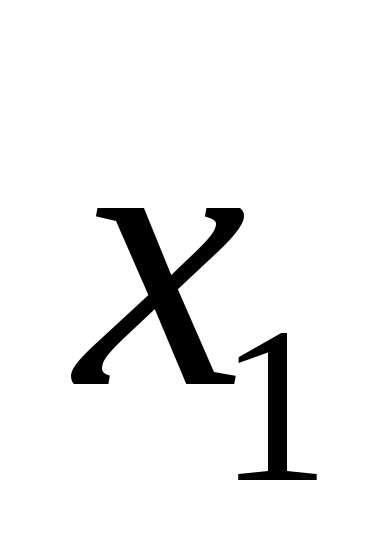, и . Требуется найти и . При этом для каждого варианта исходные данные задаются формулами:

, , .

3. Случайная величина равномерно распределена в интервале , границы которого неизвестны. Найти эти границы, если математическое ожидание и дисперсия заданы. При этом для каждого варианта:

, .

4. По двум значениям функции распределения и в точках и нормально распределенной случайной величины требуется найти ее математическое ожидание и дисперсию. При этом для каждого варианта:

, , , .

5. Треугольное распределение (распределение Симпсона) задано на отрезке 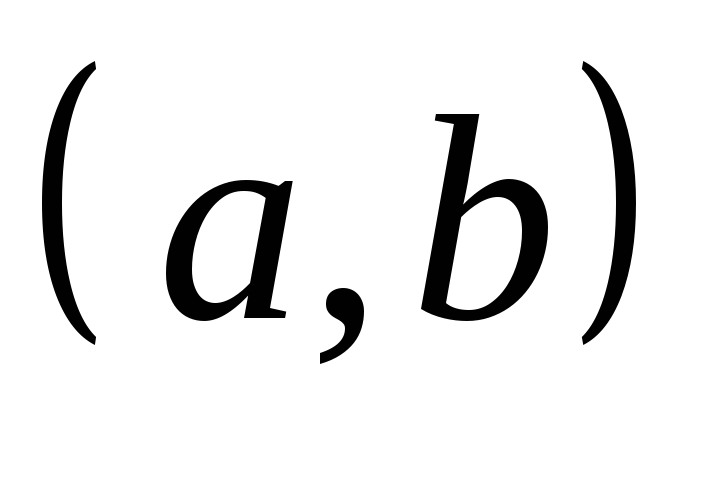. Найти математическое ожидание , дисперсию , асимметрию и эксцесс , если границы интервала для каждого варианта равны:

, .

6. Случайная величина подчиняется логарифмически нормальному закону с параметрами и , задаваемыми по правилам: , 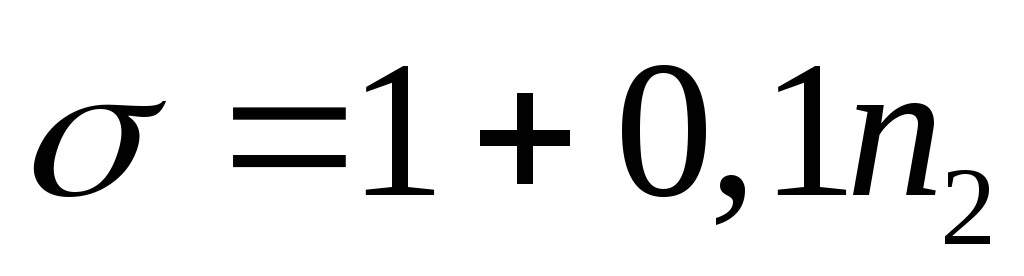. Найти математическое ожидание и вероятность попадания в интервал , границы которого задаются равенствами: , .

7. Вероятность того, что каждый из 30000 исследованных образцов минерала обладает признаком А, равна 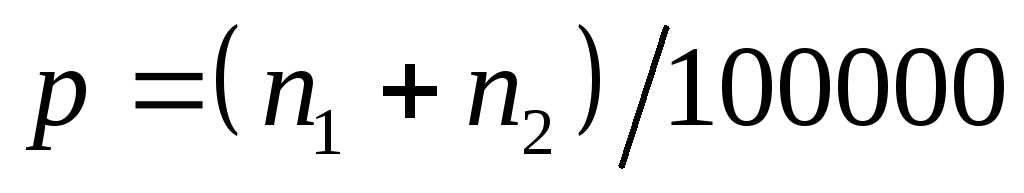. Найти границу отклонения частоты появления признака А от его вероятности по абсолютной величине, если это отклонение можно ожидать с вероятностью, не меньшей , причем .

8. Случайная величина описывается законом Релея , . Дано: .

Найти: математическое ожидание , дисперсию , асимметрию и эксцесс

9. Закон распределения случайной величины  экспоненциальный , .

Дано: . Найти: математическое ожидание , дисперсию , третий и четвертый центральный моменты, асимметрию и эксцесс .

10. Случайная величина распределена по закону Вейбула 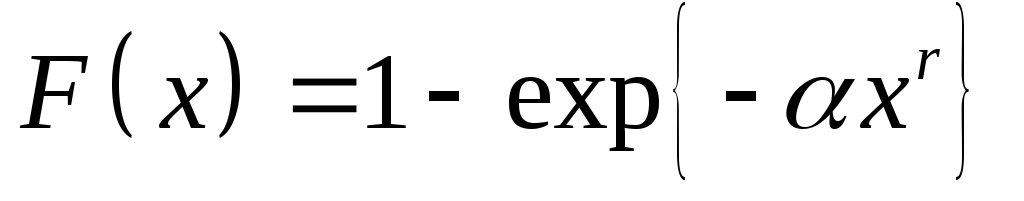. По заданным значениям 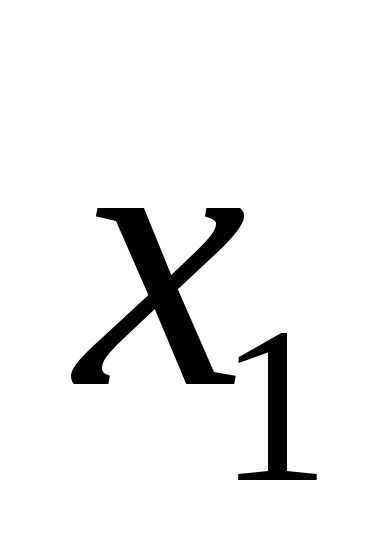, и , требуется найти параметры и закона распределения, а также вычислить математическое ожидание .

, ; , .

11. Случайная величина описывается законом Эрланга

.

Дано: , , , .

Найти: математическое ожидание и вероятность .

12. В законе распределения Парето при и при по условию заданы:

, , и .

Найти: константу , математическое ожидание , дисперсию и вероятность попадания случайной величины в интервал .

13. Случайная величина равномерно распределена на отрезке (-1,+1). Построить закон распределения случайной величины , при и при . Найти ее математическое ожидание , дисперсию , третий и четвертый центральный моменты, асимметрию и эксцесс .

14. Случайный вектор задан распределением:

где . Вектор задан своими компонентами: , . Найти матрицу ковариации вектора . Будут ли случайные величины и независимыми?

Индивидуальное задание №2

Вариант №___

Указания к решению индивидуальных заданий

по теме «Теория вероятностей и математическая статистика»

1. Построить вариационный ряд (расположить все числа в порядке возрастания). Произвести проверку на критерий резко выделяющихся наблюдений (брошюра В.Ф. Пожидаев «Прикладные задачи математической статистики», Луганск, издательство ВУГУ, 1998). Если критерий выполняется, то откинуть резко выделяющиеся значения.

2. Найти количество интервалов, на которые будет разбиваться выборка, по формуле , где – обьем выборки.

3. Найти верхнюю и нижнюю границы вариационного ряда: 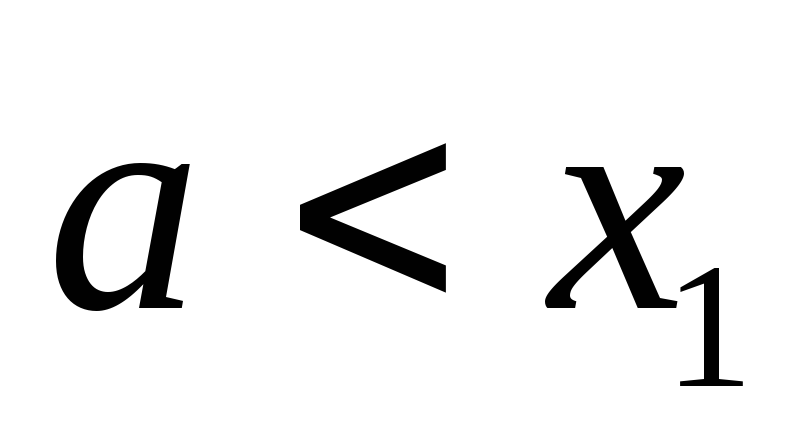и .

4. Разбить интервал 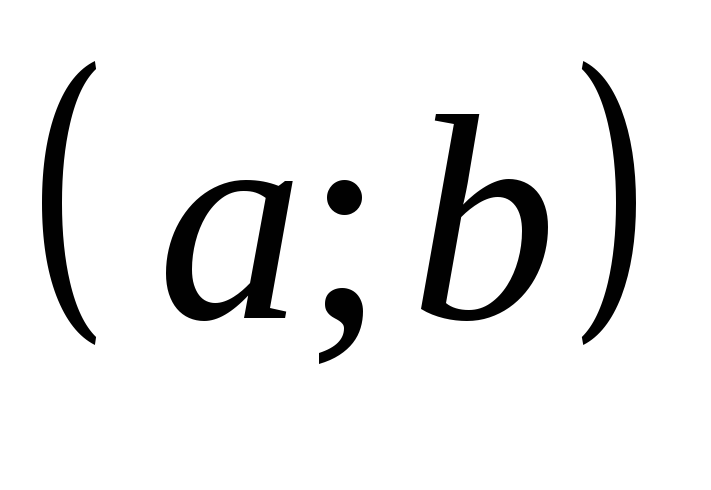на отрезков, длиной .

5. По сгруппированным данным найти – число попаданий элементов выборки в каждый из выделенных интервалов. Оценить вероятность попадания в каждый из интервалов .

6. Построить гистограмму распределения, эмпирическую функцию распределения (, ).

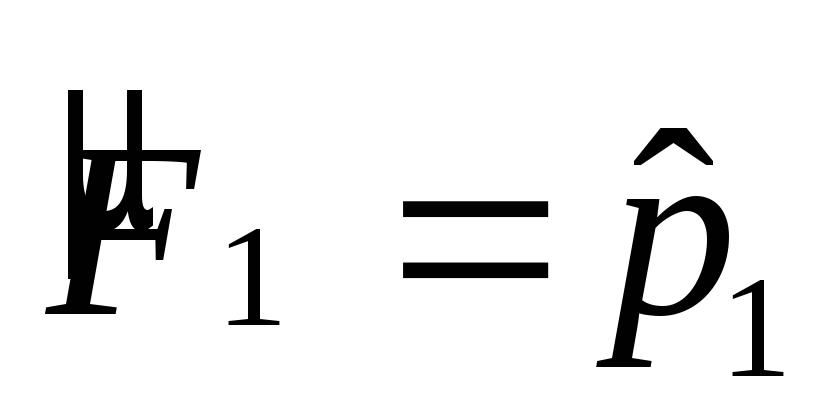7. Найти математическое ожидание (), дисперсию (), третий и четвертый центральные моменты (), ассиметрию (), эксцесс () по исходной выборке и по сгруппированным данным.

8. К сгруппированным данным применить поправки Шеппарда: , , 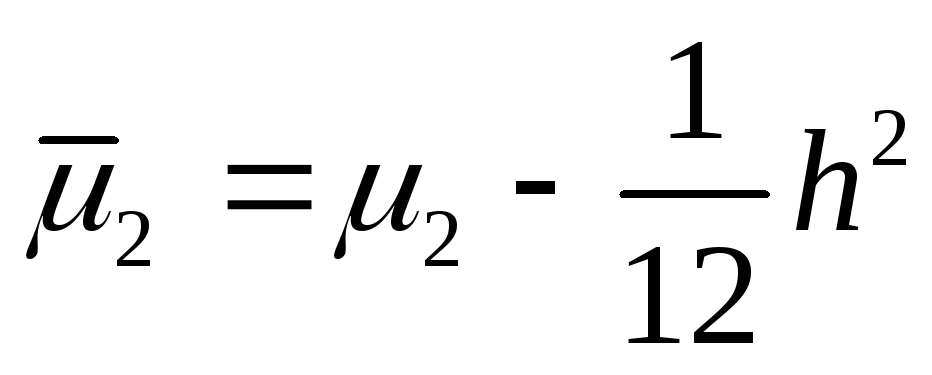, (в качестве дополнительного задания доказать используемые формулы с помощью поправок Шеппарда для начальных моментов).

9. Для задания №4 предположить наиболее похожие законы распределения (не более 3 законов, графически – пункт 6 – использовать брошюру: В.Ф. Пожидаев «Прикладные задачи математической статистики», Луганск, издательство ВУГУ, 1998).

10. Выбрать способ оценки параметров распределения: метод максимального правдоподобия, метод вероятностной бумаги, метод моментов. Выполнить оценку параметров распределения.

11. Выполнить проверку гипотезы об адекватности пердположения, выдвинутого в пункте №9. Для этого использовать критерий – Пирсона, или – критерий Колмогорова.

Решение типового варианта

24.343 24.179 19.176 7.416 26.681 56.841 6.622 30.650 27.491 2.337

25.707 5.071 32.370 38.044 12.440 32.620 31.625 19.707 16.095 39.679

24.086 22.074 44.012 31.639 61.291 39.538 56.279 44.664 68.745 37.706

29.007 20.375 39.035 20.026 68.824 28.094 14.568 17.593 23.988 29.985

14.340 22.972 41.521 10.300 37.704 18.526 58.808 11.819 6.009 27.037

26.472 58.306 7.660 12.020 41.053 28.400 16.006 9.913 19.777 39.995

31.360 24.583 33.951 6.878 37.849 50.063 29.861 26.806 16.379 5.002

28.100 16.708 27.716 44.131 30.454 18.224 44.105 10.532 53.107 40.943

39.201 11.958 45.166 24.062 11.090 6.600 27.541 12.106 15.074 2.741

24.784 18.490 29.826 26.012 38.177 47.171 39.671 45.972 28.202 52.287

1). Для построения вариационного ряда отсортируем исходный ряд в порядке неубывания. Получим таблицу группировки частот:

2.337	9.913	14.568	19.176	24.179	27.491	29.985	37.706	40.943	50.063
2.741	10.300	15.074	19.707	24.343	27.541	30.454	37.849	41.053	52.287
5.002	10.532	16.006	19.777	24.583	27.716	30.650	38.044	41.521	53.107
5.071	11.090	16.095	20.026	24.784	28.094	31.360	38.177	44.012	56.279
6.009	11.819	16.379	20.375	25.707	28.100	31.625	39.035	44.105	56.841
6.600	11.958	16.708	22.074	26.012	28.202	31.639	39.201	44.131	58.306
6.622	12.020	17.593	22.972	26.472	28.400	32.370	39.538	44.664	58.808
6.878	12.106	18.224	23.988	26.681	29.007	32.620	39.671	45.166	61.291
7.416	12.440	18.490	24.062	26.806	29.826	33.951	39.679	45.972	68.745
7.660	14.340	18.526	24.086	27.037	29.861	37.704	39.995	47.171	68.824

2). Количество интервалов разбиения определяется формулой:

3). Выберем границы интервала, в котором лежит эта выборка: ,. Необходимое неравенство выполняется:

.

4). Высчитываем шаг интервала, как , где - это наименьшее значение элемента в таблице группировки частот, а - наибольшее. В нашем случае

5), 6). Найдем число попаданий элементов выборки в каждый из этих интервалов. Оценим вероятность попадания в каждый из определенных интервалов и все полученные данные занесем в таблицу. Также в таблицу добавим столбец , в котором укажем середину - го интервала.

№ инт.	Интервал
1		11	0,11	0,11	5
2		22	0,22	0,33	15
3		28	0,28	0,61	25
4		19	0,19	0,8	35
5		10	0,1	0,9	45
6		10	0,1	1	60

Пояснение: – абсолютная частота, – относительная частота, - относительная частота, – середина интервала. Гистограмма строится по данным столбца .

2). Пользуясь таблицей, строим гистограмму абсолютных частот:

По внешнему виду гистограммы распределения делаем предположение, что имеет место распределение Релея.

Эмпирической функцией распределения (функцией распределения выборки) называют функцию , определяющую для каждого значения х относительную частоту события :

,

где - число вариант, меньших ; - объем выборки.

Эмпирическая функция обладает следующими свойствами:

Свойство 1. Значения эмпирической функции принадлежат отрезку [0;1];

Свойство 2. - неубывающая функция;

Свойство 3. Если - наименьшая варианта, а - наибольшая, то при и при .

Исходя из данных нашей выборки, а после произведенных расчетов, данных таблицы столбца мы можем записать искомую эмпирическую функцию и построить ее график.

8). Оценка параметров по исходной выборке: - математическое ожидание, - дисперсия, - третий центральный момент, - четвертый центральный момент, - асимметрия, - эксцесс.

Произведем по этим формулам вычисления для наших данных:

28,32	233,59	1746,78	149679,22	0,49	-0,262

9).Оценка параметров по сгруппированным данным: - математическое ожидание, - дисперсия, - третий центральный момент, - четвертый центральный момент, - асимметрия, - эксцесс.

Произведем по этим формулам вычисления для наших данных:

27,8	228,16	1761,5	140677,04	0,51	-0,3

10). Будем пользоваться следующими формулами поправок Шеппарда для начальных моментов:

В нашем случае имеем:

,

После применения поправок значения еще больше отдалились от значений параметров по исходной выборке. Это значит, что внутри интервалов распределение далеко от равномерного. Следовательно, к этому распределению нельзя применить ступенчатую аппроксимацию.

11). Существует несколько способов оценки параметров распределения. Рассмотрим некоторые из них.