IV. УСТАНОВИВШИЙСЯ ПРИТОК ЖИДКОСТИ К ГРУППЕ СОВЕРШЕННЫХ СКВАЖИН

1. Интерференция скважин. Принцип (метод) суперпозиции

Обычно месторождение эксплуатируется десятками и сотнями скважин. Все скважины в процессе работы взаимодействуют (интерферируют) между собой, т.е. под влиянием остановки, пуска или изменения режима работы одной группы скважин изменяются дебиты и забойные давления другой группы скважин, эксплуатирующих тот же пласт. Интерференция скважин является одной из сложных задач подземной гидрогазодинамики, представляющих несомненный интерес для теории и практики разработки нефтяных и газовых месторождений. Прежде чем перейти к исследованию задач интерференции скважин, введем некоторые необходимые понятия.

Назовем точечным стоком на плоскости точку, поглощающую жидкость. Сток можно рассматривать как гидродинамически совершенную скважину бесконечно-малого радиуса в пласте единичной толщины. На плоскости вокруг точечного стока будет радиальное движение. Точечный источник – это точка, выделяющая жидкость (модель нагнетательной скважины).

Найдем потенциал Ф точечного стока на плоскости. Поскольку точечный сток является моделью добывающей скважины и течение вокруг него плоско-радиальное, то можно воспользоваться формулой скорости фильтрации для потока этого типа (3.26)

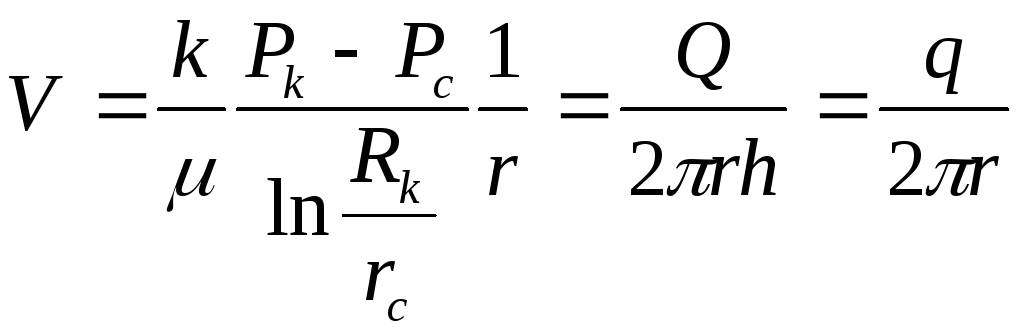, (4.1)

где - дебит скважины-стока, приходящийся на единицу толщины пласта.

Но для плоско-радиального потока

,

откуда .

После интегрирования получим выражение потенциала Ф для точечного стока на плоскости

, (4.2)

где С – постоянная интегрирования, которая легко находится по граничным условиям . При поэтому в этих точках потенциал Ф теряет смысл.

Для точечного источника формула (4.2) остается в силе, но q считается отрицательным (q<0).

Из формулы (4.2) следует, что линиями равного потенциала (эквипотенциалями) являются окружности r=const.

Найдем теперь выражение потенциала точечного стока в пространстве. Движение вблизи такого стока будет радиально-сферическим. Поэтому скорость фильтрации

откуда После интегрирования получаем

. (4.3)

Формула (4.3) – потенциал точечного стока в пространстве.

Как видно из (4.3), при а при

Модель точечного стока в пространстве будет использоваться при решении задач притока жидкости к гидродинамически несовершенным скважинам.

На основе свойств уравнения Лапласа, которым описывается распределение давления P(r) и потенциала Ф(r) в установившихся потоках жидкости в пласте, в подземной гидрозазодинамике разработан метод решения сложных гидродинамических задач, названный методом суперпозиции (методом наложения).

Математический смысл метода суперпозиции заключается в том, что если имеется несколько фильтрационных потоков с потенциалами Ф₁(x,y,z), Ф₂(x,y,z), …, Ф_n (x,y,z), каждый из которых удовлетворяет уравнению Лапласа, т.е.

, j=1,2,3…n,

то сумма

, где C_j-произвольная постоянная

также удовлетворяет уравнению Лапласа.

Гидродинамический смысл метода суперпозиции – изменения давления или потенциала в любой точке пласта, вызванные работой каждой скважины (добывающей или нагнетающей),алгебраически суммируются в каждой точке пласта. При этом суммарная скорость фильтрации находится как сумма векторов скоростей фильтрации, вызванных работой каждой скважины в отдельности.

Пусть на неограниченной плоскости расположено n источников и стоков (рис.19). Потенциал каждого из них в некоторой точке М определяется по формуле (4.2):

г де r₁, r₂, r₃, ..r_n – расстояния от соответствующих стоков до точки М; С₁, С₂, С₃,…, С_n – постоянные.

Рис. 19

Каждая функция Ф₁, Ф₂, … Ф_n удовлетворяет уравнению Лапласа. Поэтому сумма потенциалов

где С=С₁+С₂+…+С_n (4.4)

также удовлетворяет уравнению Лапласса.

Физически это означает, что фильтрационные потоки от работы каждого источника или стока накладываются друг на друга.

Вектор скорости фильтрации в точке М будет определяться векторной суммой:

(4.5)

где

Метод суперпозиции можно использовать не только в бесконечных пластах, но и в пластах, имеющих контур питания или непроницаемую границу той или иной формы. В этом случае для выполнения тех или иных условий на границах приходится вводить фиктивные скважины – стоки или скважины-источники за пределами пласта. Фиктивные скважины в совокупности с реальными скважинами обеспечивают необходимые условия на границах. При этом задача сводится к рассмотрению одновременной работы реальных и фиктивных скважин в неограниченном пласте. Этот метод называется методом отображения источников и стоков.

Ниже рассматриваются решения некоторых задач с применением метода суперпозиции совместно с методом отображения источников и стоков, имеющих практическое применение в теории разработки нефтяных и газовых месторождений.

2. Приток жидкости к группе скважин в пласте

с удаленным контуром питания

Пусть в горизонтальном пласте толщиной h расположена группа скважин А₁, А₂, … ,А_n радиусами r_cj, работающих с различными забойными потенциалами Ф_cj (j=1,2,3,…,n) (рис.20). Расстояния между центрами скважин известны (r_ji=r_ij).

Так как контур питания находится далеко от всех скважин, то можно приближенно считать, что расстояние от всех скважин до всех точек контура питания одно и тоже и равно R_к . Потенциал на контуре питания Ф_к задан. Требуется определить дебит каждой скважины и скорость фильтрации в любой точке пласта.

Рис. 20

Потенциал в любой точке пласта М определяется по формуле (4.4). Поместив мысленно точку М последовательно на забой каждой скважины, получим выражения для забойного потенциала на них

(4.5)

В выражениях (4.5) принято, что расстояние от точки на стенке данной скважины i до центра любой другой скважины j равно расстоянию между центрами этих скважин, так как r_ci<<r_ij (i не равно j). Система (4.5) состоит из n уравнений и содержит n+1 неизвестных (n дебитов q и одну const=C). Дополнительное уравнение получим, поместив точку М на контур питания:

. (4.6)

Вычитая почленно каждые из уравнений (4.5) из (4.6), исключим постояннуюС и получим систему из n уравнений, решив которую можно определить дебиты скважин q₁, q₂, q₃, … q_n, если заданы забойные Ф_с1, Ф_с2, Ф_с3, …, Ф_сn и контурный Ф_к потенциалы. Имеем:

(4.7)

Точно также решается из системы уравнений (4.7) и обратная задача – это определение потенциалов по известным дебитам q_j (j=1,2,3,…,n).

Скорость фильтрации V в любой точке пласта определяется как геометрическая сумма скоростей фильтрации, вызванных работой каждой скважины

. (4.8)

направлена по радиусу от точки М к данной скважине-стоку.