
-
Теорія визначників n-го порядку.
Для введення поняття визначника
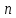 -го
порядку потрібна інформація з теорії
перестановок і підстановок.
-го
порядку потрібна інформація з теорії
перестановок і підстановок.
-
Перестановки з n символів.
Означення 1. Перестановкою
з
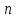 символів називається розташування цих
символів в деякому порядку.
символів називається розташування цих
символів в деякому порядку.
Означення 2. Транспозицією називається таке перетворення перестановки, при якому два її елементи міняються місцями.
Теорема
1. З
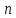 символів можна скласти
символів можна скласти
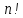 перестановок.
перестановок.
Доведення.
Застосуємо метод математичної індукції по кількості символів n.
-
При
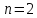 це твердження є правильним,
бо маємо дві перестановки: 1 2, 2 1.
це твердження є правильним,
бо маємо дві перестановки: 1 2, 2 1. -
Зробимо індуктивне припущення: з
 символів можна скласти
символів можна скласти
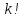 перестановок.
перестановок. -
Покажемо справедливість індуктивного переходу для
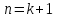 .
.
Розглянемо
всі перестановки з
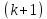 символів за такою схемою.
Запишемо спочатку всі перестановки, що
починаються з одних одиниць.
символів за такою схемою.
Запишемо спочатку всі перестановки, що
починаються з одних одиниць.
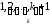
Ця
група знаходиться в умовах індуктивного
припущення. За індуктивним припущенням
з
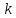 символів утворюється
символів утворюється
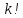 перестановок.
перестановок.
Запишемо всі перестановки, що починаються з двійки, трійки, тощо.
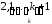
Останньою
буде група перестановок, що починаються
з
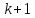 .
.
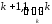
Таким
чином всі перестановки розбиваються
на k+1 клас, в кожний з яких входить k
перестановок. Отже всього буде
k!(k+1)=1ˑ2ˑ…ˑkˑ(k+1)=(k+1)!
перестановок.
З доведеного за принципом математичної
індукції дане твердження є правильним
при довільному натуральному
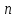 .
.
Теорема 2. Усі
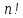 перестановок з
перестановок з
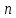 символів можна записати таким списком,
в якому кожна наступна перестановка
може бути отримана з попередньої шляхом
однієї транспозиції.
символів можна записати таким списком,
в якому кожна наступна перестановка
може бути отримана з попередньої шляхом
однієї транспозиції.
Доведення
Застосуємо метод математичної індукції по кількості символів n.
При
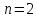 це очевидно: 1,2;
це очевидно: 1,2;
2,1.
Зробимо
індуктивне припущення: вважатимемо
правильним дане твердження при
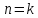 .
Доведемо справедливість твердження
при
.
Доведемо справедливість твердження
при
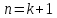 .
Запишемо всі перестановки, що починаються
з 1.
.
Запишемо всі перестановки, що починаються
з 1.
1,
2,
3, ...
,
 ,
,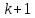
1, ...
Розглянувши
останні
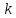 символів бачимо, що для цих
перестановок діє індуктивне припущення.
Тоді ці перестановки можна записати
потрібним списком. Аналогічні міркування
застосуємо для тих перестановок, що
починаються з 2, 3, ...,
символів бачимо, що для цих
перестановок діє індуктивне припущення.
Тоді ці перестановки можна записати
потрібним списком. Аналогічні міркування
застосуємо для тих перестановок, що
починаються з 2, 3, ...,
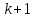 .
.
На стикуванні отриманих груп перестановок першу перестановку наступної групи отримаємо з останньої за рахунок транспозиції символів, що є першими у цих групах.
Теорему доведено.
Означення 3. Два
символи
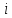 та
та
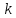 складають інверсію, якщо
складають інверсію, якщо
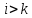 ,
але в перестановці знаходиться раніше.
,
але в перестановці знаходиться раніше.
Означення 4. Перестановка називається парною, якщо загальна кількість інверсій в ній парна, і непарною в протилежному випадку.
Теорема 3. Кожна транспозиція змінює парність перестановки.
Доведення.
При доведенні слід розглянути 2 випадки.
-
Елементи
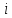 та
та
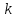 ,
над якими здійснюється транспозиція,
знаходяться поруч:
,
над якими здійснюється транспозиція,
знаходяться поруч:
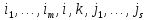
Зауважимо,
що після транспозиції положення
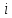 та
та
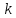 відносно інших елементів не зміниться.
Таким чином, якщо
відносно інших елементів не зміниться.
Таким чином, якщо
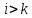 ,
то вони створюють інверсію і після
транспозиції інверсій стане на одну
менше. Якщо
,
то вони створюють інверсію і після
транспозиції інверсій стане на одну
менше. Якщо
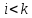 ,
то загальна кількість інверсій навпаки
збільшиться на одну.
,
то загальна кількість інверсій навпаки
збільшиться на одну.
Отже парність перестановки змінюється.
-
Між елементами
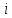 та
та
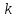 ,
над якими здійснюється транспозиція,
знаходяться інші елементи:
,
над якими здійснюється транспозиція,
знаходяться інші елементи:
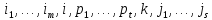
Зробимо транспозицію поступово.
Будемо
міняти місцями
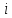 та сусідній справа, поки
та сусідній справа, поки
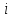 не поміняється із
не поміняється із
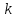 .
Для цього буде необхідно зробити t+1
транспозицій.
.
Для цього буде необхідно зробити t+1
транспозицій.
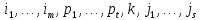
Щоб
поставити
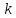 на місце
на місце
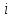 ,
необхідно зробити
,
необхідно зробити
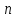 транспозицій із сусідами зліва. Загалом
буде зроблено 2t+1
транспозицій із сусідами зліва. Загалом
буде зроблено 2t+1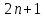 транспозицій, тобто в
наслідок попереднього випадку
парність перестановки змінюється.
транспозицій, тобто в
наслідок попереднього випадку
парність перестановки змінюється.
Теорему доведено.
Теорема 4.
При n≥2 кількість
парних перестановок дорівнює кількості
непарних перестановок, тобто
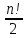 .
.
Доведення.
Запишемо всі
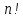 перестановок так, як це пропонує теорема
2 . Тоді за теоремою З у цьому списку буде
чергування парних і непарних перестановок.
перестановок так, як це пропонує теорема
2 . Тоді за теоремою З у цьому списку буде
чергування парних і непарних перестановок.
При
n≥2
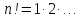 – парне число, тому список має парну
кількість перестановок, половина з яких
є парними, половина – непарними.
– парне число, тому список має парну
кількість перестановок, половина з яких
є парними, половина – непарними.
Теорему доведено.
