Плоское напряженное состояние.

При расчете или проверке на прочность базовым является так называемый критерий (условие) прочности. Но чтобы сформулировать этот критерий нужно разобраться в том, что происходит в точках нагруженного твердого тела.

Ранее мы выяснили, что в нагруженном объекте происходит взаимодействие всевозможных смежных объемов по границе их контакта. Границу мы ассоциируем с достаточно малой в размерах плоской площадкой. На таких площадках смежные (прилегающие) объемы находятся в силовом взаимодействии. Такое взаимодействие может быть охарактеризовано (описано) вектором полного напряжения в каждой точке и на всевозможных площадках. Причем если мы зафиксируем некоторую точку нагруженного тела, то при изменении ориентации площадки изменяется и вектор полного напряжения. Это значит, что в данной точке действует бесконечное число векторов полного напряжения. Кроме того, для фиксированной точки и фиксированной площадки вектор можно разложить на две составляющие и , то есть вводится понятие нормального и касательного напряжения на площадке.

Определение. Напряженным состоянием в точке называют совокупность напряжений (нормальных и касательных) действующих по всевозможным площадкам, проведенным в этой точке.

Методологически целесообразно различать и отдельно рассматривать несколько видов напряженного состояния. Вводится понятие трех взаимно перпендикулярных площадок в точке (фактически вводится база трехмерного пространства). Такие площадки удобнее всего представлять как грани бесконечно малого (элементарного) параллелепипеда. Каждую пару параллельных граней можно представлять как одну площадку с двумя сторонами.

Каждый вид напряженного состояния характеризуется определенной совокупностью напряжений, действующих на грани элементарного параллелепипеда (т. е. на трех взаимно перпендикулярных площадках), определенным образом сориентированного.

Наиболее простым видом является линейное (одноосное) наряженное состояние. Линейное напряженное состояние имеет место в растянутых или сжатых стержнях. Оно было подробно изучено ранее в разделе стержни. Если в окрестности некоторой точки выделить («вырезать») элементарный параллелепипед, две грани которого перпендикулярны линии действия приложенной силы, то напряжения будут действовать только на двух гранях, все остальные будут свободны от напряжений. То есть из трех взаимно перпендикулярных площадок в точке нагруженной будет только одна (она совпадает с поперечным сечением). Причем на ней действует только нормальное напряжение.

Плоское (двухосное) напряженное состояние характерно тем, что напряжения действуют уже на двух парах параллельных граней элементарного параллелепипеда. Примером объекта работающего в условиях плоского напряженного состояния может служить пластина, нагруженная силами в плоскости пластины. Кроме того, на гранях параллелепипеда действуют как нормальные, так и касательные напряжения.

Самый общий вид это объемное (трехосное) напряженное состояние. Оно характеризуется тем, что в точках нагруженного объекта напряжения действуют на всех трех взаимно перпендикулярных площадках при любой их ориентации.

Нам предстоит подробно изучить плоское напряженное состояние. Дело обстоит так. Пусть в точке выбраны три площадки, нормалями к которым служат оси координат . На одной из этих площадок (с нормалью ) напряжения отсутствуют. На двух других напряжения считаются известными. Требуется определить напряжения на любой наклонной площадке по отношению к площадкам с нормалями и (т. е. и ).

Определим напряжения на наклонной площадке.

Ввиду малости размеров площадок считаем, что напряжения на них распределены равномерно:

(1)

(2)

(3)

Из последнего уравнения (3) следует закон парности касательных напряжений

(4)

Касательные напряжения на двух взаимно-перпендикулярных площадках равны по величине и противоположены по знаку.

Два первых уравнения равновесия дают:

(5)

Учитывая что , (6)

и поделив оба уравнения на размер , получим:

или окончательно:

(7)

Эти формулы позволяют определить значения нормальных и касательных напряжений на любых площадках, проходящих через данную точку, если известны напряжения и .

Пусть , тогда учитывая что

, , ,

получаем

Из двух последних равенств следует что , а из двух первых имеем .

То есть если поворачивать две взаимно перпендикулярные площадки вокруг оси , то нормальные и касательные напряжения на них изменяются. Но при этом сумма нормальных напряжений на любых двух взаимно-перпендикулярных площадках остается постоянной и выполняется закон парности касательных напряжений.

ГЛАВНЫЕ НАПРЯЖЕНИЯ. ГЛАВНЫЕ ПЛОЩАДКИ

При реальных инженерных расчетах определить напряжения на всех площадках, проходящих через данную точку невозможно. В этом и нет необходимости. Из всего множества значений напряжений достаточно знать экстремальные (т.е. макс. и мин.) их значения.

Максимальные и минимальные нормальные напряжения называются главными напряжениями, а площадки, на которых они действуют, называются главными площадками.

Для определения главных напряжений решаем задачу экстремума для функции , приравнивая нулю производную по:

.

То есть

, (8)

где - угол наклона главной площадки по отношению к площадке, на которой действует напряжение .

Можно заметить что,

.

Следовательно, на главных площадках касательное напряжение равно нулю.

Далее из соотношения (8) выражаем

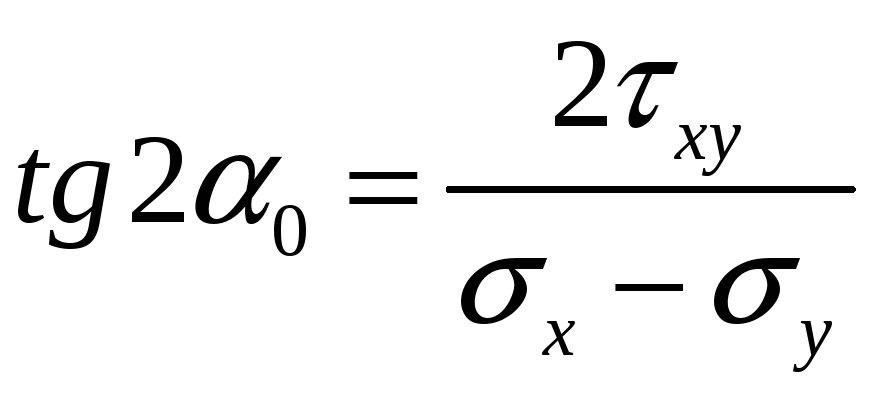(9)

Это уравнение дает два значения угла .

Угол положительный, когда площадку, где действует надо повернуть на этот против часовой стрелки, чтобы она стала главной.

Теперь определяем главные напряжения в рассматриваемой точке. Для этого используем первую формулу (7):

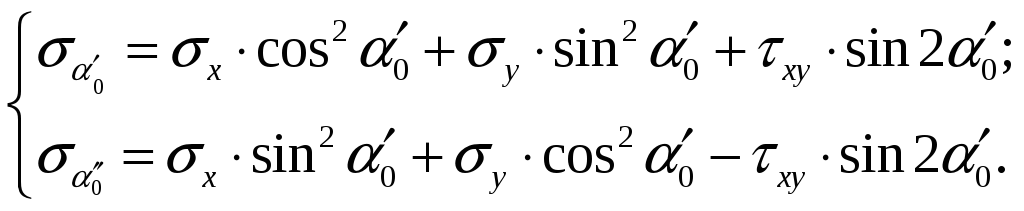(10)

Одно из этих напряжений максимальное, а другое минимальное в данной точке. Если требуется определить главные напряжения в точке, не устанавливая положение главных площадок, то можно использовать формулу

. (11)

Главные напряжения принято обозначать: ; .

Если совместить направление главных напряжений с направлением осей координат, то на основании (7) можно записать формулы, по которым можно вычислить напряжения на наклонных площадках по отношению к главным площадкам

(12)

Экстремальные касательные напряжения.

Согласно (7) при изменении положения площадок меняются как нормальное, так и касательное напряжения. Следовательно, правомерен вопрос об экстремальных касательных напряжениях в точке и положении площадок, на которых они действуют. Решаем задачу экстремума для функции:

,

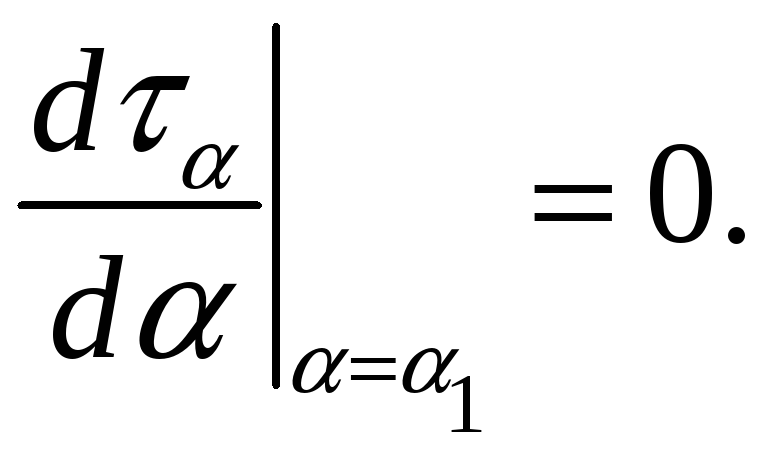
или .

Откуда выражаем

. (13)

Отсчет угла такой же, как и для угла. Уравнение (13) также дает два решения для угла и . На одной из площадок действует , а на другой . Из закона парности следует, что

Сравнивая выражения для и , отмечаем что

.

Разрешая это тригонометрическое уравнение, получаем:

;

; или .

Полученный результат означает что площадки, на которых касательные напряжения экстремальны (площадки сдвига) повернуты по отношению к главным площадкам под углом . То есть, если известно положение главных площадок в точке, то известно и положение площадок сдвига.

Графический метод определения на наклонных площадках.

Вычислениеи в зависимости от главных напряжений может быть проведено и графически.

На отрезке АВ как на диаметре строим круг с центром в точке С. Этот круг называется кругом напряжений. Для определения нормального напряжения и касательное напряжение по площадке, нормаль которого составляет с наибольшим главным напряжением , угол , надо построить в точке С центральный угол .

Тогда координаты точки D соответственно равныи.

изимеем

Лекция № 13

Объемное напряженное состояние

Наиболее общим типом напряженного состояния является объемное (или трехосное) напряженное состояние. Через данную точку нельзя провести ни одной площадки, напряжения на которой были бы ровны нулю в отличие от линейного и плоского напряженного состояния. Если в окрестности, какой - либо точки нагруженного тела взять элементарный параллелепипед, то на его гранях будут действовать девять компонентов напряжений. Если эти компоненты записать в таблицу, то получим так называемый тензор напряжений.

(1)

В случае объемного напряженного состояния также выполняется закон парности касательных напряжений.

(2)

Таким образом, тензор напряжений (1) имеет 6 независимых компонентов. Другими словами, напряженное состояние в какой-либо точке считается известными, если известны 6 компонентов напряжений, действующих на трех взаимно перпендикулярных площадках (т.е. известен тензор напряжений).

Главные площадки. Главные напряжения.

Напряжения на любой наклонной площадке с нормалью выражаются через напряжения и углы между нормалью и осями Среди множества наклонных площадок существуют такие на которых , а .Эти площадки называются главными, и нормальные напряжения на них – главными напряжениями.

Посмотрим как определяются главные напряжения через напряжения действующие на площадках с нормалями Предположим, что ориентация главной площадки нам известна. Тогда сечение параллельное главной площадки имеет нормаль и отсекает от граней элементарного параллелепипеда треугольные участки. Получим фигуру – «тетраэдр».

Обозначим:

(3)

Рассмотрим уравнение равновесия полученного тетраэдра, спроектировав все силы на каждой из осей. Сила, действующая на наклонной площадке равна , где – площадь наклонной площадки, учитывая (3) получим выражения для других площадей:

, ,

Силы, действующие на эти площадки, есть напряжения на площадь грани.

Сумма проекций на ось дает:

(5)

Получим систему уравнений относительно главных напряжений.

Т.к. , все они нулю одновременно равняться не могут. Чтобы существовало решение системы (5) необходимо равенство нулю определителем.

(6)

Раскрыв определитель, получим кубическое уравнение.

(7)

Три корня полученного уравнения дают три главных напряжения .

Коэффициенты – называются инвариантами напряженного состояния и имеют вид:

(8)

Условием о правилах обозначений главных напряжений.

Максимальные касательные напряжения.

В окрестности каждой точки существует три площадки на которых касательные напряжения принимают экстремальное значение (площадки сдвига).

Используем понятие плоского напряженного состояния, можно получить:

Т.к.

(10)

Определение напряжений на площадках наклоненных по отношению к главным площадкам. Пусть главные напряжения известны. Найти напряжение на площадке с нормалью .

Если площадь наклонной площадки равна , то площади других граней тетраэдра равны:

; ;

Спроектировав все силы, действующие на тетраэдр на нормаль , получим:

или:

(11)

Для определения сначала определим полное напряжение на наклонной площадке. Оно равно равнодействующей от напряжений

и

(12)