
- •Часть 1
- •Часть 1
- •Общие указания по выполнению расчетно-графических работ
- •Используемые обозначения
- •1. Растяжение-сжатие
- •Основные понятия и формулы
- •1.1. Расчет статически определимых стержневых систем Основные определения
- •1.1.2. Определение напряжений и перемещений в стержне при растяжении-сжатии с учетом собственного веса (задача № 2) Условие задачи
- •Решение
- •1.1.3. Определение грузоподъемности статически определимой конструкции, работающей на растяжение-сжатие (задача № 3) Условие задачи
- •Решение
- •1.2. Расчет статически неопределимых стержневых систем Основные определения
- •Решение
- •1.2.2. Расчет статически неопределимой стержневой конструкции, работающей на растяжение-сжатие (задача № 5) Условие задачи
- •Часть 2. Расчет по предельному пластическому состоянию. Требуется найти грузоподъемность (или подобрать сечения стержней) расчетом по предельному состоянию.
- •Решение
- •Часть 1. Для расчета конструкции по упругой стадии деформации необходимо составить три группы уравнений:
- •1.2.3. Определение грузоподъемности статически неопределимой шарнирно-стержневой конструкции (задача № 6) Условие задачи
- •В задаче № 6
- •Решение
- •2. Исследование плоского напряженного состояния. Проверка прочности для сложного напряженного состояния
- •Основные понятия и формулы
- •Решение
- •Условия задачи Решение
- •Условие задачи
- •Решение
- •3. Кручение
- •Основные понятия и формулы
- •Решение
- •3.2. Расчет статически неопределимого вала при кручении (задача № 11) Условие задачи
- •Решение
- •Список литературы
- •Содержание
- •Сопротивление материалов
- •Часть 1
-
найти нормальное
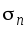 ,
касательное
,
касательное
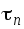 и полное
и полное
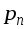 напряжения на наклонной площадке,
заданной углом
напряжения на наклонной площадке,
заданной углом
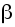 и изображенной на рис. 2.14;
и изображенной на рис. 2.14; -
найти величины наибольшего касательного напряжения и соответствующего ему нормального напряжения, показать положение площадки, на которой эти напряжения действуют;
-
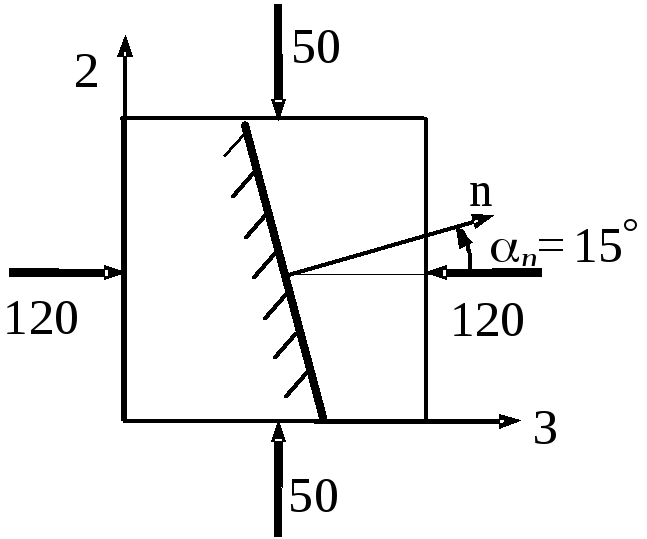
Рис. 2.15. Уточнение
Условия задачи Решение
проверить прочность материала; найти действительный коэффициент запаса прочности.
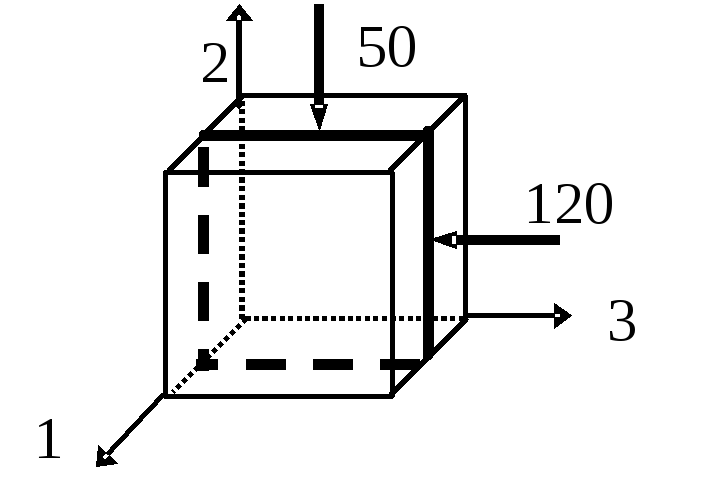
Заданный элемент ограничен главными
площадками, поэтому сразу нумеруем
главные напряжения по убыванию (![]() ,
,
![]() МПа,
МПа,
![]() МПа)
и изображаем на рисунке главные оси
(рис. 2.15).
МПа)
и изображаем на рисунке главные оси
(рис. 2.15).
Определение напряжений.
Напряжения на наклонной площадке
вычисляются так же, как в задаче № 7.
Единственное отличие состоит в том, что
можно использовать частный случай (2.4)
общих формул (2.2а) и (2.2б). Положение
наклонной площадки будем задавать углом
![]() ,
отсчитываемым от оси 3 к нормали n.
Значение
,
отсчитываемым от оси 3 к нормали n.
Значение
![]() положительно, так как угол отсчитывается
против часовой стрелки.
положительно, так как угол отсчитывается
против часовой стрелки.
Согласно (2.4)
![]()
![]()
Модуль полного напряжения
![]() МПа.
МПа.
Примененная формула для касательного
напряжения
![]() справедлива для площадок, перпендикулярных
плоскости чертежа. Максимальное для
таких площадок касательное напряжение
справедлива для площадок, перпендикулярных
плоскости чертежа. Максимальное для
таких площадок касательное напряжение
![]() МПа.
МПа.
Соответствующее нормальное напряжение
Рис. 2.17. Площадка
с максимальным
касательным напряжением
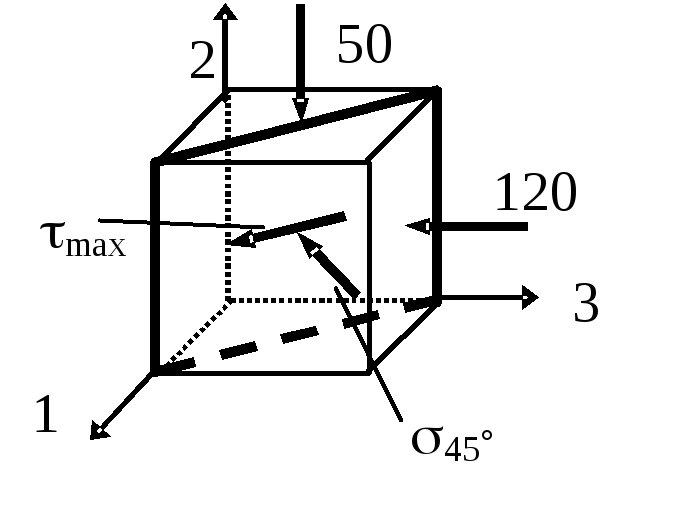
![]()
![]() МПа.
МПа.
Рис. 2.16. Площадка
с максимальным
касательным напряжением
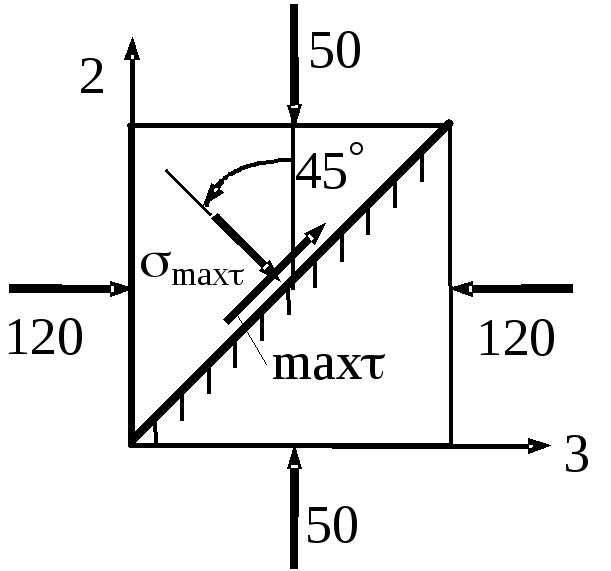
![]()
![]() не самое большое из всех возможных
значений. Это значение является максимумом
для касательных напряжений по площадкам,
перпендикулярным плоскости чертежа.
Площадка, на которой действует
не самое большое из всех возможных
значений. Это значение является максимумом
для касательных напряжений по площадкам,
перпендикулярным плоскости чертежа.
Площадка, на которой действует
![]() ,
расположена под углом 45°
к главным площадкам 2, 3 (рис. 2.16).
,
расположена под углом 45°
к главным площадкам 2, 3 (рис. 2.16).
Максимальное касательное напряжение (максимум вычисляется для всех возможных площадок, проведенных через точку) и соответствующее ему нормальное напряжение имеют величины
![]() МПа,
МПа,
![]() МПа
МПа
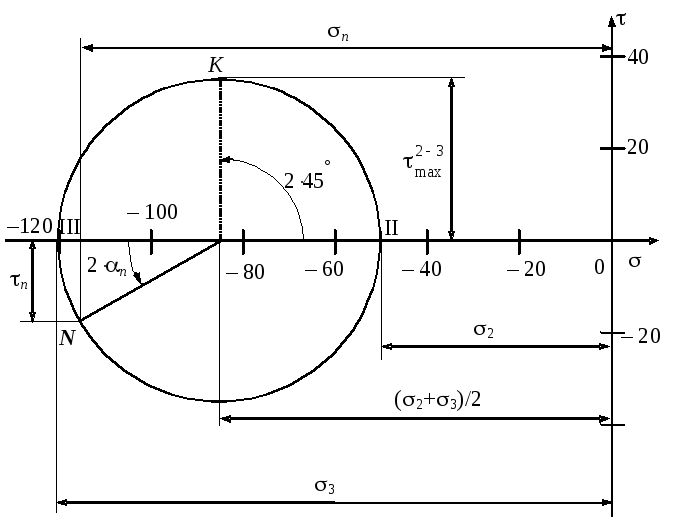
Рис. 2.18. Круг Мора,
изображающий заданное плоское
напряженное
состояние
![]() .
.
Круг напряжений для заданного плоского
напряженного состояния показан на
рис. 2.18. Координаты точки
![]() дают значение напряжений на площадке
с нормалью n. Площадке
с
дают значение напряжений на площадке
с нормалью n. Площадке
с
![]() соответствует точка
соответствует точка
![]() круга.
круга.
Рис. 2.19. Круги
Мора,
изображающие
объемное
напряженное
состояние
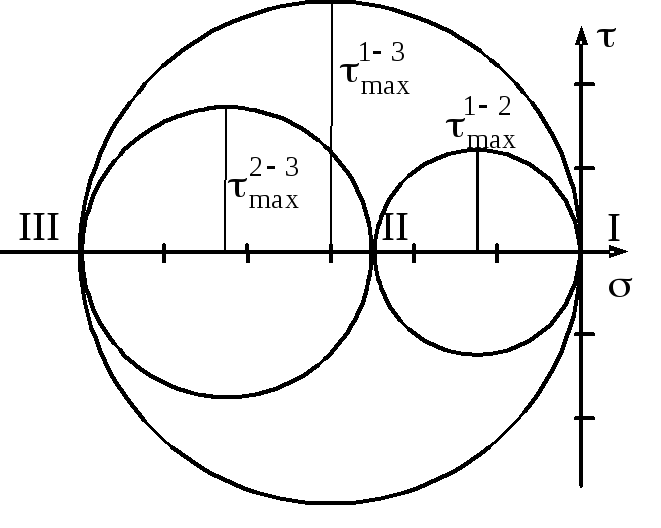
![]() соответствует точка, лежащая на бóльшем
круге напряжений.
соответствует точка, лежащая на бóльшем
круге напряжений.
Проверка прочности. По условию задачи материал элемента хрупкий. При проверке прочности используем теории прочности, относящиеся к хрупким материалам.
Расчетное напряжение, соответствующее первой теории прочности
![]() .
.
Видим, что первая теория прочности не годится для оценки прочности, так как она выдает в рассматриваемой ситуации неправдоподобный результат: при любом уровне напряжений прочность обеспечена.
Расчетное напряжение по второй теории прочности:
![]()
Прочность обеспечена с фактическим коэффициентом запаса
![]() ,
,
большем нормативного (![]() ).
).
Расчетное напряжение по теории прочности Мора,
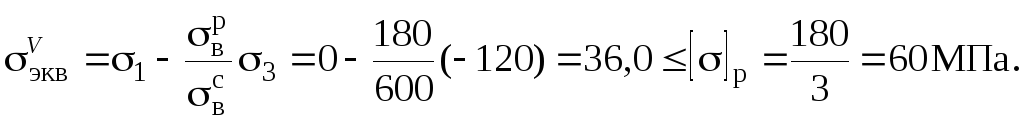
Прочность обеспечена. Фактический коэффициент запаса таков:
![]() .
.
Рис. 2.20. Опасная
площадка
по первой и второй
теориям
прочности
![]() раз), то по указанной плоскости произойдет
разрушение.
раз), то по указанной плоскости произойдет
разрушение.
2.3. РАСЧЕТ ТОНКОСТЕННОЙ ТРУБЫ,
ПОДВЕРЖЕННОЙ ДЕЙСТВИЮ ВНУТРЕННЕГО ДАВЛЕНИЯ, ПРОДОЛЬНОЙ СИЛЫ И КРУТЯЩЕГО МОМЕНТА
(ЗАДАЧА № 9)
Основные формулы
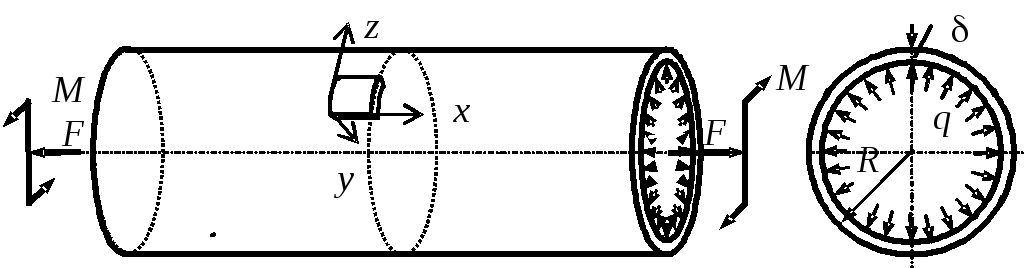
Рис. 2.21. Тонкостенная
труба под действием внутреннего
давления, продольной
силы и крутящего момента
![]() .
Отношение длины l к
радиусу
.
Отношение длины l к
радиусу
![]() .
Труба нагружена внутренним давлением
.
Труба нагружена внутренним давлением
![]() ,
по ее торцам приложены силы
,
по ее торцам приложены силы
![]() и крутящие моменты
и крутящие моменты
![]() .
.
Напряжения в трубе обозначаем, используя местную декартову систему координат x, y, z: ось x параллельна оси трубы, ось z направлена по касательной к срединной линии поперечного сечения, осью y служит продолжение радиуса R.
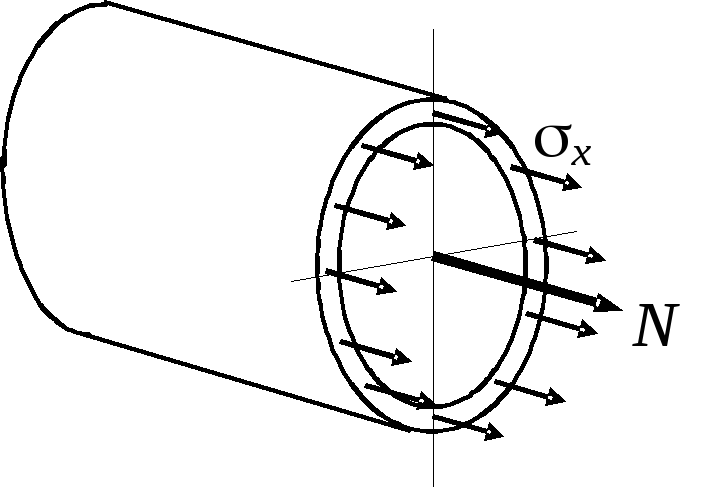
Сила
![]() вызывает в поперечном сечении трубы
продольное усилие
вызывает в поперечном сечении трубы
продольное усилие
![]() и создает нормальное напряжение
(рис. 2.22)
и создает нормальное напряжение
(рис. 2.22)
![]() .
.
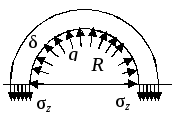
Рис. 2.23. Напряжения
в трубе
от внутреннего
давления
![]() – площадь поперечного сечения тонкостенной
трубы.
– площадь поперечного сечения тонкостенной
трубы.
Рис. 2.22. Напряжения
в трубе от продольной
силы
![]() в продольных сечениях трубы:
в продольных сечениях трубы:
![]() .
.
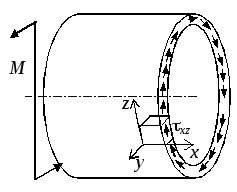
Рис. 2.24. Напряжения
в трубе от крутящего
момента
![]() положительны при
положительны при
![]() .
Случай
.
Случай
![]() отвечает давлению, приложенному к
наружной поверхности.
отвечает давлению, приложенному к
наружной поверхности.
Крутящий момент создает касательные напряжения (рис. 2.24):
![]() .
.
Они направлены так, чтобы уравновесить пару сил М.
По толщине трубы напряжения
![]() распределены равномерно. Остальные
напряжения либо в точности равны нулю,
либо малы:
распределены равномерно. Остальные
напряжения либо в точности равны нулю,
либо малы:
![]() ,
,
![]() .
.
Напряженное состояние элементарного параллелепипеда, вырезанного из трубы (рис. 2.25), является плоским. Анализ напряженного состояния выполняется так же, как в задаче № 7.
