
- •Введение
- •1. Цель работы
- •2. Основные понятия о векторах
- •3. Критерий равенства двух векторов
- •4. Координаты точек на прямой, плоскости и в пространстве
- •5. Две теоремы о проекции вектора на ось
- •6. Сложение векторов
- •7. Умножение вектора на скаляр
- •8. Линейно зависимые и линейно независимые векторы
- •9. Разложение вектора по координатным ортам
- •10. Критерии коллинеарности двух векторов
- •11. Деление отрезка в данном отношении
- •12. Скалярное произведение двух векторов
- •13. Понятие векторного произведения двух векторов
- •14. Смешанное произведение трёх векторов
- •15. Свойства векторного произведения двух векторов
- •16. Представление смешанного произведения трёх векторов через проекции перемножаемых векторов на коордонатные оси
- •17. Двойное векторное произведение трёх векторов
- •18.Угол между векторами
- •19. Критерий коллинеарности двух векторов
- •20. Критерии перпендикулярности двух векторов
- •21. Критерии компланарности трёх векторов
- •23. Площадь треугольника
10. Критерии коллинеарности двух векторов
Первый критерий коллинеарности двух векторов
Для того чтобы два ненулевых вектора были коллинеарны, необходимо и достаточно, чтобы эти векторы были линейно зависимы.
Доказательство.
(Необходимость) По условию векторы
![]() и
и
![]() коллинеарны. При этом возможны два
случая:
коллинеарны. При этом возможны два
случая:
1.
![]() .
Тогда, по теореме об одинаково направленных
векторах,
.
Тогда, по теореме об одинаково направленных
векторах,
![]() ,
т.е.
,
т.е.
![]() ,
где
,
где
![]() .
.
2.
![]() .
В этом случае, используя теорему о
противоположно направленных векторах,
имеем
.
В этом случае, используя теорему о
противоположно направленных векторах,
имеем
![]() ,
т.е.
,
т.е.
![]() .
Здесь
.
Здесь
![]() .
.
Итак,
если векторы
![]() и
и
![]() коллинеарны, то существует такое число
коллинеарны, то существует такое число
![]() ,
что
,
что
![]() ,
а это равенство, согласно критерию
линейной зависимости векторов, означает,
что векторы
,
а это равенство, согласно критерию
линейной зависимости векторов, означает,
что векторы
![]() и
и
![]() линейно зависимы. Отсюда, в частности,
следует, что любые два вектора,
расположенные на одной прямой, линейно
зависимы.
линейно зависимы. Отсюда, в частности,
следует, что любые два вектора,
расположенные на одной прямой, линейно
зависимы.
(Достаточность.)
Пусть векторы
![]() и
и
![]() линейно зависимы. Тогда
линейно зависимы. Тогда
![]() ,
где
,
где
![]() - некоторое число. Согласно определению
произведения вектора на скаляр,
направление вектора
- некоторое число. Согласно определению
произведения вектора на скаляр,
направление вектора
![]() в зависимости от знака скаляра
в зависимости от знака скаляра
![]() либо совпадает с направлением вектора
либо совпадает с направлением вектора
![]() либо противоположно направлению вектора
либо противоположно направлению вектора
![]() ,
т.е. вектор
,
т.е. вектор
![]() ,
равный
,
равный
![]() ,
коллинеарен вектору
,
коллинеарен вектору
![]() .
.
Второй критерий коллинеарности двух векторов
Для
того, чтобы два ненулевых вектора были
коллинеарны, необходимо и достаточно,
чтобы одноименные проекции этих векторов
на координатные оси были пропорциональны:
![]() .
.
Пропорции
![]() формально теряют силу, когда хотя бы
один из знаменателей обращается в нуль.
Более общей является следующая форма
записи факта пропорциональности
одноименных проекций рассматриваемых
векторов на координатные оси:
формально теряют силу, когда хотя бы
один из знаменателей обращается в нуль.
Более общей является следующая форма
записи факта пропорциональности
одноименных проекций рассматриваемых
векторов на координатные оси:
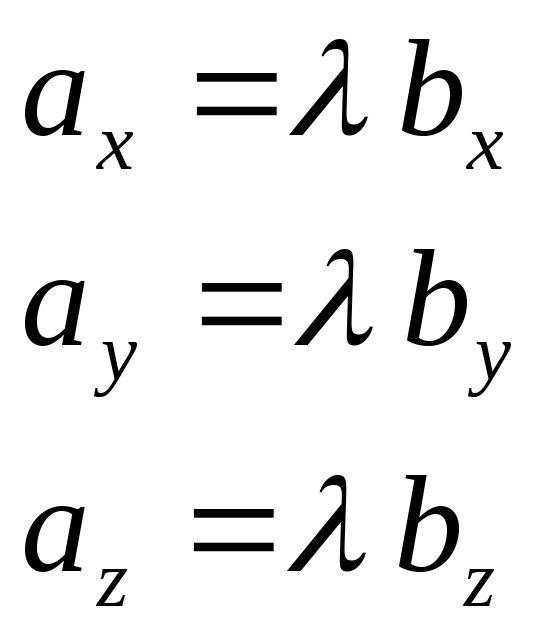
Однако
часто используют пропорции
![]() .
.
При этом предполагается, что если какой-либо из знаменателей равен нулю, то и соответствующий числитель тоже равен нулю.
Доказательство.
(Необходимость) Если векторы
![]() и
и
![]() коллинеарны, то согласно первому критерию
коллинеарности двух векторов, векторы
коллинеарны, то согласно первому критерию
коллинеарности двух векторов, векторы
![]() и
и
![]() линейно зависимы, а потому
линейно зависимы, а потому
![]() .
Из этого равенства следует, что
.
Из этого равенства следует, что
![]() ,
т.е.
,
т.е.
![]() .
.
(Достаточность)
Пусть
![]()
Положим
каждое из этих отношений равным
![]() .
Тогда
.
Тогда
![]() .
.
Если
же наряду с этими равенствами
воспользоваться теоремой о разложении
вектора по координатным ортам
![]() ,
то получим
,
то получим
![]() ,
или, согласно свойствам операции
умножения вектора на скаляр,
,
или, согласно свойствам операции
умножения вектора на скаляр,
![]() ,
т.е.
,
т.е.
![]() .
.
Следовательно,
векторы
![]() и
и
![]() линейно зависимы, и потому, согласно
первому критерию коллинеарности двух
векторов, векторы
линейно зависимы, и потому, согласно
первому критерию коллинеарности двух
векторов, векторы
![]() и
и
![]() коллинеарны, что и требовалось доказать.
коллинеарны, что и требовалось доказать.
11. Деление отрезка в данном отношении
Определение.
Говорят, что точка
![]() делит отрезок, соединяющий точки
делит отрезок, соединяющий точки
![]() и
и
![]() ,
в данном отношении
,
в данном отношении
![]() ,
если вектор
,
если вектор
![]() равен произведению вектора
равен произведению вектора
![]() на число
на число
![]() ,
т.е.
,
т.е.
![]() .
.
Согласно
определению, точка
![]() делит отрезок, соединяющий точки
делит отрезок, соединяющий точки
![]() и
и
![]() в данном отношении
в данном отношении
![]() если
если
1)
точка
![]() лежит на прямой, проходящей через точки
лежит на прямой, проходящей через точки
![]() и
и
![]() ,
причем
,
причем
а ) точка
) точка
![]() лежит между точками
лежит между точками
![]() и
и
![]() ,
при
,
при
![]() ,
,
б ) точка
) точка
![]() лежит вне отрезка, соединяющего точки
лежит вне отрезка, соединяющего точки
![]() и
и
![]() ,
при
,
при
![]()
2)![]()
При
этом разумеется, что точка
![]() не совпадает ни с одной из точек
не совпадает ни с одной из точек
![]() и
и
![]()
Теорема.
Если точка
![]() делит отрезок, соединяющий точки
делит отрезок, соединяющий точки
![]() и
и
![]() в данном отношении
в данном отношении
![]() ,
причем
,
причем
![]() ,
то для координат точки
,
то для координат точки
![]() справедливы следующие равенства:
справедливы следующие равенства:
![]() ;
; ![]() ;
; ![]()
Доказательство.
Пусть точка
![]() делит отрезок, соединяющий точки
делит отрезок, соединяющий точки
![]() и
и
![]() ,
в данном отношении
,
в данном отношении
![]() .
Тогда по определению
.
Тогда по определению
![]() ,
и потому по отношению к любой оси
,
и потому по отношению к любой оси
![]() справедливо равенство
справедливо равенство
![]()
![]() ,
,
или, с учетом теоремы о проекции на ось произведения вектора на скаляр,
![]()
![]() .
.
Возьмем
в качестве оси
![]() ось
ось
![]() и применим теорему о проекции вектора
на числовую ось. При этом получим
и применим теорему о проекции вектора
на числовую ось. При этом получим
![]() ,
,
откуда следует, что
![]() .
.
Вполне аналогично можно доказать справедливость остальных равенств, указанных в формулировке теоремы.
Частный
случай. Координаты
точки, делящей отрезок пополам (при этом
![]() ),
равны среднему арифметическому
соответствующих одноименных координат
концов отрезка, т.е.
),
равны среднему арифметическому
соответствующих одноименных координат
концов отрезка, т.е.
![]() ;
; ![]() ;
; ![]() .
.
