
- •Введение
- •1. Цель работы
- •2. Основные понятия о векторах
- •3. Критерий равенства двух векторов
- •4. Координаты точек на прямой, плоскости и в пространстве
- •5. Две теоремы о проекции вектора на ось
- •6. Сложение векторов
- •7. Умножение вектора на скаляр
- •8. Линейно зависимые и линейно независимые векторы
- •9. Разложение вектора по координатным ортам
- •10. Критерии коллинеарности двух векторов
- •11. Деление отрезка в данном отношении
- •12. Скалярное произведение двух векторов
- •13. Понятие векторного произведения двух векторов
- •14. Смешанное произведение трёх векторов
- •15. Свойства векторного произведения двух векторов
- •16. Представление смешанного произведения трёх векторов через проекции перемножаемых векторов на коордонатные оси
- •17. Двойное векторное произведение трёх векторов
- •18.Угол между векторами
- •19. Критерий коллинеарности двух векторов
- •20. Критерии перпендикулярности двух векторов
- •21. Критерии компланарности трёх векторов
- •23. Площадь треугольника
9. Разложение вектора по координатным ортам
Теорема.
Всякий вектор
![]() может быть представлен в виде линейной
комбинации всех координатных ортов с
проекциями рассматриваемого вектора
на соответствующие координатные оси,
т.е.
может быть представлен в виде линейной
комбинации всех координатных ортов с
проекциями рассматриваемого вектора
на соответствующие координатные оси,
т.е.
![]() .
.
Здесь
используются обозначения:
![]() ,
,
![]() ,
,
![]()
Доказательство.
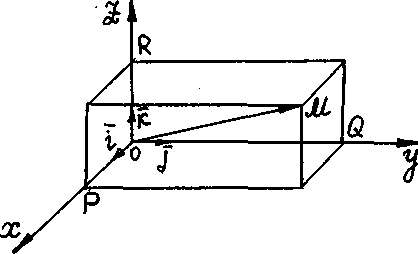
Совместим
начало вектора
![]() с началом декартовой системы координат,
т.е. построим вектор
с началом декартовой системы координат,
т.е. построим вектор
![]() такой, что
такой, что
![]() .
.
Построим
составляющие вектора
![]() по координатным осям:
по координатным осям:
![]() ,
, ![]() ,
, ![]() .
.
Согласно определению суммы векторов,
![]()
![]()
![]()
![]() ,
,
или,
что то же самое,
![]()
![]()
![]()
![]() .
.
Если
применить теперь теорему о связи между
составляющей вектора по оси и ортом
этой оси, то получим
![]()
![]()
![]()
![]() т.е.
т.е.
![]() что и требовалось доказать.
что и требовалось доказать.
Теорема. Разложение вектора по координатным ортам единственно.
Доказательство.
Пусть
![]() .
Покажем, что
.
Покажем, что
![]() ,
,
![]() ,
,
![]() Вычислим проекцию вектора
Вычислим проекцию вектора
![]() на ось
на ось
![]() .
На основании теоремы о проекции суммы
векторов на ось
.
На основании теоремы о проекции суммы
векторов на ось
![]() .
.
Воспользуемся
теоремой о проекции на ось произведения
вектора на скаляр. Тогда получим
![]() .
Так как
.
Так как
![]() ,
,
![]() ,
,
![]() ,
то имеем
,
то имеем
![]() и потому
и потому
![]() .
.
Аналогично
можно доказать, что
![]() и
и
![]()
Разложение орта вектора по координатным ортам
Определение.
Направляющими косинусами вектора
![]() называются косинусы углов между
координатными осями и рассматриваемым
вектором
называются косинусы углов между
координатными осями и рассматриваемым
вектором
![]() ,
т.е.
,
т.е.
![]() ,
,
![]() ,
,
![]() .
.
Теорема.
Орт вектора может быть представлен в
виде линейной комбинации координатных
ортов с соответствующими направляющими
косинусами этого вектора, т.е.
![]()
Доказательство. По теореме о разложении вектора по координатным ортам
![]()
![]()
![]()
![]() и
так как
и
так как
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
то
,
то
![]()
Разложение радиуса-вектора точки по координатным ортам
Теорема.
Радиус-вектор точки
![]() может быть представлен в виде линейной
комбинации координатных ортов с
декартовыми координатами точки
может быть представлен в виде линейной
комбинации координатных ортов с
декартовыми координатами точки
![]() ,
т.е.
,
т.е.
![]() ,
,
где
![]() - радиус-вектор точки
- радиус-вектор точки
![]() ,
,
![]() ,
,
![]() ,
,
![]() - декартовы координаты точки
- декартовы координаты точки
![]() .
.
Доказательство. Всякий вектор может быть представлен в виде:
![]() .
.
Применительно
к радиусу-вектору точки
![]() имеем
имеем
![]()
![]()
![]()
![]()
Согласно
определению декартовых координат точки
![]()
![]() ,
, ![]() ,
, ![]() ,
,
и
потому
![]() .
.
Разложение вектора ММ по координатным ортам
Теорема. Всякий вектор может быть представлен в виде линейной комбинации координатных ортов с разностями соответствующих одноименных координат конца и начала рассматриваемого вектора, т.е.
![]() .
.
где
![]() ,
,
![]() ,
,
![]() - декартовы координаты точки
- декартовы координаты точки
![]() ,
,
![]() ,
,
![]() ,
,
![]() -
декартовы координаты точки
-
декартовы координаты точки
![]() .
.
Доказательство. Согласно теореме о разложении вектора по координатным ортам, имеем
![]()
![]()
![]()
![]() ,
,
или, с учетом теоремы о проекции вектора на числовую ось,
![]() .
.
Утверждение доказано.
Определение.
Совокупность двух векторов
![]() и
и
![]() называется базисом плоскости, если
любой вектор, расположенный в плоскости
векторов
называется базисом плоскости, если
любой вектор, расположенный в плоскости
векторов
![]() и
и
![]() ,
может быть представлен в виде линейной
комбинации векторов
,
может быть представлен в виде линейной
комбинации векторов
![]() и
и
![]() с некоторыми числами
с некоторыми числами
![]() и
и
![]() ,
т.е. для любого вектора
,
т.е. для любого вектора
![]() ,
расположенного в плоскости векторов
,
расположенного в плоскости векторов
![]() и
и
![]() ,
существуют числа
,
существуют числа
![]() и
и
![]() такие, что
такие, что
![]() .
Можно доказать, что совокупность любых
двух неколлинеарных векторов является
базисом плоскости. Аналогично вводится
понятие базиса пространства.
.
Можно доказать, что совокупность любых
двух неколлинеарных векторов является
базисом плоскости. Аналогично вводится
понятие базиса пространства.
Определение.
Совокупность трех векторов
![]() ,
,
![]() и
и
![]() называется базисом пространства, если
любой вектор в пространстве может быть
представлен в виде линейной комбинации
векторов
называется базисом пространства, если
любой вектор в пространстве может быть
представлен в виде линейной комбинации
векторов
![]() ,
,
![]() и
и
![]() ,
с некоторыми числами
,
с некоторыми числами
![]() ,
,
![]() и
и
![]() ,
т.е. для любого вектора
,
т.е. для любого вектора
![]() в пространстве существуют числа
в пространстве существуют числа
![]() ,
,
![]() и
и
![]() ,
такие, что
,
такие, что
![]() .
.
В
теореме о разложении вектора по
координатным ортам было показано, что
для любого вектора
![]() справедливо равенство
справедливо равенство
![]() .
.
Следовательно,
совокупность ортов
![]() является базисом пространства.
является базисом пространства.
Можно доказать, что совокупность любых трех некомпланарных векторов является базисом пространства.
