Сведение произвольной системы ошибок стрельбы к схеме двух групп ошибок
>> n=length(R);rm=sqrt((sum(sum(R.^2))-n)/n/(n-1));
>> M=mean2(A); Sx=std2(A), Sxo=Sx* sqrt(rm), Sxio=sqrt(Sx^2-Sxo^2), rm
Sx = 10.3052 Sxo = 6.8932 Sxio = 7.6604 rm = 0.4474
Результаты Scatter2g получены точно так же, поэтому полностью совпадают:
>> Y= Yg +Yi, Yg,Yi, r
Norm_1 Y: MO = 12.027 CKO = 10.305
Norm_1 Yg: MO = 12.027 CKO = 6.893
Norm_1 Yi: MO = 0.000 CKO = 7.660
r = 0.4474
Ошибки стрельбы, моделирование которых осуществлялось по схеме четырех групп ошибок, корректно сведены к схеме двух групп ошибок, что позволяет вычислять вероятности поражения цели функцией W_r_n. Сравним оценки вероятности одного попадания по характеристическому массиву попаданий и с помощью объекта суммарных ошибок:
>> U=zeros(size(A));U(A>min(T) & A<max(T))=1; P=mean2(U),P_r=sum(sum(U,2)>0)/N
P = 0.1086 P_r = 0.6086
>> P=Ver(X,T), Pr=W_r_n(Yg,Yi,T,n)
P = 0.1087 Pr = 0.6121
Результаты вычислений по сведенной схеме двух групп ошибок практически совпадают со статистическими оценками, полученными обработкой большого объема прямых испытаний исходной модели стрельбы по схеме четырех групп ошибок. Это подтверждает корректность и правомерность использования статистического подхода.
Вычисление вероятности поражения цели в зависимых выстрелах
|
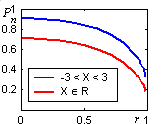
Рис. 8.6. Влияние корреляции на вероятность попадания |
>> Xg=Norm_1(0,8); Xi=Xg; X=Xg+Xi; T=[-3,3];net=[0.01:0.1:0.9 0.91:0.01:1];
>> p=[];for r=net p(end+1)= W_r_n(X,r,T,10);end, plot(net,p)
Объект двумерного нормального распределения создадим так, что его проекциями являются определенные выше одномерные СВ. Построим зависимость вероятности хотя бы одного попадания в прямоугольник 1010 той же циклической командой:
>> X2=Norm_2([Xg Xg])+Norm_2([Xi Xi]); R=RecShape([10 10]);
>> p=[];for r=net p(end+1)= W_r_n(X2,r,R,10);end,hold on, plot(net,p,'r')
Откуда берутся исходные данные о характеристиках ошибок стрельбы? Источники части индивидуальных ошибок – начальные возмущения при выстреле. Хотя они большей частью не зависят от конструкции снаряда, в конечном итоге влияние на рассеивание точки попадания зависит от баллистических характеристик снаряда. Поэтому индивидуальные ошибки необходимо рассматривать как функцию случайных величин – начальных возмущений.
Контрольные вопросы
-
Какими свойствами обладает функция распределения системы n СВ?
-
В чем принципиальное отличие системы n СВ от системы двух СВ?
-
Сколько информативных (не предопределенных) элементов содержится в матрице коэффициентов корреляции системы n СВ?
-
О чем говорит блочная структура матрицы коэффициентов корреляции системы n СВ?
-
Как можно получить корреляционную матрицу суммы некоррелированных случайных векторов?
-
Объясните случайную природу составляющих в схеме двух групп ошибок стрельбы. Чем они характеризуются?
-
Какова особенность матрицы коэффициентов корреляции индивидуальных ошибок рассеивания снарядов?
-
Какова особенность матрицы коэффициентов корреляции повторяющихся ошибок стрельбы?
-
Как вычислить вероятность хотя бы одного попадания в n зависимых выстрелах по схеме двух групп ошибок?
-
Объясните случайную природу составляющих в схеме трех групп ошибок стрельбы. Как вычислить вероятность поражения цели при такой схеме ошибок стрельбы?
-
Как вычисляют и используют сведенный коэффициент корреляции?
ПРИЛОЖЕНИЕ 8
Листинг 8.1. Файл-функция W_r_n для вычисления вероятности поражения в зависимых выстрелах по схеме двух групп ошибок:
function [W,r]=W_r_n(Xg,Xi,T,n,G)
if nargin<5 G=[]; end;
if length(G)==1 G=1-(1-G).^(1:n);
else G(end+1:n)=1;end
if isreal(Xi) [Xg,Xi]=VerDef(Xg,Xi); end
if isa(Xg, 'Norm_2')
[W,r]=W_r_n_2(Xg,Xi,T,n,G);
else
N=30;x=Net(Xg,[],[],N); K=1:min(n,length(G));
for i=1:N
p(i)=dot(p_Binom(Ver(Xi+x(i),T),n,1:n), G(1:n));
end
W=Trap(p.*f(Xg,x),x);
r=D(Xg)/D(Xg+Xi);
end
%
function [W,r]=W_r_n_2(Xg,Xi,T,n,G)
N=30;[a,b]=Net(Xg,N); K=1:min(n,length(G));
ni=length(a);nj=length(b);
for i=1:ni for j=1:nj
w=p_Binom(Ver(Xi+[a(i,j);b(i,j)],T),n,K);
p(i,j)=dot(w, G);
end,end
W=Trap2(p.*f(Xg,a,b),a,b);
[X1, X2]=X12(Xg);
[Y1, Y2]=X12(Xg+Xi);
r=D(X1)/D(Y1);
%
function [Xg,Xi]=VerDef(X,r)
if nargin<5 G=ones(1,n); end
if isa(X,'Norm_1')
[Xg, Xi]=Xgroup(X,r);
W=W_r_n(Xg,Xi,T,n,G);
return
end
[X1, X2]=X12(X);
[X1g, X1i]=Xgroup(X1,r);
[X2g, X2i]=Xgroup(X2,r);
Xg=Norm_2([X1g, X2g]);
Xi=Norm_2([X1i, X2i]);
%
function [Xg, Xi]=Xgroup(X,r)
Xg=X*sqrt(r);
Xi=Norm_1(0,sqrt(D(X)-D(Xg)));
Листинг 8.2. Универсальная файл-функция Scatter2g для моделирования ошибок стрельбы по схеме нескольких групп ошибок:
function [Xg,Xi,r,m,A]=Scatter2g(Xg,Xi,N,n,U)
if nargin<5 U={[],1}; end
if isa(Xg, 'Norm_2')
[Xg1, Xg2]=X12(Xg);
[Xi1, Xi2]=X12(Xi);
[X1g,X1i,r1,m,A]=F_Group(Xg1,Xi1,N,n,U);
[X2g,X2i,r2,m,A2]=F_Group(Xg2,Xi2,N,n,U);
Xg=Norm_2([X1g X2g]);
Xi=Norm_2([X1i X2i]);
r=sqrt(r1*r2);
else
[Xg,Xi,r,m,A]=F_Group(Xg,Xi,N,n,U);
end
%
function [Xg,Xi,r,m,A]=F_Group (Xg,Xi,N,n,U)
A=[]; M=size(U,1); L=n;
for k=1:M L=L*U{k,2}; end
A=Gen(Xi,N,L)+repmat(Gen(Xg,N,1),1,L);
for k=1:M
m=U{k,2};B=[];
for j=1:n:L
B=[B,repmat(Gen(U{k,1},N,1),1,n)];
end
A=A+B;n=n*m;
end
R=CorrelCoef(A); m=length(R);
r=sqrt((sum(sum(R.^2))-m)/m/(m-1));
M=mean2(A);S=std2(A); if abs(M)<0.001 M=0;end
X=Norm_1(M,S);
Xg = X*sqrt(r);
Xi=Norm_1(0,sqrt(D(X)- D(Xg)));
БЭСПиБП.8.
Система произвольного числа случайных
величин