Определение подходящего направления
Для описания алгоритма выбора наилучшего направления поиска очередной точки минимизирующей последовательности введём ряд важных понятий.
Определение 13.3.
Ограничение
![]() (
(
![]() ) называется
) называется
активным
в фиксированной точке
![]() ,
если
,
если
![]() (
(
![]() ).
).
Введём в рассмотрение множества индексов активных ограничений
в
фиксированной точке
![]() :
:
![]() -
индексное множество активных нелинейных
ограничений;
-
индексное множество активных нелинейных
ограничений;
![]() - индексное
множество активных линейных ограничений;
- индексное
множество активных линейных ограничений;
![]() ;
;![]()
![]() .
.
Введем в рассмотрение
множество n-мерных
векторов
![]() в точке
в точке
![]() и построим множество
и построим множество
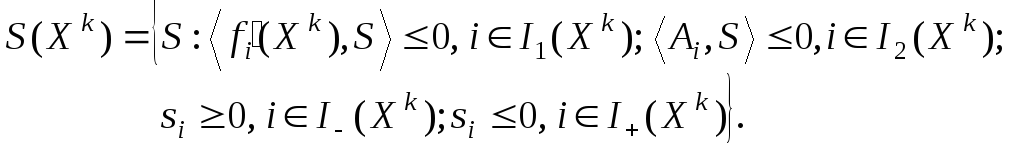
Множество
![]()
![]() представляет
собой конус
возможных направлений
в точке
представляет
собой конус
возможных направлений
в точке
![]() .
Если
.
Если
![]() - внутренняя точка множества R,
то множество
- внутренняя точка множества R,
то множество
![]() пусто, т.е. в этой точке
пусто, т.е. в этой точке
![]() нет активных ограничений, и на выбор
вектора S
не накладывается никаких ограничений.
нет активных ограничений, и на выбор
вектора S
не накладывается никаких ограничений.
Введем искусственную
переменную
![]() и определим
множество (n+1)-мерных
векторов
и определим
множество (n+1)-мерных
векторов
![]() следующим образом:
следующим образом:
![]()
![]()
![]() .
.
Задачу выбора подходящего направления сформулируем как задачу линейного программирования:
![]() .
(13.7)
.
(13.7)
Очевидно, что при
![]() множества
множества![]() и
и
![]() совпадают. Если
совпадают. Если
![]() ,
то из ограничения
,
то из ограничения
![]() следует,
что
следует,
что
![]() и направление
и направление
![]() будет подходящим. В этом случае
будет подходящим. В этом случае
![]() ,
т.е.
,
т.е.
![]() не направлено по касательной к нелинейным
границам. При этом, чем больше
не направлено по касательной к нелинейным
границам. При этом, чем больше
![]() ,
тем больше отличается от нуля
,
тем больше отличается от нуля
![]() ,
т.е. тем больший угол образуется между
,
т.е. тем больший угол образуется между
![]() и внешней нормалью
и внешней нормалью
![]() .
Если
.
Если![]() ,
то точка
,
то точка
![]() оказывается точкой минимума функции
оказывается точкой минимума функции
![]() .
.
Присутствие в
задаче (13.7) ограничения
![]() объясняется следующим образом. Когда
речь идёт о выборе направления, нас
интересует именно направление, которое
задаётся некоторым вектором произвольной
длины. Но при решении ЗЛП (13.7) величина
объясняется следующим образом. Когда
речь идёт о выборе направления, нас
интересует именно направление, которое
задаётся некоторым вектором произвольной
длины. Но при решении ЗЛП (13.7) величина
![]() может оказаться неограниченной. Чтобы
этого избежать следует наложить на
длину S
некоторые ограничения. Поэтому в
постановке задачи (13.7) должно присутствовать
так называемое условие
нормализации.
Таким условием может быть одно из
следующих ограничений:
может оказаться неограниченной. Чтобы
этого избежать следует наложить на
длину S
некоторые ограничения. Поэтому в
постановке задачи (13.7) должно присутствовать
так называемое условие
нормализации.
Таким условием может быть одно из
следующих ограничений:
№1.![]()
![]() .
.
№2.![]()
№3.![]() если
если
![]() или
или
![]() если
если
![]()
№4.![]()
Признак оптимальности в задаче выбора наилучшего подходящего направления устанавливается следующей теоремой.
Теорема 13.2.
Точка
![]() является точкой минимума
является точкой минимума
![]() на
на
![]() ,
регулярном по Слейтеру тогда и только
тогда, когда
,
регулярном по Слейтеру тогда и только
тогда, когда
![]() для всех
для всех
![]() ,
удовлетворяющих неравенству
,
удовлетворяющих неравенству
![]() .
.
Д о к а з а т е л ь
с т в о.Если в решении
![]() задачи выбора направления (13.7) окажется,
что
задачи выбора направления (13.7) окажется,
что
![]() ,
то соответствующее направление
,
то соответствующее направление
![]() будет подходящим, и точка
будет подходящим, и точка
![]() не может быть точкой минимума функции
не может быть точкой минимума функции
![]() .
.
Пусть теперь
![]() для всех
для всех
![]() ,
удовлетворяющих условиям
,
удовлетворяющих условиям
|
|
|
(13.8) |
|
|
(13.9) |
|
|
|
(13.10) |
Будем считать для
сокращения записей, что в (13.10) содержатся
также и прямые ограничения на переменные
задачи
![]() .
.
Введя в рассмотрение
![]() - мерные вектора
- мерные вектора
![]() ,
,
![]() неравенство
неравенство
![]() можно записать в виде
можно записать в виде
![]()
В силу теоремы Фаркаша, устанавливающей равносильность условий
![]() ,
,
найдется такой
вектор
![]() ,
,
![]() ,
что имеют место равенства
,
что имеют место равенства
|
|
(13.11) |
|
(13.12) |
Если
![]() ,
т.е.
,
т.е.
![]() ,
то из (13.11)
,
то из (13.11)
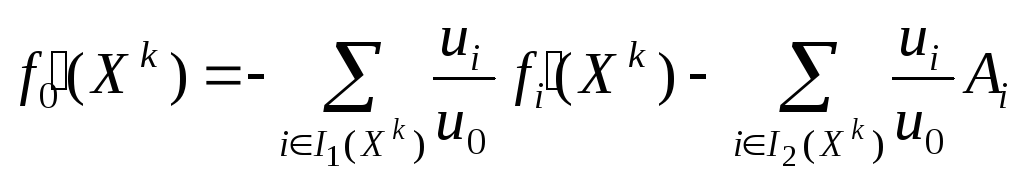 ,
(13.13)
,
(13.13)
Умножая скалярно
равенство (13.13) на некоторый произвольный
вектор
![]() ,
принадлежащий множеству
,
принадлежащий множеству
![]() получим
получим
 .
.
Но в множестве
![]() выполняются условия
выполняются условия
![]() и
и
![]() для любого
для любого
![]() .
Следовательно,
.
Следовательно,
![]() для любого
для любого
![]() ,
а значит в точке
,
а значит в точке
![]() нет подходящего направления и она
является точкой минимума функции
нет подходящего направления и она
является точкой минимума функции
![]() на
на
![]() .
.
Если
![]() ,
то из условия
,
то из условия
![]() и равенства (13.12) следует существование
по крайней мере одного
и равенства (13.12) следует существование
по крайней мере одного
![]() ,
,
![]() .
Тогда умножая (13.11) на
.
Тогда умножая (13.11) на
![]()
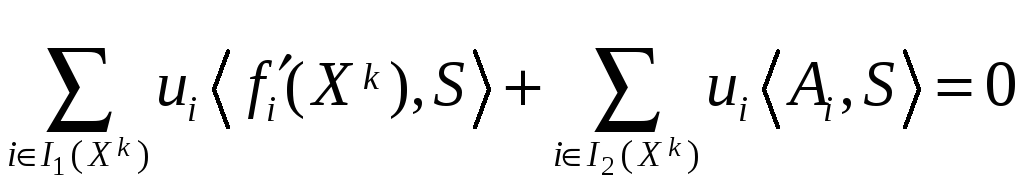 (13.14)
(13.14)
Но из регулярности
по Слейеру следует существование точки
![]() такой, что
такой, что
![]() для всех
для всех
![]() .
Тогда, полагая
.
Тогда, полагая
![]() ,
в силу теоремы 12.5 имеем
,
в силу теоремы 12.5 имеем
![]()
т.к.
![]() ,
а
,
а
![]() .
Таким образом, хотя бы одно из слагаемых
в (13.14) строго меньше нуля а все остальные
неположительны. Поэтому левая часть
равенства (13.14) не может быть равна нулю,
т.е. случай
.
Таким образом, хотя бы одно из слагаемых
в (13.14) строго меньше нуля а все остальные
неположительны. Поэтому левая часть
равенства (13.14) не может быть равна нулю,
т.е. случай
![]() невозможен. Теорема доказана.
невозможен. Теорема доказана.