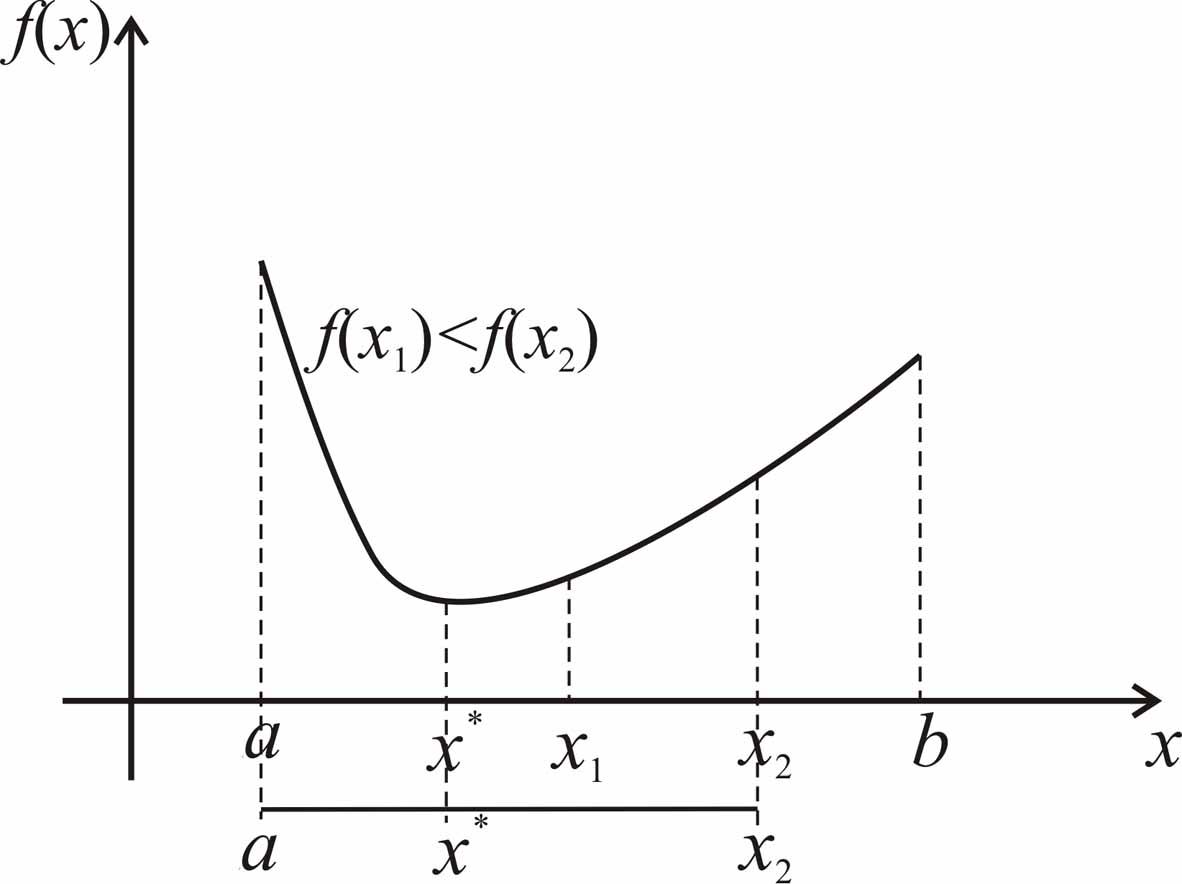
Методы исключения отрезков

В методе перебора, рассмотренном выше, точки , в которых определяются значения , выбираются заранее. Если же для выбора очередной точки вычисления (измерения) использовать информацию, содержащуюся в уже найденных значениях , то поиск точки минимума можно сделать более эффективным, т.е. сократить число определяемых для этого значений ), как, например, в методе поразрядного поиска.

Один из путей такого более эффективного поиска точки указывает свойство 3 унимодальных функций.

Пусть . Сравнив значения в точках и (пробных точках), можно сократить отрезок поиска точки , перейдя к отрезку , если , или к отрезку , если (рис. 3.2). Описанную процедуру можно повторить необходимое число раз, последовательно уменьшая отрезок, содержащий точку минимума. Когда длина последнего из найденных отрезков станет достаточно малой, следует положить , где - одна из точек этого отрезка, например, его середина. Методы минимизации, основанные на этом принципе, называются методами исключения отрезков.

Рис. 3.2. Уменьшение отрезка поиска точки минимума методами исключения отрезков

Чтобы относительное уменьшение отрезка на каждой итерации не зависело от того, какая из его частей исключается из дальнейшего рассмотрения, пробные точки следует располагать симметрично относительно середины исходного отрезка. В зависимости от способа выбора пробных точек получаются различные методы исключения отрезков. На практике используются следующие.

Метод деления отрезка пополам (дихотомии)

В этом методе точки и располагаются близко к середине очередного отрезка , т.е.

, , (3.3)

где - малое число. При этом отношение длин нового и исходного отрезков близко к 1/2, этим и объясняется название метода.

Отметим, что для любых точек и величина , поэтому указанный выбор пробных точек объясняется стремлением обеспечить максимально возможное относительное уменьшение отрезка на каждой итерации поиска .

В конце вычислений по методу дихотомии в качестве приближенного значения берут середину последнего из найденных отрезков , убедившись предварительно, что достигнуто неравенство .

Опишем алгоритм метода деления отрезка пополам.

Шаг 1. Определить и по формулам (3.3). Вычислить и .

Шаг 2. Сравнить и . Если , то перейти к отрезку , положив , иначе - к отрезку , положив .

Шаг 3. Найти достигнутую точность . Если , то перейти к следующей итерации, вернувшись к шагу 1. Если , то завершить поиск , перейдя к шагу 4.

Шаг 4. Положить , .

Замечание 1. Число из (3.3) выбирается на интервале (0;2) с учетом следующих соображений:

а) чем меньше , тем больше относительное уменьшение длины отрезка на каждой итерации, т.е. при уменьшении достигается более высокая скорость сходимости метода дихотомии;

б) при чрезмерно малом сравнение значений в точках и отличающихся на величину , становится затруднительным. Поэтому выбор должен быть согласован с точностью определения и с количеством верных десятичных знаков при задании аргумента х.

Замечание 2. Число итераций метода дихотомии, необходимое для определения точки с точностью , определяется неравенством

(3.4)

В самом деле, обозначим длину исходного отрезка через . Длина отрезка, полученного после первой итерации, будет

,

после второй итерации

,

после третьей

и т.д.

Таким образом, в результате итераций длина отрезка поиска точки станет .

При этом будет достигнута точность определения точки минимума . Находя из условия

(3.5)

получаем неравенство (3.4)

Замечание 3. Величина может быть выбрана достаточно малой, поэтому, пренебрегая ею в (3.4), получаем: . На каждой итерации метода дихотомии вычисляются два значения . Поэтому после вычислений производится итераций и достигается точность определения :

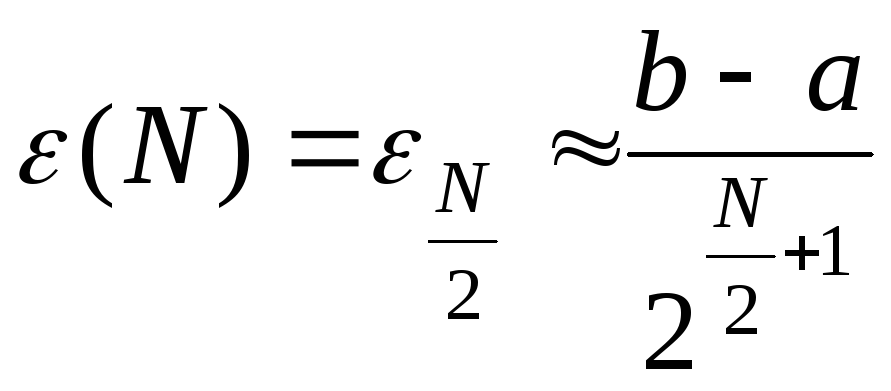(3.6)

Метод золотого сечения

Рассмотрим такое симметричное расположение точек и на отрезке , при котором одна из них становится пробной точкой и на новом отрезке, полученном после исключения части исходного отрезка. Использование таких точек позволяет на каждой итерации метода исключения отрезков, кроме первой, ограничиться определением только одного значения , так как другое значение уже найдено на одной из предыдущих итераций.

Найдем точки и , обладающие указанным свойством.

Рассмотрим сначала отрезок и для определенности предположим, что при его уменьшении исключается правая часть этого отрезка. Пусть , тогда симметрично расположенная точка (рис. 3.3).

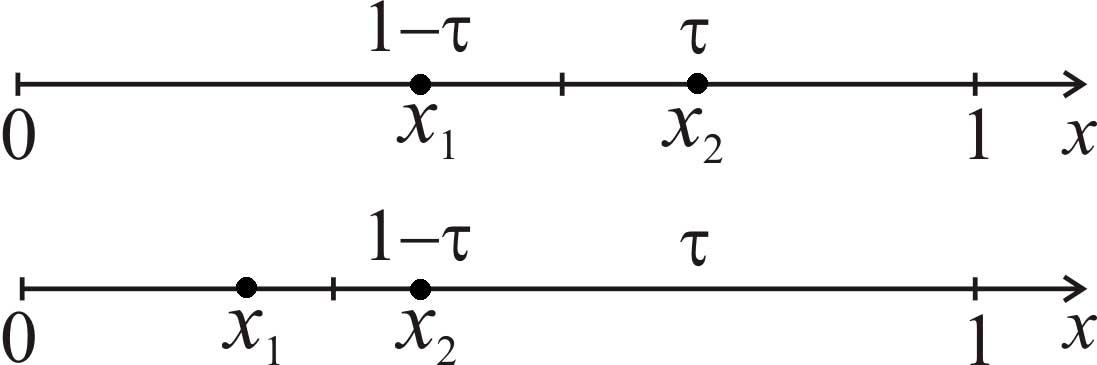
Рис. 3.3. К определению пробных точек в методе золотого сечения

Пробная точка отрезка перейдет в пробную точку нового отрезка . Чтобы точки и делили отрезки и в одном и том же отношении, должно выполняться равенство или , откуда находим положительное значение …. Таким образом, , .

Для произвольного отрезка выражения для пробных точек примут вид

(3.7)

Точки и из (3.7) обладают следующим свойством: каждая из них делит отрезок на две неравные части так, что отношение длины всего отрезка к длине его большей части равно отношению длин большей и меньше частей отрезка. Точки с таким свойством называются точками золотого сечения отрезка . Это и объясняет название рассматриваемого метода.

На каждой итерации исключения отрезков с пробными точками (3.7) одна из них переходит на следующий отрезок и значение в этой точке вычислять не следует. Если новым отрезком становится , то на него переходит пробная точка исходного отрезка, становясь его второй пробной точкой (рис. 3.3). В случае перехода к отрезку пробная точка исходного отрезка становится первой пробной точкой отрезка .

Легко проверить, что . Поэтому на каждой итерации метода золотого сечения недостающую пробную точку нового отрезка можно найти по перешедшей на него пробной точке с помощью сложения и вычитания, не используя формул (3.7).

В конце вычислений по методу золотого сечения в качестве приближенного значения можно взять середину последнего из полученных отрезков .

На каждой итерации отрезок поиска точки минимума уменьшается в одном и том же отношении , поэтому в результате итераций его длина становится . Таким образом, точность , определения точки после итераций находится из равенства

, (3.8)

а условием окончания поиска точки с точностью е служит неравенство .

Опишем алгоритм метода золотого сечения.

Шаг 1. Найти и по формулам (3.7). Вычислить и . Положить , .

Шаг 2. Проверка на окончание поиска: если , то перейти к шагу 3, иначе — к шагу 4.

Шаг 3. Переход к новому отрезку и новым пробным точкам. Если , то положить , , , и вычислить , иначе - пожить , , , и вычислить . Положить и перейти к шагу 2.

Шаг 4. Окончание поиска: положить ,

Замечание. Число итераций, необходимое для достижения заданной точности , можно найти из условия с учетом соотношения (3.8):

.

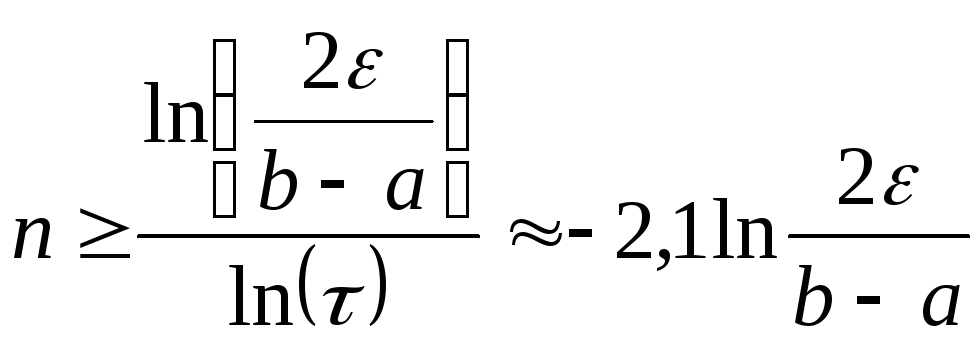Так как вычислений позволяют выполнить итераций метода золотого сечения, то достигнутая в результате этих вычислений точность определения составляет

.

Эффективность прямых методов обычно оценивают или по объему вычислений, обеспечивающему заданную точность, или по гарантированной точности, достигнутой в результате выполнения заданного объема вычислений. Поскольку при реализации методов перебора определение значений функции требует несравненно больших затрат, чем выполнение таких вспомогательных операций, как вычисление точек перебора, сравнение значений функции и т.п., то объем вычислений можно оценить количеством N вычислений значений функции .

Метод считается тем эффективнее, чем меньше , гарантирующее заданную точность определения точки минимума функции . Для сравнения рассматриваемых методов по этому признаку рекомендуется составить таблицу значений в зависимости от требуемой точности определения .

При сравнении методов по точности более эффективным считается тот из рассматриваемых методов, который обеспечивает достижение меньшего значения при одинаковом объеме вычислений. Для получения вывода о точности рекомендуется составить таблицу значений достигнутой точности в зависимости от количества найденных значений функции для анализируемых методов.