Лекция №2
Методы одномерной оптимизации
Изложение методов оптимизации начнем с рассмотрения простейшей математической модели оптимизации, в которой целевая функция зависит от одной переменной. Такие задачи возникают при изучении объектов, зависящих от одной скалярной переменной, когда требуется выбрать эту переменную наилучшим в том или ином смысле образом. Кроме того, эти задачи входят как составная часть во многие итерационные методы решения задач минимизации функций многих переменных и других более сложных экстремальных задач.
С задачами минимизации функций одной переменной мы впервые сталкиваемся при изучении начальных глав математического анализа и решаем их методами дифференциального исчисления. Может показаться, что задачи минимизации функций одной переменной достаточной просты и методы их решения хорошо разработаны и изучены. Однако это не совсем так. Оказалось, что методы дифференциального исчисления находят ограниченное применение и далеко не всегда удобны для реализации в компьютерных программах. Хотя в последнее время и появились другие, более удобные для реализации, методы, но, тем не менее, эту область экстремальных задач нельзя считать завершенной. Мы остановимся на некоторых наиболее известных методах, достаточно хорошо проявивших себя на практике.
Постановка задачи одномерной оптимизации
Пусть функция
![]() определена на некотором множестве U
вещественной оси
определена на некотором множестве U
вещественной оси
![]() .
Поскольку максимизация целевой функции
.
Поскольку максимизация целевой функции
![]() эквивалентна минимизации противоположной
величины
эквивалентна минимизации противоположной
величины
![]() ,
будем рассматривать только задачу
минимизации функции
,
будем рассматривать только задачу
минимизации функции
![]() на множестве U.
Начнем с того, что уточним постановку
этой задачи. Для этого напомним некоторые
основные понятия.
на множестве U.
Начнем с того, что уточним постановку
этой задачи. Для этого напомним некоторые
основные понятия.
Определение 2.1.
Число
![]() называется точкой
глобального (абсолютного) минимума
или просто точкой
минимума
функции
называется точкой
глобального (абсолютного) минимума
или просто точкой
минимума
функции
![]() на множестве U,
если
на множестве U,
если
![]() для всех
для всех
![]() .
Значение
.
Значение
![]() называется глобальным
(абсолютным)
минимумом
или просто минимумом
функции
называется глобальным
(абсолютным)
минимумом
или просто минимумом
функции
![]() на U.
Множество всех точек минимума функции
на U.
Множество всех точек минимума функции
![]() на U
будем обозначать через
на U
будем обозначать через
![]() .
.
Определение 2.2.
Число
![]() называется точкой
локального минимума
функции
называется точкой
локального минимума
функции
![]() на U,
если
на U,
если
![]() для всех
для всех
![]() ,
достаточно близких к
,
достаточно близких к
![]() ,
т.е. если существует число
,
т.е. если существует число
![]() такое, что это неравенство выполняется
для любого
такое, что это неравенство выполняется
для любого
![]() .
.
В зависимости от
свойств множества U
и функции
![]() множество
множество
![]() может содержать одну, несколько или
даже бесконечно много точек. Также
возможны случаи, когда
может содержать одну, несколько или
даже бесконечно много точек. Также
возможны случаи, когда
![]() пусто.
пусто.
Пример 2.1.
Пусть
![]() при
при
![]() и
и
![]() .
На множестве
.
На множестве
![]() минимальное значение
минимальное значение
![]() равно нулю, а множество
равно нулю, а множество
![]() состоит из единственной точки
состоит из единственной точки
![]() .
Если
.
Если
![]() ,
то
,
то
![]() содержит три точки
содержит три точки
![]() ,
1. В случае
,
1. В случае
![]() функция
функция
![]() не имеет наименьшего значения на U.
В самом деле, какую бы точку
не имеет наименьшего значения на U.
В самом деле, какую бы точку
![]() мы не взяли, найдется точка из U
такая, что значение в ней будет меньше
мы не взяли, найдется точка из U
такая, что значение в ней будет меньше
![]() .
Это значит, что
.
Это значит, что
![]() пусто.
пусто.
Пример 2.2.
Пусть
![]() .
Минимальное значение
.
Минимальное значение
![]() на U
равно нулю, множество
на U
равно нулю, множество
![]() состоит из единственной точки.
состоит из единственной точки.
Пример 2.3.
Пусть
![]() .
Здесь
.
Здесь
![]() ,
т.к. во всех точках из U
функция принимает конечные значения,
а для последовательности
,
т.к. во всех точках из U
функция принимает конечные значения,
а для последовательности
![]() имеем
имеем
![]() .
.
В примерах 2.1–2.2 функции ограничены снизу на рассматриваемых множествах, а в примере 2.3 функция не ограничена снизу.
Определение 2.3.
Функция
![]() называется ограниченной
снизу на
множестве U,
если существует число M
такое, что
называется ограниченной
снизу на
множестве U,
если существует число M
такое, что
![]() для всех
для всех
![]() .
.
В тех случаях,
когда
![]() ,
естественным обобщением понятия
наименьшего значения функции является
понятие нижней грани функции.
,
естественным обобщением понятия
наименьшего значения функции является
понятие нижней грани функции.
Определение 2.4.
Пусть функция
![]() ограничена снизу на множестве U.
Тогда число
ограничена снизу на множестве U.
Тогда число
![]() называется точной
нижней гранью
функции
называется точной
нижней гранью
функции
![]() на множестве U,
если 1)
на множестве U,
если 1)
![]() при всех
при всех
![]() ;
2) для любого сколь угодно малого числа
;
2) для любого сколь угодно малого числа
![]() найдется точка
найдется точка
![]() такая, что
такая, что
![]() .
.
Если функция
![]() неограниченна снизу на U,
то в качестве нижней грани
неограниченна снизу на U,
то в качестве нижней грани
![]() на U
принимается
на U
принимается
![]() .
Точную нижнюю грань
.
Точную нижнюю грань
![]() на U
обозначают через
на U
обозначают через
![]() .
.
В примерах 2.1–2.2
нижняя грань
![]() ,
а в примере 2.3
,
а в примере 2.3
![]() .
.
Если
![]() ,
то, очевидно, нижняя грань
,
то, очевидно, нижняя грань
![]() на U
совпадает с наименьшим значением
на U
совпадает с наименьшим значением
![]() этой функции на U,
т.е.
этой функции на U,
т.е.
![]() .
В этом случае говорят, что функция
.
В этом случае говорят, что функция
![]() на U
достигает своей нижней грани. Отметим,
что
на U
достигает своей нижней грани. Отметим,
что
![]() всегда существует, а
всегда существует, а
![]() ,
как видно из примеров 2.1–2.3 не всегда
имеет смысл.
,
как видно из примеров 2.1–2.3 не всегда
имеет смысл.
Пример 2.4.
Пусть
![]() .
Покажем, что функция
.
Покажем, что функция
![]() на U
не имеет точек минимума, а точная нижняя
грань существует.
на U
не имеет точек минимума, а точная нижняя
грань существует.
Предположим,
![]() ,
т.е. существует хотя бы одна точка
,
т.е. существует хотя бы одна точка
![]() такая, что
такая, что
![]() для всех
для всех
![]() .
Выберем произвольное число
.
Выберем произвольное число
![]() .
Очевидно
.
Очевидно
![]() ,
причем
,
причем
![]() ,
что противоречит предыдущему неравенству.
Поэтому исходное предположение неверно
и
,
что противоречит предыдущему неравенству.
Поэтому исходное предположение неверно
и
![]() .
.
Убедимся в том,
что число 0 является точной нижней гранью
данной функции
![]() на U.
В самом деле, для всех
на U.
В самом деле, для всех
![]() имеем
имеем
![]() ,
т.е. число 0 удовлетворяет первому из
неравенств в определении 2.4. Далее пусть
,
т.е. число 0 удовлетворяет первому из
неравенств в определении 2.4. Далее пусть
![]() .
Возьмем произвольное
.
Возьмем произвольное
![]() .
Тогда, очевидно,
.
Тогда, очевидно,
![]() и
и
![]() ,
т.е. для числа 0 выполняется и второе
неравенство из определения точной
нижней грани. Поэтому
,
т.е. для числа 0 выполняется и второе
неравенство из определения точной
нижней грани. Поэтому
![]() .
.
Если множество
точек минимума функции
![]() на U
пусто, то задача минимизации
на U
пусто, то задача минимизации
![]() теряет смысл. В этом случае можно
ограничиться поиском точки
теряет смысл. В этом случае можно
ограничиться поиском точки
![]() ,
в которой значение
,
в которой значение
![]() с заданной погрешностью ε
приближает точную нижнюю грань функции
с заданной погрешностью ε
приближает точную нижнюю грань функции
![]() на множестве U,
т.е.
на множестве U,
т.е.
![]() .
.
Определение 2.5.
Последовательность точек
![]() из U
называется минимизирующей
последовательностью
для функции
из U
называется минимизирующей
последовательностью
для функции
![]() на множестве U,
если
на множестве U,
если
![]() .
.
Из определения и существования точной нижней грани следует, что минимизирующая последовательность всегда существует.
Теперь можем
перейти к формулировке постановки
задачи одномерной оптимизации как
задачи минимизации функции
![]() на множестве U.
на множестве U.
Условимся, что запись
|
|
(2.1) |
или, ей эквивалентная
![]() будет означать, что ставится задача
определения величины
будет означать, что ставится задача
определения величины
![]() .
Причем в задаче (2.1) неважно, будет ли
множество
.
Причем в задаче (2.1) неважно, будет ли
множество
![]() точек минимума
точек минимума
![]() на U
непустым, или оно пусто. В случае, когда
множество
на U
непустым, или оно пусто. В случае, когда
множество
![]() непусто, требуется наряду с
непусто, требуется наряду с
![]() найти точку
найти точку
![]() .
.
Заметим, что
получить точное решение поставленной
задачи (2.1) удается лишь в редких случаях.
Поэтому на практике при решении задачи
(2.1) обычно строят минимизирующую
последовательность
![]() для функции
для функции
![]() на U
и затем в качестве приближения для
на U
и затем в качестве приближения для
![]() берут величину
берут величину
![]() при достаточно большом k.
В случае непустого множества
при достаточно большом k.
В случае непустого множества
![]() достаточно построить минимизирующую
последовательность
достаточно построить минимизирующую
последовательность
![]() ,
которая сходится к множеству
,
которая сходится к множеству
![]() .
Один достаточно широкий класс функций,
для которых
.
Один достаточно широкий класс функций,
для которых
![]() ,
определяет известная теорема Вейерштрасса,
согласно которой функция, непрерывная
на замкнутом ограниченном множестве,
достигает на этом множестве своих
максимального и минимального значений.
Таким образом, задача (2.1) с непрерывной
целевой функцией
,
определяет известная теорема Вейерштрасса,
согласно которой функция, непрерывная
на замкнутом ограниченном множестве,
достигает на этом множестве своих
максимального и минимального значений.
Таким образом, задача (2.1) с непрерывной
целевой функцией
![]() на U
всегда имеет решение.
на U
всегда имеет решение.
Если функция
![]() на множестве U
имеет, кроме глобального, локальные
минимумы, отличные от него, то минимизация
на множестве U
имеет, кроме глобального, локальные
минимумы, отличные от него, то минимизация
![]() ,
как правило, сильно затрудняется. Многие
методы поиска точки минимума
,
как правило, сильно затрудняется. Многие
методы поиска точки минимума
![]() приспособлены только для функций, у
которых каждый локальный минимум
является одновременно и глобальным.
Этим свойством обладают унимодальные
функции.
приспособлены только для функций, у
которых каждый локальный минимум
является одновременно и глобальным.
Этим свойством обладают унимодальные
функции.
Унимодальные функции
Определение 2.6.
Функция
![]() называется унимодальной
на отрезке
называется унимодальной
на отрезке
![]() ,
если она непрерывна на
,
если она непрерывна на
![]() и существуют числа α,
β:
и существуют числа α,
β:
![]() такие, что
такие, что
1)
![]() монотонно убывает при
монотонно убывает при
![]() (если
(если
![]() );
);
2)
![]() монотонно возрастает при
монотонно возрастает при
![]() (если
(если
![]() );
);
3)
![]() при
при
![]() ,
так что
,
так что
![]() .
.
Множество
унимодальных на отрезке
![]() функций мы
будем обозначать через
функций мы
будем обозначать через
![]() .
.
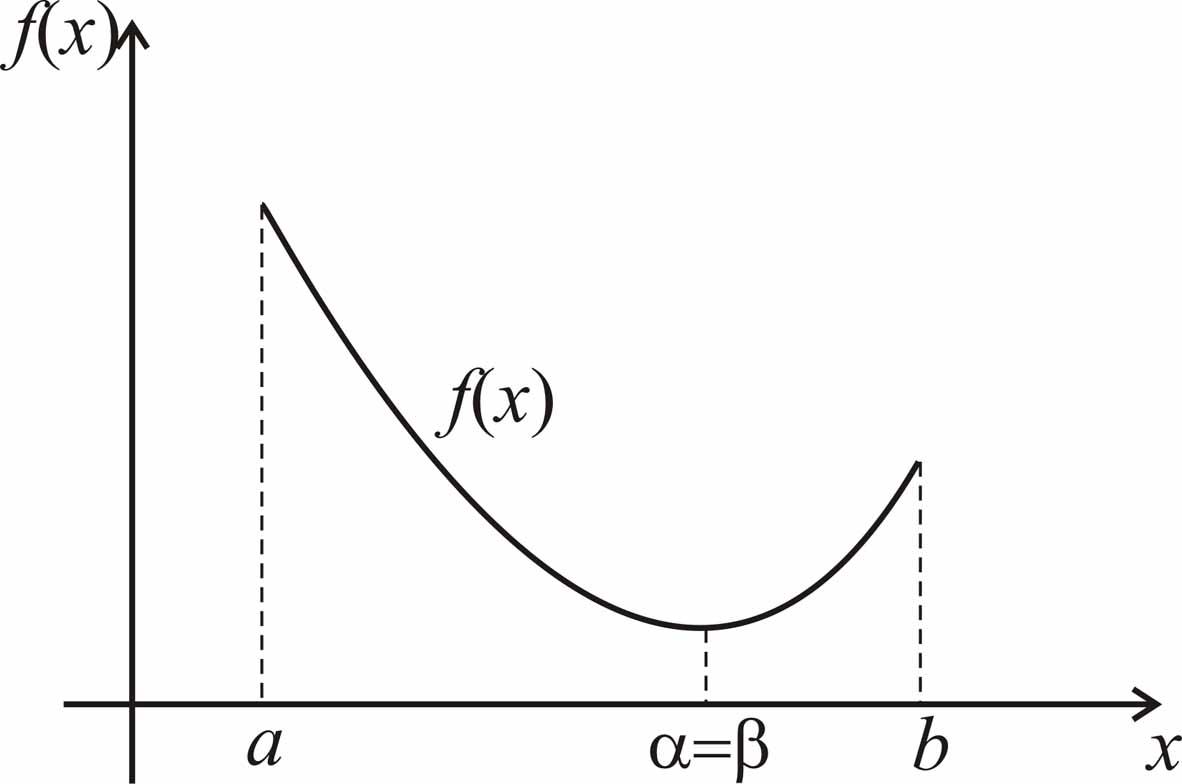
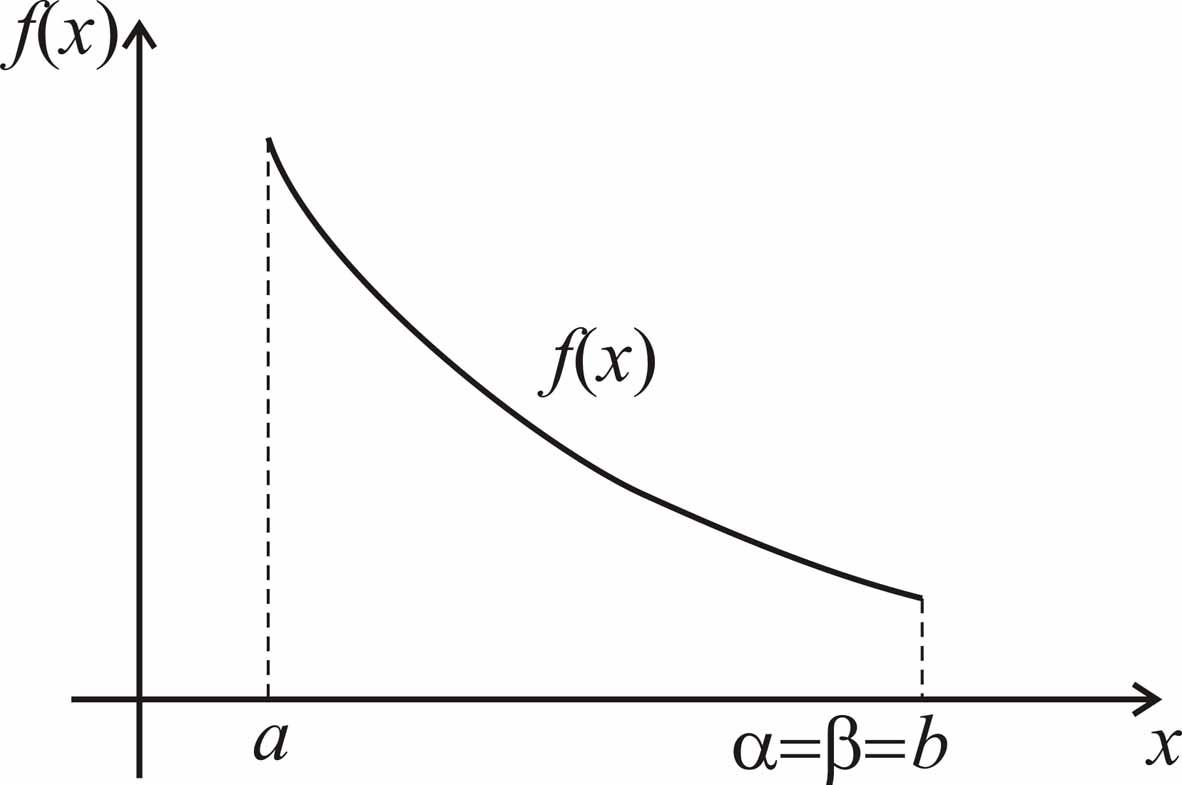
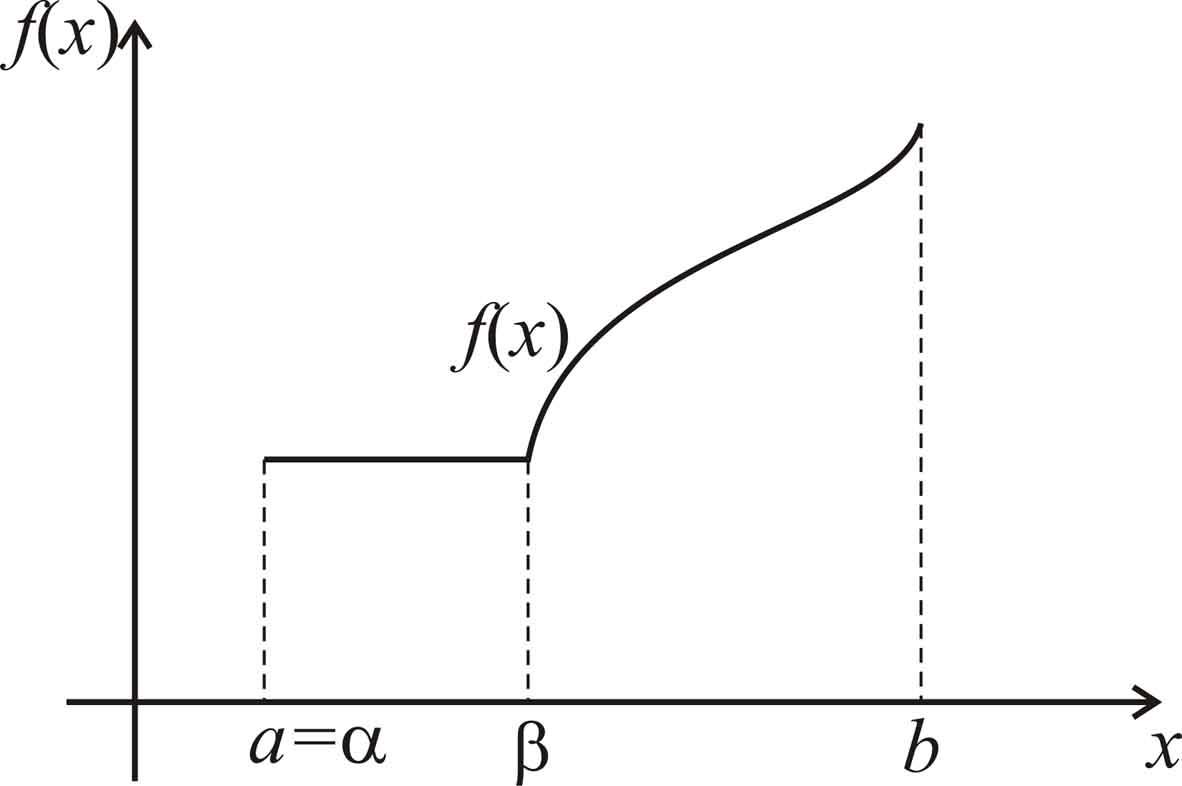
Отметим, что
возможно вырождение в точку одного или
двух отрезков из
![]() ,
,
![]() и
и
![]() .
Некоторые варианты расположения и
вырождения в точку отрезков монотонности
и постоянства унимодальной функции
показаны на рис. 2.1.
.
Некоторые варианты расположения и
вырождения в точку отрезков монотонности
и постоянства унимодальной функции
показаны на рис. 2.1.
|
|
|
|
|
|
|
Рис. 2.1. Графики унимодальных функций. |
|
Из определения 2.6 вытекают следующие основные свойства унимодальных функций.
-
Любая из точек локального минимума унимодальной функции является и точкой ее глобального минимума на отрезке
 .
. -
Функция, унимодальная на отрезке
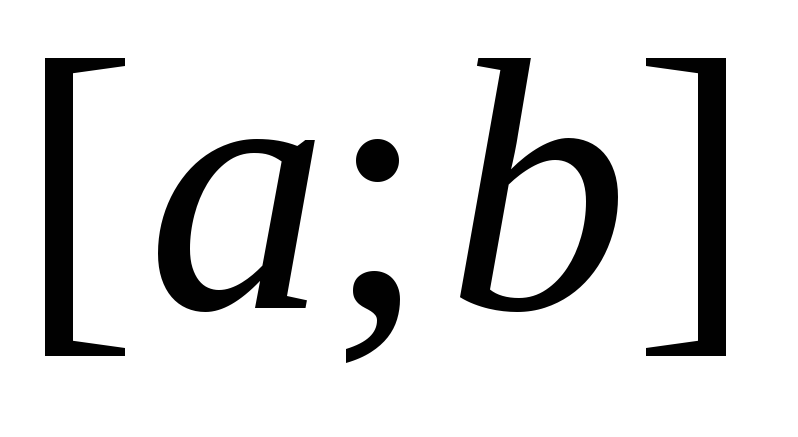 ,
является
унимодальной и на любом меньшем отрезке
,
является
унимодальной и на любом меньшем отрезке
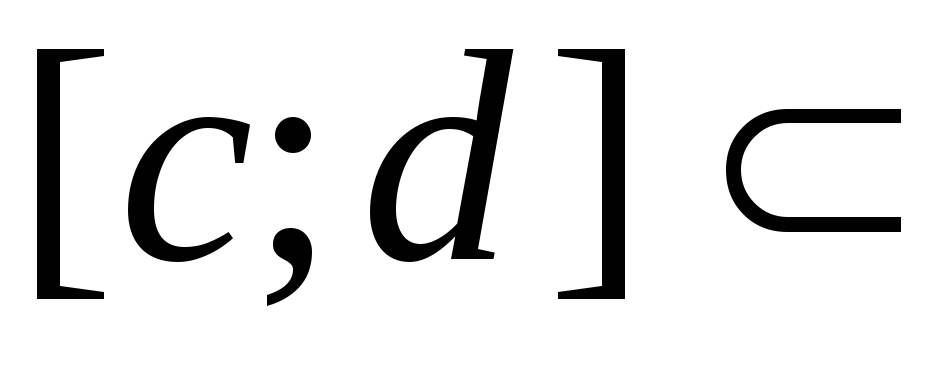
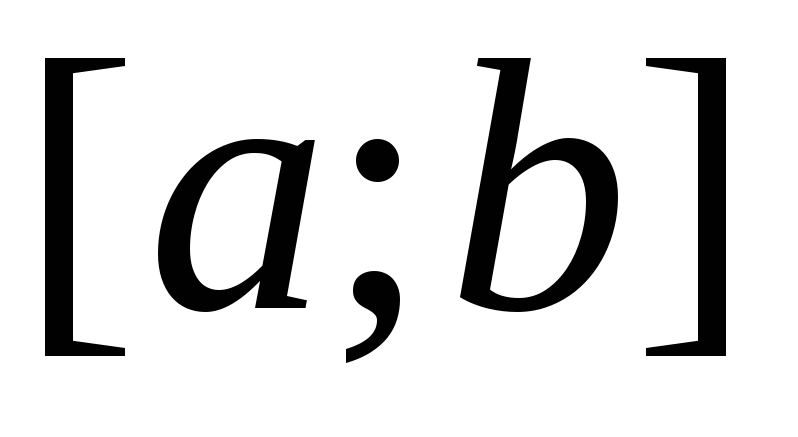 .
. -
Пусть
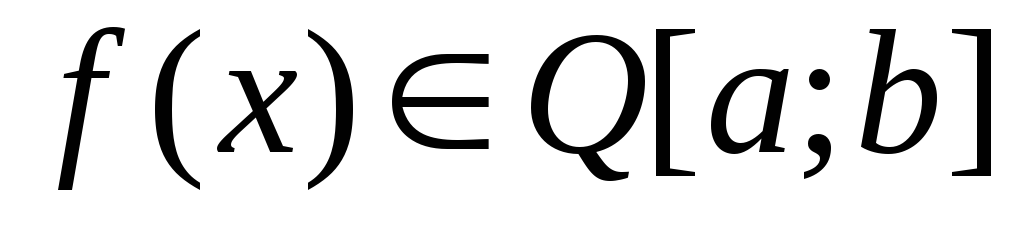 и
и
 .
Тогда:
.
Тогда:
|
если
если
|
(2.2) |
где
![]() - одна из точек минимума
- одна из точек минимума
![]() на отрезке
на отрезке
![]() .
.
Выпуклые функции
Определение 2.7.
Функция
![]() ,
заданная на отрезке
,
заданная на отрезке
![]() ,
называется
выпуклой на
этом отрезке, если для всех
,
называется
выпуклой на
этом отрезке, если для всех
![]() ,
,
![]() и произвольного
числа
и произвольного
числа
![]() выполняется неравенство
выполняется неравенство
![]() .
(2.3)
.
(2.3)
Перечислим основные свойства выпуклых функций.
1. Если функция
![]() выпукла на
выпукла на
![]() ,
то на любом
отрезке
,
то на любом
отрезке
![]() ее график
расположен не выше хорды, проведенной
через точки графика с абсциссами
ее график
расположен не выше хорды, проведенной
через точки графика с абсциссами
![]() и
и
![]() (рис. 2.2).
(рис. 2.2).
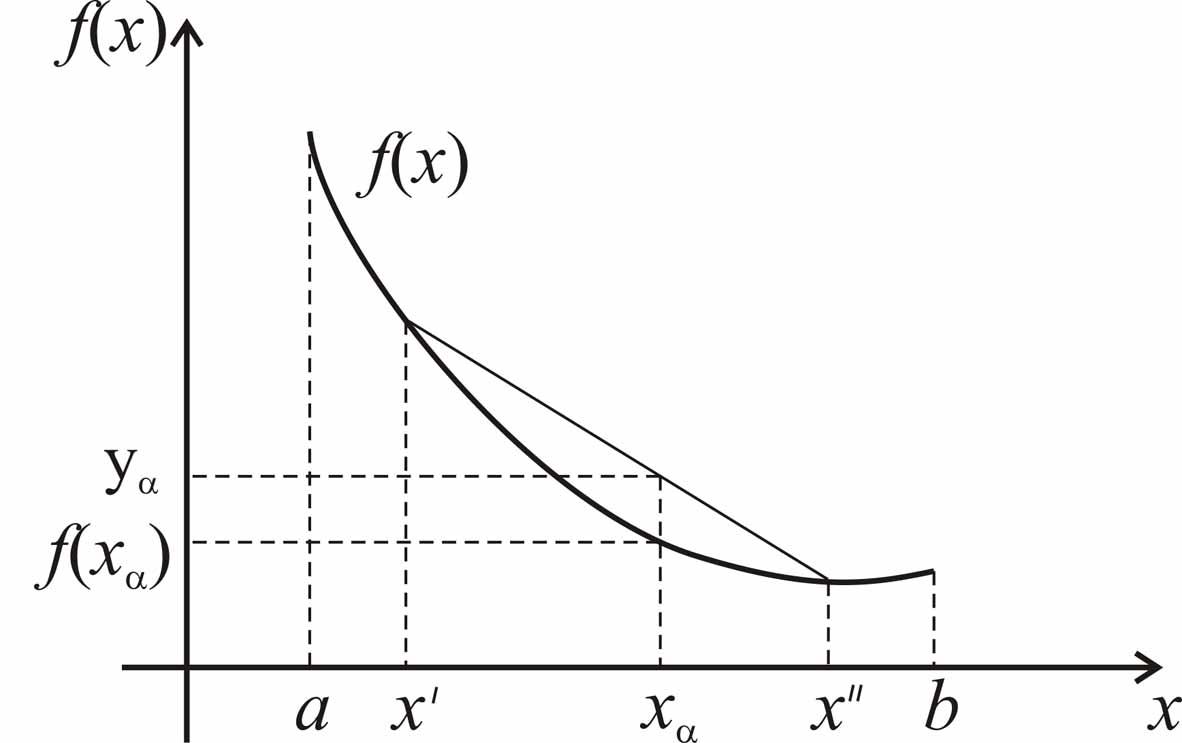
Рис. 2.2. Взаимное расположение графика выпуклой функции и хорды
Из курса математического анализа известны следующие условия выпуклости функции:
2.
Для того
чтобы дифференцируемая на отрезке
![]() функция
функция
![]() была выпуклой на этом отрезке, необходимо
и достаточно, чтобы производная
была выпуклой на этом отрезке, необходимо
и достаточно, чтобы производная
![]() не убывала на
не убывала на
![]() ;
;
3.
Для того чтобы дважды дифференцируемая
на отрезке
![]() функция
функция
![]() была
выпуклой на этом отрезке, необходимо и
достаточно, чтобы при всех
была
выпуклой на этом отрезке, необходимо и
достаточно, чтобы при всех
![]() выполнялось
неравенство
выполнялось
неравенство
![]() .
.
4. Условие выпуклости
для дифференцируемой на отрезке
![]() функции
функции
![]() означает, что на этом отрезке любая
касательная к графику
означает, что на этом отрезке любая
касательная к графику
![]() лежит не выше этого графика (рис. 2.3).
лежит не выше этого графика (рис. 2.3).
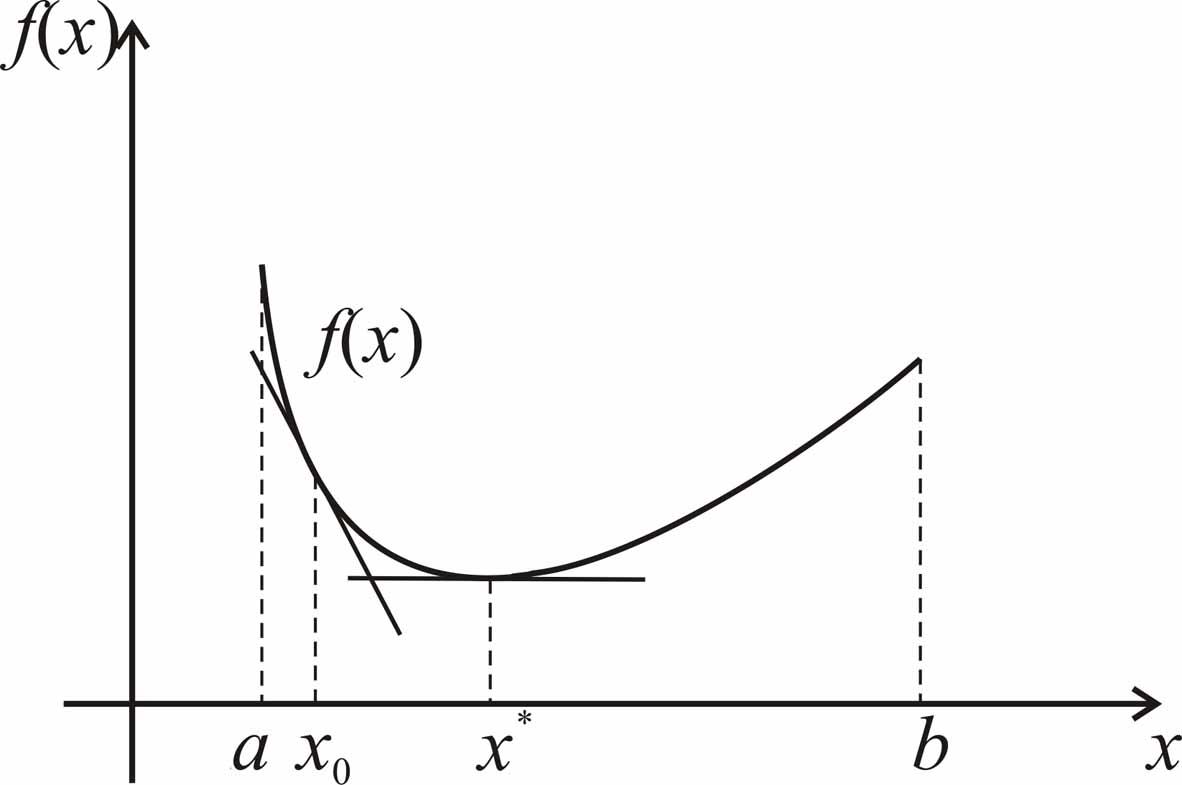
Рис. 2.3. Взаимное расположение графика выпуклой дифференцируемой
функции и касательной к нему
5. Если
![]() - выпуклая
дифференцируемая на отрезке
- выпуклая
дифференцируемая на отрезке
![]() функция и в точке
функция и в точке
![]() выполняется
равенство
выполняется
равенство
![]() ,
(2.4)
,
(2.4)
то
![]() является точкой глобального минимума
является точкой глобального минимума
![]() на
на
![]() .
.
Благодаря свойству
4 выпуклых функций данное свойство
приобретает простой геометрический
смысл: поскольку касательная к графику
![]() в точке с
абсциссой
в точке с
абсциссой
![]() горизонтальна,
а этот график расположен не ниже
касательной, то
горизонтальна,
а этот график расположен не ниже
касательной, то
![]() есть точка минимума
есть точка минимума
![]() (рис. 2.3).
(рис. 2.3).
Таким образом, равенство (2.4) для выпуклой дифференцируемой функции является не только необходимым условием глобального минимума (как для всякой дифференцируемой функции), но и его достаточным условием.
Замечание 1.
Можно показать, что всякая выпуклая
непрерывная на отрезке
![]() функция
является и унимодальной на этом отрезке.
Обратное, вообще говоря, неверно (рис.
2.4).
функция
является и унимодальной на этом отрезке.
Обратное, вообще говоря, неверно (рис.
2.4).
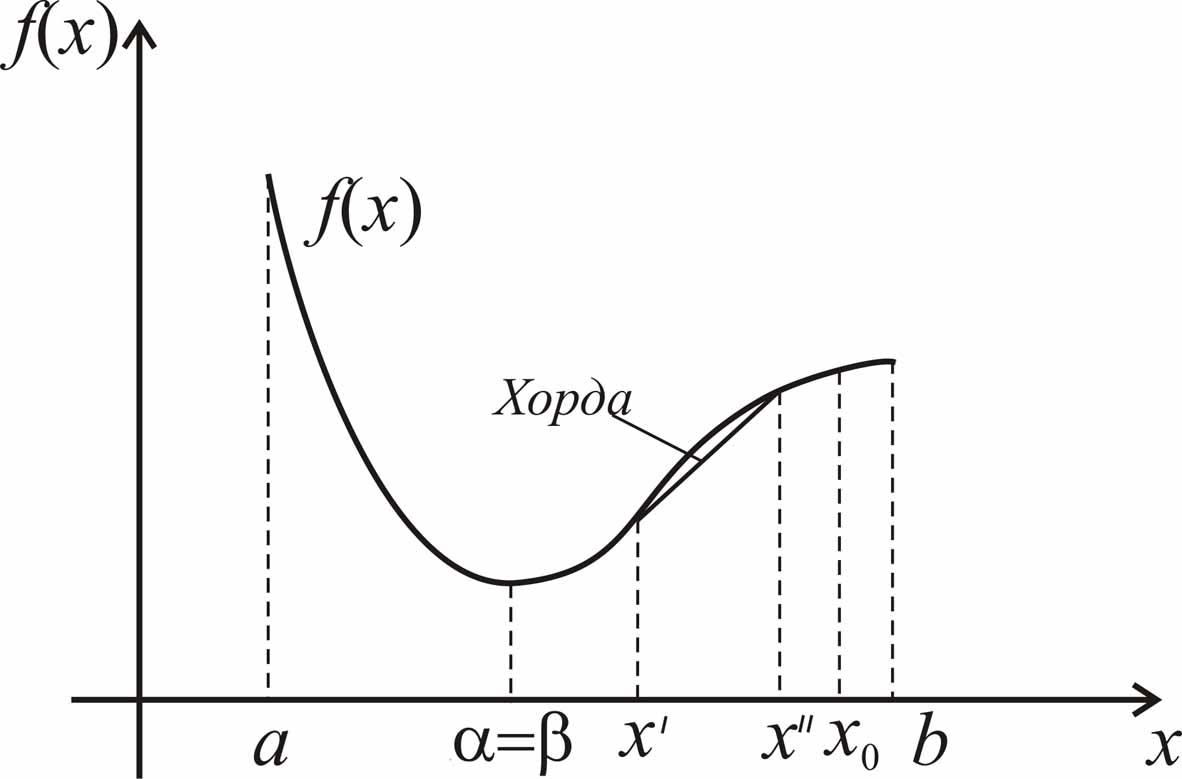
Рис. 2.4. График унимодальной, но не выпуклой функции
Таким образом, кроме перечисленных свойств, выпуклые функции обладают также и всеми свойствами унимодальных функции.
Замечание 2. При исследовании выпуклости функций на практике неравенство (2.3) удается использовать только в редких случаях. Поэтому для дифференцируемых достаточное число раз функций обычно применяют дифференциальные критерии выпуклости (см. свойства 2 и 3 выпуклых функций).
Замечание 3. Непосредственная проверка унимодальности с помощью определения 2.6 также в большинстве случаев вызывает затруднения, и для обоснования унимодальности достаточно гладких функций часто используют те же дифференциальные критерии выпуклости (свойства 2 и 3). Если функция оказывается выпуклой, то можно утверждать (замечание 1), что она унимодальна. Разумеется, при отрицательном результате проверки функции на выпуклость нельзя сделать вывод о том, что она не унимодальна.
Липшицевы функции
Применение некоторых
методов одномерной минимизации возможно
только в случае, если скорость изменения
целевой функции
![]() на любом
участке отрезка
на любом
участке отрезка
![]() ограничена
некоторым числом, одним и тем же для
всех участков. В этом случае говорят,
что
ограничена
некоторым числом, одним и тем же для
всех участков. В этом случае говорят,
что
![]() удовлетворяет на
удовлетворяет на
![]() условию
Липшица.
Целевые
функции большинства практических задач
оптимизации указанным свойством
обладают.
условию
Липшица.
Целевые
функции большинства практических задач
оптимизации указанным свойством
обладают.
Определение 2.8.
Функция
![]() удовлетворяет на отрезке
удовлетворяет на отрезке
![]() условию
Липшица, если существует такое число
условию
Липшица, если существует такое число
![]() (константа Липшица), что
(константа Липшица), что
![]() (2.5)
(2.5)
для всех
![]() и
и
![]() ,
принадлежащих
,
принадлежащих
![]() .
.
Липшицевы функции, т.е. функции удовлетворяющие условию (2.5) обладают рядом свойств.
1.
Если
неравенство (2.5) выполняется с константой
![]() ,
то оно
справедливо и при всех
,
то оно
справедливо и при всех
![]() .
Поэтому для
функции, удовлетворяющей условию
Липшица, существует бесконечное множество
констант
.
Поэтому для
функции, удовлетворяющей условию
Липшица, существует бесконечное множество
констант
![]() из (2.5).
из (2.5).
При использовании
алгоритмов минимизации, включающих
![]() как параметр,
наилучшие результаты достигаются, как
правило, если в качестве
как параметр,
наилучшие результаты достигаются, как
правило, если в качестве
![]() берется
минимальная из констант Липшица.
берется
минимальная из констант Липшица.
2.
Из условия
(2.5) непосредственно следует непрерывность
![]() на отрезке
на отрезке
![]() .
Поэтому,
согласно теореме Вейерштрасса, функция
.
Поэтому,
согласно теореме Вейерштрасса, функция
![]() ,
удовлетворяющая на отрезке
,
удовлетворяющая на отрезке
![]() условию
Липшица, имеет на нем хотя бы одну точку
минимума.
условию
Липшица, имеет на нем хотя бы одну точку
минимума.
3. Условие (2.5)
означает, что модуль углового коэффициента
любой хорды графика
![]() не превосходит
не превосходит
![]() .
.
Переходя в (2.5) к
пределу при
![]() ,
убеждаемся, что если в некоторой точке
существует касательная к графику функции
,
убеждаемся, что если в некоторой точке
существует касательная к графику функции
![]() ,
то модуль ее углового коэффициента
также не
может
превышать
,
то модуль ее углового коэффициента
также не
может
превышать
![]() .
.
Так, функция
![]() на отрезке
на отрезке
![]() условию Липшица не удовлетворяет, потому
что при
условию Липшица не удовлетворяет, потому
что при
![]() угловой коэффициент касательной
к ее графику
угловой коэффициент касательной
к ее графику
![]() неограниченно
возрастает (рис. 2.5).
неограниченно
возрастает (рис. 2.5).
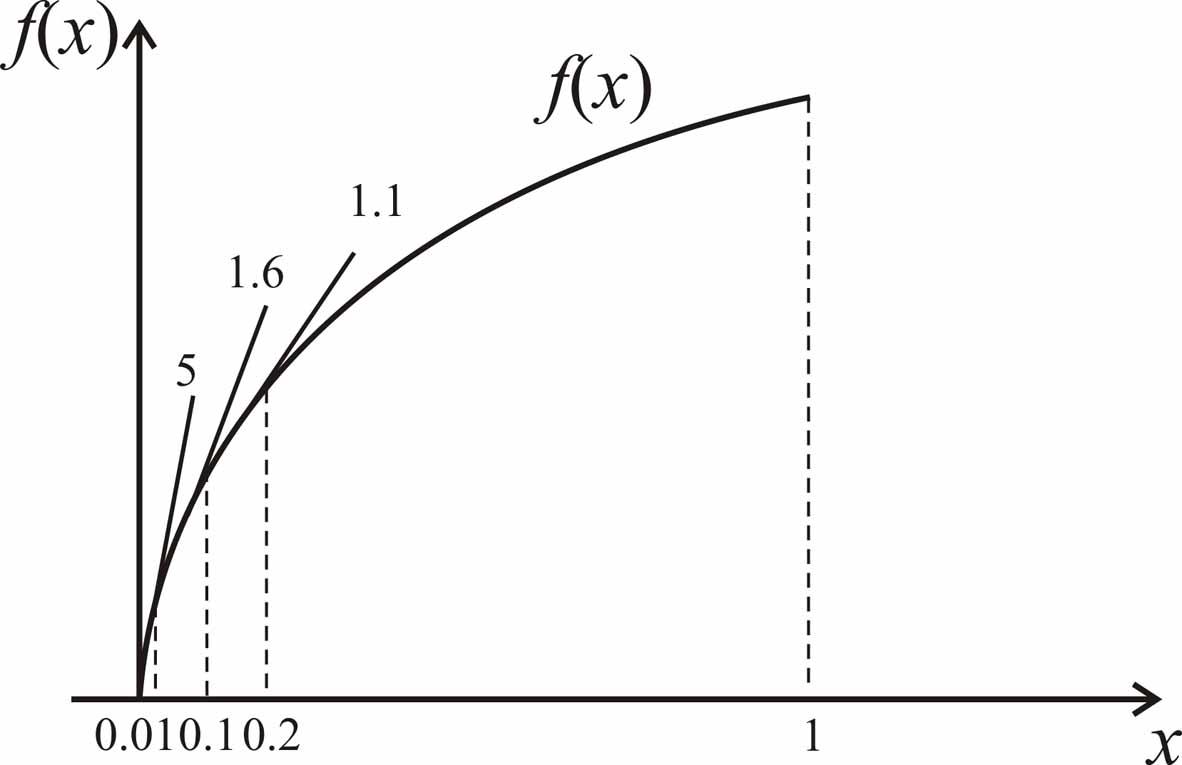
Рис. 2.5. График функции
![]() ,
не удовлетворяющий условию
,
не удовлетворяющий условию
Липшица.
4.
Если функция
![]() имеет на отрезке
имеет на отрезке
![]() непрерывную
производную, то она удовлетворяет на
этом отрезке условию Липшица с константой
непрерывную
производную, то она удовлетворяет на
этом отрезке условию Липшица с константой
![]() .
.
По формуле конечных
приращений для произвольных точек
![]() имеем:
имеем:
![]() ,
где
,
где
![]() - некоторая точка, лежащая между
- некоторая точка, лежащая между
![]() и
и
![]() .
Отсюда с
учетом условия
.
Отсюда с
учетом условия
![]() получаем
неравенство (2.5) для
получаем
неравенство (2.5) для
![]() .
.
5.
Если
![]() ,
а функция
,
а функция
![]() непрерывна на
непрерывна на
![]() и удовлетворяет
условию (2.5) на каждом из отрезков
и удовлетворяет
условию (2.5) на каждом из отрезков
![]() ,
,
![]() ,
с константой
,
с константой
![]() ,
то она удовлетворяет условию Липшица
и на всем отрезке
,
то она удовлетворяет условию Липшица
и на всем отрезке
![]() с константой
с константой
![]() .
.