Лекция №3

Прямые методы одномерного поиска

Для решения задачи минимизации функции на отрезке на практике, как правило, применяют приближенные методы. Они позволяют найти решение этой задачи с необходимой точностью в результате определения конечного числа значений функции и ее производных в некоторых точках отрезка . Методы, использующие только значения функции и не требующие вычисления ее производных, называются прямыми методами минимизации.

Большим достоинством прямых методов является то, что от целе­вой функции не требуется дифференцируемости и, более того, она может быть не задана в аналитическом виде. Единственное, на чем основаны алгоритмы прямых методов минимизации, это возможность определения значений в заданных точках.

Рассмотрим наиболее распространенные на практике прямые методы поиска точки минимума. Самым слабым требованием на функцию , позволяющим использовать эти методы, является ее унимодальность. Поэтому далее будем считать функцию унимодальной на отрезке .

Метод равномерного поиска

Метод равномерного поиска является простейшим из прямых методов минимизации и состоит в следующем.

Разобьем отрезок на равных частей точками деления . Вычислив значения в точках , путем сравнения найдем точку , для которой

(3.1)

Пологая , получим решение задачи (2.1).

Замечание 1. Погрешность определения точки минимума функции методом равномерного поиска не превосходит величины .

В самом деле, пусть из (3.1) является внутренней точкой разбиения отрезка , т.е. (случаи и рассматриваются аналогично). Тогда из соотношения (3.1) с учетом свойства 3 унимодальных функций следует что:

1. , т.е ;

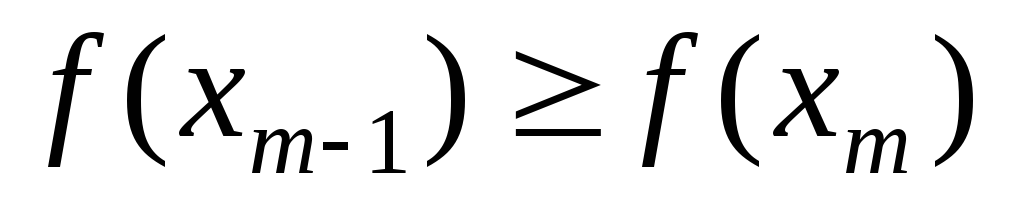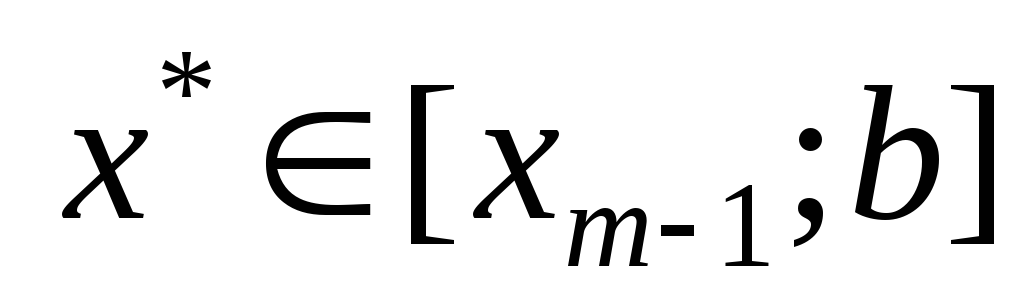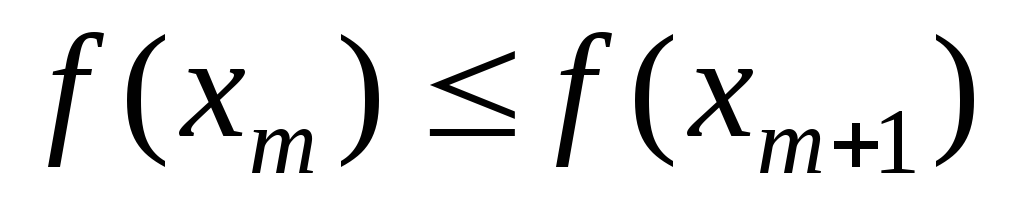2. , т.е..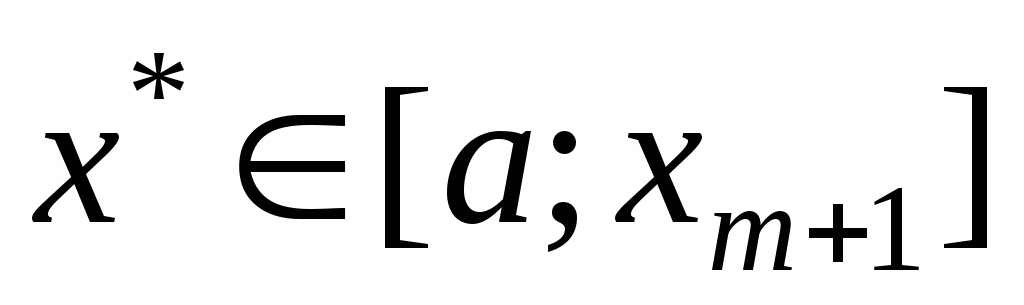

Отсюда получаем, что. Длина последнего отрезка равна , а точка является его серединой. Поэтому - достигнутая точность определения (см. рис. 3.1).

Рис. 3.1.

Таким образом, чтобы обеспечить требуемую точность определения точки , число отрезков разбиения необходимо выбрать из условия , т.е. .

Замечание 2. Пусть реализация метода перебора потребовала вычислений функции . Это означает, что отрезок был разбит на частей и достигнутая точность определения составила . Поэтому точность решения , которую обеспечивает метод перебора в результате вычислений , будет

. (3.2)

Метод поразрядного поиска

Рассмотрим возможности усовершенствования метода перебора с целью уменьшения количества значений , которые необходимо находить в процессе минимизации.

Во-первых, если оказывается, что , то отпадает необходимость вычислять в точках и т.д., как .

Во-вторых, разумно было бы сначала определить отрезок, содержащий , грубо, т.е. найти точку с небольшой точностью, а затем искать ее на этом отрезке с меньшим шагом дискретизации, повышая точность.

Указанные возможности улучшения метода перебора реализованы в методе поразрядного поиска. В этом методе перебор точек отрезка происходит сначала с шагом до тех пор, пока не выполнится условие или пока очередная из этих точек не совпадет с концом отрезка. После этого шаг уменьшается (обычно в 4 раза), и перебор точек с новым шагом производится в противоположном направлении до тех пор, пока значения снова не перестанут уменьшаться или очередная точка не совпадет с другим концом отрезка и т.д. Описанный процесс завершается, когда перебор в данном направлении закончен, а использованный при этом шаг дискретизации не превосходит .

Приведем описание алгоритма метода поразрядного поиска.

Шаг 1: Выбрать начальный шаг . Положить , вычислить .

Шаг2: Положить . Вычислить .

Шаг 3: Сравнить значения и . Если >, то перейти к шагу 4, иначе - к шагу 5.

Шаг 4: Положить =, = Проверить условие . Если , то прейти к шагу 2, иначе - к шагу 5.

Шаг 5: Проверка на окончание поиска: если , то вычисления завершить, полагая = , =, иначе - перейти к шагу 6.

Шаг 6: Изменение направления и шага поиска: положить , =, =. Перейти к шагу 2.