Подставим выражение (11) в формулу (10), получим выражение для амплитуды силы тока при резонансе:

. (13)

Максимум при резонансе тем выше и острее, чем меньше активное сопротивление контура R и чем меньше коэффициент затухания β (рис. 2).

Сдвиг фаз φ между колебаниями тока и внешней э.д.с. в общем случае определяется выражениями:

, (14)

. (15)

При резонансе   .

Отметим некоторые практические применения резонанса.

• Резонансные методы применяют для точного измерения индуктивности и ёмкости систем.

• Резонанс в колебательном контуре используют для выделения из сложного напряжения нужной составляющей при настройке радиоаппаратуры на определённую частоту Ω_i.

Пусть напряжение, приложенное к контуру, равно:

.

Параметры контура L и C подбираются таким образом, чтобы

.

2.Относительная ширина резонансной кривой. Определение добротности контура

Для характеристики колебательной системы пользуются понятием добротности. Добротность характеризует потери энергии в системе и определяется общей формулой:

. (16)

В формуле (16) W(t) – энергия колебательной системы в момент времени t; W(t) – W(t + T) – убыль энергии за 1 период колебаний.

При малых затуханиях добротность колебательного контура определяется приближенной формулой:

. (17)

Пусть вынуждающая э.д.с. представляет собой сумму гармонических э.д.с. с различными циклическими частотами:

. (18)

Результирующий ток в колебательном контуре также будет представлять сумму синусоидальных токов:

. (19)

Вследствие резонанса контур сильнее всего реагирует на ту составляющую э.д.с., частота которой наиболее близка собственной частоте контура ₀ .

Выделение нужной составляющей из сложного напряжения (18) тем эффективней, чем острее резонансная кривая, то есть зависимость .

Остроту резонансного пика можно охарактеризовать с помощью его относительной ширины (или ).

Здесь - разность циклических частот и , соответствующих значению амплитуды тока, равной

. (20)

Получим выражение для относительной ширины резонансной кривой . Зависимость амплитуды тока в колебательном контуре от частоты внешней э.д.с. имеет вид:

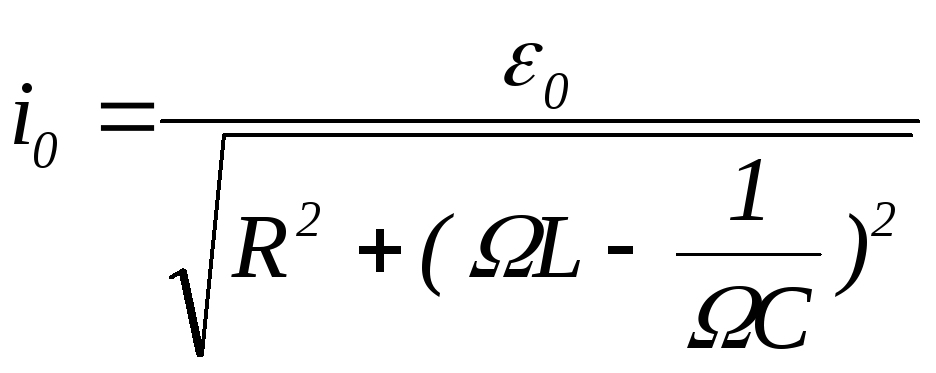. (21)

Амплитуда тока при резонансе равна:

. (22)

Подставляя выражения (20) и (22) в формулу (21), получим:

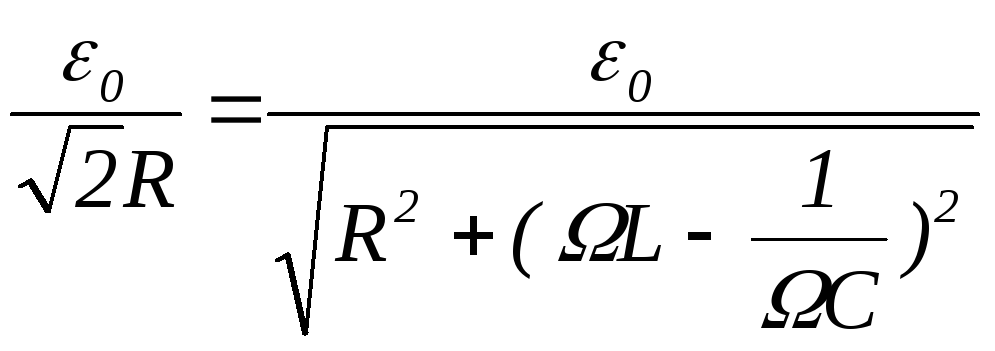(23)

Из выражения (23) следует:

, (24)

или . (25)

Биквадратное уравнение (25) относительно Ω эквивалентно двум квадратным уравнениям:

или , (26)

или . (27)

Так как циклическая частота колебаний Ω не может быть величиной отрицательной, то физический смысл имеют только положительные корни уравнений (26) и (27):

, (28)

. (29)

Разность частот циклических частот и найдём, вычитая из выражения (28) выражение (29), получим:

. (30)

Относительная ширина резонансной кривой равна:

. (31)

Так как циклическая и обычная частоты связаны между собой: и , то . (32)

Сравним выражения (31) и (17), для определения добротности контура получим формулу:

. (33)

Полуширина резонансной кривой и резонансная частота определяются экспериментально (рис. 3).