Числовые множества

Множество натуральных чисел: Множество целых чисел: Множество рациональных чисел: R - множество действительных чисел (рациональных и иррациональных). Иррациональные числа не могут быть представимы в виде дроби, как рациональные. Примеры - число π, √3, и т.д.

Простые и составные числа

Натуральные числа, не имеющие других делителей кроме 1 и самого себя, называются простыми числами. Натуральные числа, имеющие другие делители, называются составными числами. Таким образом, все натуральные числа, за исключением единицы, разбиваются на простые и составные.

Числа  a  и  b - взаимно простые, если наибольший общий делитель этих чисел равен 1.

Процент. Сложный процент

Определение: Процентом называется сотая часть от числа, т.е. 1%А = 0,01А

Сколько процентов составляет число А от числа В?

Решение: x=(A/B)100%

Число А увеличилось на 20%, а затем полученное число уменьшилось на 25%. Как, в итоге, изменилось исходное число?

Решение: 1) А1= (100% + 20%)А = 120%А = 1,2А

2) А2= (100% - 25%)А1 = 75%А1 = 0,75А1 = 0,75 *1,2А = 0,9А = 90%А

3) А2 - А = 90%А - 100%А = -10%. Ответ: число уменьшилось на 10%.

Модуль действительного числа

Формулы сокращенного умножения

Квадратное уравнение ax² + bx + c (a ≠ 0) и теорема Виета

Арифметическая прогрессия

Геометрическая прогрессия

Степени

Корни

Многочлен

Разложение многочленов на множители

 

1.	Если все члены многочлена содержат в качестве сомножителя одно и то же выражение, то его можно вынести за скобки.
2.	Использовать способ группировки.   П р и м е р :    ax+ bx+ ay+ by = ( ax+ bx ) + ( ay + by ) =                           = x( a + b ) +  y ( a +  b ) = ( x + y ) ( a +  b ) .
3.	Использовать формулы сокращённого умножения. Разложение квадратичных многочленов на множители Если  x1 и  x2  - корни квадратного уравнения, то   ax 2 + bx+ c = a ( x –  x1 ) ( x –  x2 )

Функции

Четность и нечетность функций

Функция f называется четной, если для любых x из D(f) f(-x) = f(x) График четной функции симметричен относительно оси OY. Функция f называется нечетной, если для любых x из D(f) f(-x) = - f(x) График нечетной функции симметричен относительно начала координат.

Периодичность функций

Функция называется периодической с периодом Т ≠ 0, если для любого x из D(f) f(x + T) = f(x) = f(x - T). Для построения графика периодичной функции с периодом T достаточно провести построение на отрезке длиной T и полученный график параллельно перенести на расстояние nT вправо и влево вдоль оси OX (n – любое натуральное число).

Возрастание, убывание функций

Функция f возрастает на множестве P, если для любых x1 и x2 из множества P, таких, что x2 > x1, выполнено неравенство f(x2) > f(x1). Функция f убывает на множестве P, если для любых x1 и x2 из множества P, таких, что x2 > x1, выполнено неравенство f(x2) < f(x1).

Формулы тригонометрии

cos2+sin2=1 tgctg=1 Формулы сложения и вычитания аргументов sin(α + β) = sinαcosβ + cosαsinβ sin(α – β) = sinαcosβ – cosαsinβ cos(α – β) = cosαcosβ + sinαsinβ cos(α + β) = cosαcosβ – sinαsinβ  Формулы двойного аргумента sin2α = 2sinαcosα cos2α = cos2α – sin2α Формулы для решения уравнений sinx=a, x=(-1)narcsina+n, nZ (|a|1); cosx=a, x=±arccosa+2n, nZ (|a|1); tgx=a, x=arctga+n, nZ (aR); ctgx=a, x=arcctga+n, nZ (aR); sinx=0, x=n sinx=1, x=/2+2n sinx=-1, x=-/2+2n cosx=0, x=/2+n cosx=1, x=2n cosx=-1, x=+2n, где nZ Тригонометрические неравенства Утверждение 1. Множество решений неравенства sinx > a R, если a < -1; (arcsina + 2k;  - arcsina + 2k), если -1 ≤ a < 1; Пустое множество, если a ≥ 1. Утверждение 2. Множество решений неравенства sinx < a R, если a > 1; (- - arcsina + 2k; arcsina + 2k), если -1 < a ≤ 1; Пустое множество, если a ≤ -1. Утверждение 3. Множество решений неравенства cosx > a R, если a < -1; (2k - arccosa; 2k + arccosa), если -1 ≤ a < 1; Пустое множество, если a ≥ 1. Утверждение 4. Множество решений неравенства cosx < a R, если a > 1; (2k + arccosa; 2(k + 1) - arccosa), если -1 < a ≤ 1; Пустое множество, если a ≤ -1. Утверждение 5. Множество решений неравенства tgx > a Утверждение 6. Множество решений неравенства tgx < a Утверждение 7. Множество решений неравенства ctgx > a (k; arcctga + k). Утверждение 8. Множество решений неравенства ctgx < a (arcctga + k; (k + 1))

Производная и первообразная

Физический смысл производной: Геометрический смысл производной:

Правила вычисления производных

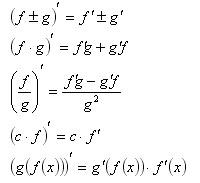
Уравнение касательной

Показательная функция

1

1. Область определения функции − вся числовая прямая.

2. Область значений функции − промежуток (0; +∞).

3. При а>1 функция строго монотонно возрастает на всей числовой прямой. А при а<1 функция строго монотонно убывает на все числовой прямой.

Показательные уравнения

Самое простое показательное уравнение имеет вид ax = b,

(1)

где a > 0, a ≠ 1.

Утверждение 1. Уравнение (1) имеет единственное решение x = log_ab при b > 0 и не имеет решений при b ≤ 0.

Пример 1. Решить уравнения: a) 2^x = -4,    b) 2^x = 4,    c) 2^x = 5.

Решение. a) Множество решений данного уравнения пусто, так как левая часть уравнения положительна при любом x  R (см. свойства показательной функции), а правая часть есть отрицательное число.

b) Используя утверждение 1, получим x = log₂4, то есть x = 2.

c) Аналогично предыдущему примеру получим x = log₂5.

Замечание. Из утверждения 1 следует, что показательное уравнение вида a f(x) = b,

(2)

где a > 0, a ≠ 1 и b > 0 равносильно уравнению f(x) = log_ab.

Пример 2. Решить уравнение   

Решение. Согласно замечанию к утверждению 1

Так как , следовательно , откуда

Утверждение 2. При a > 0, a ≠ 1, уравнения a f(x) = a g(x)

(3)

и f(x) = g(x) равносильны.