Эквивалентность дка и нка

Введем отношение эквивалентности на множестве всех конечных автоматов (распознавателей).

Определение 3.7.

Два автомата эквивалентны, если они допускают один и тот же язык.

Например, автоматы М и М' из предыдущего примера эквива-лентны. Пусть L_D – класс языков, допускаемых детерминиро-ванными конечными автоматами, а L_N – класс языков, допускаемых недетерминированными конечными автоматами. Наша цель - показать, что L_D­­ = L_N. В этом смысле понятия ДКА и НКА равно-сильны. Так как ДКА есть частный случай НКА (когда (q, a) = 1), то, очевидно, L_D­­  L_N. Покажем, что L_{N ­­}  L_D. Для этого для любого НКА М, допускающего язык L(M), достаточно построить ДКА М' такой, что L(M') = L(M), т.е. эквивалентный М.

Рассмотрим преобразование НКА в эквивалентный ДКА сначала на примере.

Пример 3.8.

Обозначим через М следующий НКА М = (Q, , q₀, , F ):

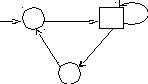q₀ a q₁ a

b 

q₂

Построим эквивалентный ему ДКА M' = (Q', , {q₀}, ', F' ).

1. Положим q₀' ={q₀}.

2. '(q₀', a) = (q₀, a) = {q₁, q₂}, '(q₀', b) = (q₀, b) = .

3. Положим q₁' = {q₁, q₂}, q₂' = .

4. Вычисляем:

'(q₁', a) = (q₁, a)   (q₂, a) = {q₁, q₂}   = {q₁, q₂} = q₁',

'(q₁'_, b) = (q_1, b)  (q₂, b) =   {q₀} = {q₀} = q₀'.

'(q₂', a) =  = q₂', '(q₂', b) =  = q₂'.

Так как новых состояний q' не появилось, то процесс закончен. Получился M':

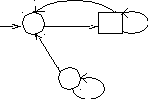b

q'₀ a q'₁ a

b

q'₂ a, b

Легко видеть, что это ДКА и что L(M') = L(M).

Теорема 3.9.

Пусть L – язык, допускаемый недетерминированным конечным автоматом M_N = (Q_N, , _N, q₀, F_N). Тогда существует детерминированный конечный автомат M_D = (Q_D, , _D, q₀, F_D) такой, что L = L(M_D).

Доказательство.

Покажем, как по данному НКА M_N построить ДКА M_D. Будем использовать для этого процедуру (назовем ее Det), описанную ниже, которая по M_N строит диаграмму переходов Г_D автомата M_D. Заметим, что, по определению, каждая вершина Г_D должна иметь  выходящих дуг, помеченных различными символами из . Процедура Det останавливается лишь после того, как будут построены все такие дуги.

Процедура Det:

Шаг 1. Строим граф Г_D, состоящий из единственной вершины {q₀}, которую считаем начальной.

Шаг 2. Повторяем этот шаг до тех пор, пока у каждой построенной вершины в Г_D не будет ровно  выходящих дуг:

1. Берем вершину {q_i, q_j, . . ., q_k}, принадлежащую Г_D, в которой отсутствует выходящая дуга, помеченная некоторым символом а  .

2. Вычисляем _N(q_i, a), _N(q_j, a), . . ., _N(q_k, a).

3. Образуем объединение этих множеств: _N(q_i, a)  _N(q_j, a)  ...  _N(q_k, a) = {q_l, q_m, ..., q_n}.

4. Добавляем в Г_D вершину, помеченную {q_l, q_m, ..., q_n} (если она еще не была помещена в Г_D).

5. Добавляем в Г_D дугу, ведущую из вершины {q_i, q_j, . . ., q_k} в вершину {q_l, q_m, ..., q_n} и помеченную символом а.

Шаг 3. Каждая вершина в Г_D, чья метка содержит некоторую q_f  F, считается финальной и помещается в множество F_D.

Шаг 4. Если M_N допускал строку , то вершина {q₀} также помещается в F_D.

Ясно, что процедура Det сходится (т.е. заканчивает свою работу через конечное число шагов). Действительно, каждый виток цикла в Шаге 2 добавляет дугу в Г_D. Но Г_D может иметь самое большее  дуг, так что этот цикл рано или поздно останавливается.

Покажем теперь, что в результате работы процедуры Det мы получим требуемый автомат M_D (заданный своей диаграммой переходов Г_D). Используем индукцию по длине n входной строки. Очевидно, что при n = 0   L(M_N) тогда и только тогда, когда   L(M_D). Предположим, что для любой строки   *, длина которой   n, существование в Г_N пути, помеченного строкой , из вершины q₀ в вершину q_i влечет существование в Г_D пути, помеченного , из вершины {q₀} в вершину S_i = {..., q_i, ...}, и наоборот.

Пусть теперь  = n + 1. Положим  = а и рассмотрим путь в Г_N из q₀ в q_j, помеченный строкой . Тогда должен существовать путь, помеченный , из q₀ в q_i и дуга (или совокупность дуг) из q_i в q_j, помеченная символом а. По предположению индукции, в Г_D существует путь из {q₀} в S_i, помеченный строкой , а по построению в Г_D должна существовать дуга, помеченная а, из S_i в некоторую вершину, чья метка содержит q_j. Аналогичным образом, несложно провести и обратное рассуждение. Таким образом, видим, что наше утверждение верно и для случая  = n + 1, откуда следует его истинность для любого натурального числа n. Наконец, замечаем, что если _N*(q₀, ) содержит некоторое финальное состояние q_f, то q_f   _D*({q₀}, ) и, значит, _D*({q₀}, )  F_D, и наоборот, если q_f   _D*({q₀}, ), то q_f   _N*(q₀, ). Следовательно, L(M_N) = L(M_D). Теорема доказана.