Лекция 12 Магазинные автоматы Магазинные автоматы

Описание контекстно-свободных языков посредством контекстно-свободных грамматик хорошо согласуется с использованием нотации Бэкуса-Наура при определении языков программирования. Возникает вопрос, существует ли класс автоматов, соответствующий классу КС-языков. Как мы уже видели, конечные автоматы не могут распознавать КС-языки. Интуитивно можно предположить, что это происходит оттого, что конечные автоматы имеют только строго ограниченную – конечную – память, тогда как распознавание контекстно-свободного языка может потребовать запоминания неограниченного объема информации. Например, когда считывается строка из языка L = {aⁿbⁿ | n  0}, мы должны не только проверить, что все символы а предшествуют первому символу b, но также должны запоминать количество символов а. Так как n неограничено, то этот подсчет невозможно сделать, располагая лишь конечной памятью. Для этого требуется машина, которая не содержит такого ограничения. Более того, для некоторых языков, таких, как {^-1}, требуется нечто большее, нежели просто способность к неограниченному счету, а именно способность запоминать и сравнивать последовательность символов в обратном порядке. Это наводит на мысль использовать в качестве устройства памяти магазин (или стек). Так мы приходим к классу машин, называемых магазинными автоматами.

В данной лекции мы исследуем связь между магазинными автоматами и контекстно-свободными языками. Вначале покажем, что в недетерминированном варианте класс таких автоматов допускает в точности семейство КС-языков. Но на этом аналогия с детерминированными и недетерминированными версиями конечных автоматов заканчивается: класс детерминированных магазинных автоматов определяет совершенно другой класс языков, отличных от семейства КС-языков, – так называемых детерминированных КС-языков, образующих собственное подмножество множества всех КС-языков. Этот класс весьма интересен с точки зрения разработки эффективных методов трансляции языков программирования.

Недетерминированные магазинные автоматы

cхематически магазинный автомат можно представить так, как это изображено на рис. 12.1. На каждом шаге устройство управления считывает один символ с входной ленты и одновременно изменяет содержимое магазина посредством обычных стековых операций.

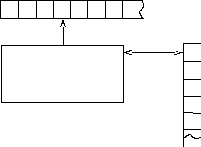Входная лента

Устройство Стек

управления

Рис. 12.1. Магазинный автомат

Каждый следующий шаг, совершаемый устройством управ-ления, определяется данным прочитанным символом с входной ленты, верхним символом стека и внутренним состоянием автомата. Результатом такого шага (или такта работы) является новое состояние устройства управления и замена содержимого вершины стека. Как уже было сказано в лекции 2, мы ограничиваемся рассмотрением лишь автоматов-распознавателей. В этом случае формальное определение выглядит следующим образом.

Определение 12.1.

Недетерминированный магазинный автомат (НМА) определяется как семерка

M = (Q, , V, , q₀, z₀, F),

где

Q = {q₀, q₁, ...,q_n} – конечное множество внутренних состояний автомата;

 – конечное множество символов, называемых входным алфавитом;

V – конечное множество символов, называемое стековым алфавитом;

 – функция переходов автомата, определяемая отображением

: Q  (  {})  V  {S | S – конечное подмножество множества Q  V*};

q₀ – начальное состояние автомата, q₀  Q;

z₀ – начальный символ стека, z₀ V;

F – множество заключительных (или финальных) состояний автомата, F  Q.

Функция  зависит от трех аргументов (q, a, z), из которых q обозначает текущее состояние автомата в данный момент, а – обозреваемый входной символ и z – символ в вершине стека. Значением (q, a, z) является конечное множество пар (q_i, _i), где q_i – следующее состояние автомата, а _i – строка, помещаемая в вершину стека вместо символа а. Заметим, что вторым аргументом у функции  может быть символ пустой строки , означающий, что возможен такт работы автомата, на котором ни один из входных символов не читается. Такой такт называется -переходом. В то же время следует отметить, что третий аргумент не может быть пустым, т.е. переход невозможен, если стек пуст.

Пример 12.2.

Предположим, что множество правил перехода НМА содержит правило

(q₁, a, b) = {( q₂, cd), (q₃, )}.

Если в некоторый момент времени автомат, находясь в состоянии q₁, читает входной символ а и при этом имеет в вершине стека символ b, тогда возможно одно из двух:

- автомат переходит в состояние q₂, а строка cd заменяет символ в вершине стека (при этом в вершине стека оказывается символ с);

- автомат переходит в состояние q₃, при этом символ b удаляется из вершины стека.

Пример 12.3.

Рассмотрим НМА, у которого

Q = {q₀, q₁, q₂, q₃},

 = {a, b},

V = {0, 1},

z₀ = 0,

F = {q₃},

а функция  определяется соотношениями:

(q₀, a, 0) = {(q₁, 10), (q₃, )},

(q₀, , 0) = {(q₃, )},

(q₁, a, 1) = {(q₁, 11)},

(q₁, b, 1) = {(q₂, )},

(q₂, b, 1) = {(q₂, )},

(q₂, , 0) = {(q₃, )}.

Заметим, что функция  не всюду определена. Так, например, для (q₀, b, 0) соотношение, указывающее значение , отсутствует. В этом случае мы интерпретируем значение  как пустое множество, из которого нет ни одной дуги, означающей переход в другое состояние.

Основными соотношениями для  являются следующие два:

первое - (q₁, a, 1) = {(q₁, 11)},

которое добавляет 1 в стек, когда прочитан очередной символ а, и

второе - (q₂, b, 1) = {(q₂, )},

которое удаляет 1 из стека, когда встречается во входной строке b.

Эти два шага подсчитывают число символов а и сравнивают с числом символов b. Автомат находится в состоянии q₁ до тех пор, пока не встретит на ленте первый символ b, и тогда переходит в состояние q₂. Это гарантирует, что ни одно b не встретится раньше последнего а. Анализируя остальные соотношения для , убеждаемся, что автомат переходит в состояние q₃ тогда и только тогда, когда входная строка имеет вид

aⁿbⁿ или а,

т.е. принадлежит языку

L = { aⁿbⁿ | n  0}  {a}.

По аналогии с конечными автоматами мы можем сказать, что НМА допускает язык L.

Пусть q₁ – текущее состояние НМА, a – непрочитанная часть входной строки, b – содержимое стека с символом b в его вершине. Тогда упорядоченная тройка

(q₁, a, b)

называется конфигурацией магазинного автомата. Переход из одной конфигурации в другую с помощью одного такта работы автомата обозначается символом :

(q₁, a, b) (q₂, , )

возможно тогда и только тогда, когда

(q₂, )  (q₁, a, b).

Переходы, включающие произвольное число тактов, будут обозначаться (или для случая, когда хотя бы один шаг действительно имеет место). Чтобы идентифицировать переход, совершенный данным автоматом М, будем использовать символ _M.

Определение 12.4.

Пусть М = (Q, , V, , q₀, z₀, F) – недетерминированный магазинный автомат. Тогда язык, допускаемый автоматом М, – это множество

L(M) = { |    * и (q₀, , z₀) _M (q_f, , ), q_f  F,   V*}.

Таким образом, язык, допускаемый НМА М, это множество строк в алфавите , которые переводят автомат М из начального состояния в финальное состояние после прочтения входной строки (при этом содержимое стека не играет никакой роли и может быть любым).

Пример 12.5.

Построить НМА для языка

L = { |   {a, b}* и n_a() = n_b()},

где n_a() и n_b() обозначают число символов а и b в строке .

Нетрудно проверить, что НМА

M = ({q₀, q_f), {a, b}, {0, 1, z}, , q₀, z, {q_f}),

где  определяется соотношениями:

(q_o, , z) = {(q_f, z)},

(q_o, a, z) = {(q₀, 0z)},

(q_o, b, z) = {(q₀, 1z)},

(q_o, a, 0) = {(q₀, 00)},

(q_o, b, 0) = {(q₀, )},

(q_o, a, 1) = {(q₀, )},

(q_o, b, 1) = {(q₀, 11)},

действительно допускает язык L. В частности, при чтении строки baab НМА М совершает следующие такты:

(q_o, baab, z) (q_o, aab, 1z) (q_o, ab, z)

(q_o, b, 0z) (q_o, , z) (q_f, , z),

следовательно, эта строка допускается автоматом М.

Пример 12.6.

Построить НМА, допускающий язык

L = {^-1 |   {a, b}⁺}.

Для построения недетерминированного магазинного автомата, распознающего данный язык, воспользуемся тем фактом, что символы извлекаются из стека в порядке, обратном тому, в котором они туда заносились. Во время чтения первой половины входной строки мы помещаем последовательно читаемые символы в стек, а при чтении второй половины строки мы сравниваем текущий входной символ с тем, который находится в вершине стека, продолжая это сравнение до окончания входной строки. Так как символы извлекаются из стека в порядке, обратном тому, в котором они заносились в стек, то полностью сравнение будет успешным тогда и только тогда, когда входная строка имеет вид ^-1 для некоторой строки   {a, b}⁺.

Очевидной трудностью здесь является то, что мы не знаем, где середина входной строки, т.е. где кончается  и начинается ^-1. Но недетерминированный характер автомата приходит нам на помощь: НМА правильно указывает, где середина, и сигнализирует своими состояниями об этом. Итак, строим НМА М = (Q, , V, , q₀, z₀, F), где Q = {q₀, q₁, q₂},

 = {a, b},

V = {a, b, z},

F = {q₂}.

Соотношения, определяющие функцию , можно разбить на несколько групп:

а) команды, записывающие  в стек:

(q_o, а, a) = {(q₀, aa)},

(q_o, b, a) = {(q₀, ba)},

(q_o, a, b) = {(q₀, ab)},

(q_o, b, b) = {(q₀, bb)},

(q_o, a, z) = {(q₀, az)},

(q_o, b, z) = {(q₀, bz)},

b) команды, определяющие середину строки, что сигнализируется переходом из состояния q₀ в q₁:

(q_o, , a) = {(q₁, a)},

(q_o, , b) = {(q₁, b)},

c) команды, сравнивающие ^-1 с содержимым стека:

(q₁, а, a) = {( q₁, )},

(q₁, b, b) = {(q₁, )},

(q₁, , z) = {(q₂, z}.

Рассмотрим последовательность тактов при распознавании этим автоматом строки abba:

(q_o, abba, z) (q_o, bba, az) (q_o, ba, baz)

(q₁, ba, baz) (q₁, a, az) (q₁, , z) (q₂, , z).

Недетерминированный выбор при определении середины входной строки возникает на третьем такте. На этом шаге НМА имеет конфигурацию (q₀, ba, baz) и две возможности для следующего шага: один из них использует команду

(q_o, b, b) = {(q₀, bb)}

и порождает такт

(q₀, ba, baz) (q₀, a, bbaz),

а другой – порождается использованной выше командой

(q_o, , b) = {(q₁, b)},

и только он ведет к распознаванию входной строки.