1.4.2 Полученные решения
Максимум заданной функции находится в нуле.
1.5 Многомерная оптимизация
-
Общие сведения
Один
из подходов к задаче поиска экстремума
функции
векторного аргумента размерности
(как
и в случае одномерного поиска) заключается
в решении системы нелинейных алгебраических
уравнений
,
,
Пусть
необходимо найти минимум функции
многих переменных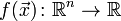 
.
Эта задача равносильна задаче нахождения
нуля градиента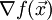 
.
Применим изложенный выше метод Ньютона:
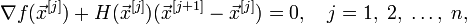
где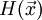 
— гессиан
функции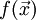 
.
В более удобном итеративном виде это выражение выглядит так:
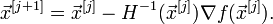
Следует отметить, что в случае квадратичной функции метод Ньютона находит экстремум за одну итерацию.
1.5.2 Полученные решения
Минимум функции находится в точке: (-5; 1).
2 Исходные тексты
Решение СЛАУ:
clear all;
a = 1.5;
b = 0.4;
S = [ 2.1+a -4.5 -2 19.07-b;
3 2.5 4.3-a 3.21+b;
-6 3.5+a 2.5 -18.25];
Xs = solve('3.6*x-4.5*y-2*z=18.67','3*x+2.5*y+2.8*z=3.61','-6*x+5*y+2.5*z=-18.25');
D = S(1:3,1:3);
% Gauss
G = S;
tic;
% represent in triangle form
for k = 1:2
for i = (k+1):3
m(i) = G(i,k) / G(k,k);
for j = 1:4
G(i,j) = G(i,j) - m(i)*G(k,j);
end;
end;
end;
% reverse lapse
gx(3) = G(3,4)/G(3,3);
gx(2) = (G(2,4)-G(2,3)*gx(3))/G(2,2);
gx(1) = (G(1,4)-G(1,2)*gx(2) - G(1,3)*gx(3))/G(1,1);
tms(2) = toc;
sprintf('Решение методом Гаусса:')
gx
%LU decomposition
tic;
B = [D(1,1) 0 0; D(2,1) 0 0; D(3,1) 0 0];
C = [1 0 0; 0 1 0; 0 0 1];
% G(row , column)
% first stage
for i = 1:3
C(1,i) = D(1,i)/B(1,1);
end;
for j = 2:3
for i = j:3
s = 0;
for k = 1:j-1
s = s + B(i,k)*C(k,j);
end;
B(i,j) = D(i,j) - s;
end;
for i = j+1:3
s = 0;
for k = 1:j-1
s = s + B(j,k) * C(k,i);
end;
C(j,i) = (1/B(j,j)) * (D(j,i) - s);
end;
end;
y(1) = S(1,4)/B(1,1);
y(2) = (S(2,4) - B(2,1)*y(1))/B(2,2);
y(3) = (S(3,4) - B(3,1)*y(1) - B(3,2)*y(2))/B(3,3);
xh(3) = y(3);
xh(2) = y(2) - C(2,3)*xh(3);
xh(1) = y(1) - C(1,3)*xh(3) - C(1,2)*xh(2);
tms(3) = toc;
sprintf('Решение методом LU-разложения:')
xh
% Gauss-Jordan
tic
GJ = S;
for l = 1:3
for i = 1:3
if l == i
continue;
end;
m(i) = GJ(i,l)/GJ(l,l);
for j = 1:4
GJ(i,j) = GJ(i,j) - m(i)*GJ(l,j);
end;
end;
end;
xgj(1) = GJ(1,4)/GJ(1,1);
xgj(2) = GJ(2,4)/GJ(2,2);
xgj(3) = GJ(3,4)/GJ(3,3);
tms(4) = toc;
sprintf('Решение методом Гаусcа-Жордана:')
xgj
clear all; %очищаем память
e = 0.0001; %погрешность
%----------------- начальные условия/постановка задачи ------------
S = [ 7 0.09 -0.03 5.8;
0.09 4 -0.15 7.8
0.04 -0.08 6 16.2];
%------------------------------------------------------------------
Xs = solve('7*x+0.09*y-0.03*z=5.8','0.09*x+4*y-0.15*z=7.8','0.04*x-0.08*y+6*z=16.2');
sprintf('Рассматриваемая система:')
S %выводим матрицу коэфициентов системы
%проверка на сходимость итерационных методов
%модули диагональных коэффициентов для каждого уравнения системы должны быть больше
%модулей всех остальных коэффициентов (без учета свободных членов).
shod = 1;
for i = 1:3
s = 0;
for j = 1:3
if (i ~= j)
s = s + abs(S(i,j));
end;
end;
if (abs(S(i,i))<=s)
shod = 0;
end;
end;
if (shod == 0)
sprintf('Не выполняется условие сходимости метода простой итерации.')
else
% ------------------------------ Метод простой итерации -----------
mS = S;
%преобразуем систему , решим первое уравнение отностильно x(1), второе
%отностильно x(2) и т.д.
mS(1,1) = 0;
for i =1:3
for j=1:3
mS(i,4) = S(i,4)/S(i,i); % вычисляем свободный коэффициент
%вычисляем коэффициенты при X
if (i == j) %при i=j
mS(i,j) = 0;
else % иначе
mS(i,j) = - (S(i,j)/S(i,i));
end;
end;
end;
% решаем систему
maxOst = 1;
k=0;
lx = [1:3]; % X на k-1 итерации
while maxOst>e %проверка на достижение точки остановы
if (k == 0)
%выбираем первичное приближение решения системы
for i = 1:3
x(i) = mS(i,4);
end;
else
% вычисляем следующие приблежение X
for i = 1:3
x(i) = mS(i,4);
s = 0;
for j=1:3
s = s + mS(i,j)*lx(j);
end;
x(i) = x(i) + s;
end;
end;
%вычиление условия точки остановы
maxOst = abs(lx(1)-x(1));
for i=2:3
if (maxOst<abs(lx(i)-x(i)) )
maxOst = abs(lx(i)-x(i));
end;
end;
k=k+1;
lx = x;
end;
sprintf('Ответ полученный методом простой итериции (Всего %i итераций, %.10f сек. ):',k,tms(1))
x %выводим ответ
%----------------------- Метод Зейделя -----------------------------------
%выбираем первичное приближение решения системы
for i = 1:3
zx(i) = S(i,4);
end;
maxOst = 1;
lx = zx;
k=0;
while maxOst>e %проверяем достижение точки остановы
% вычисляем следующие приблежение X
zx(1) = (1/S(1,1))*(S(1,4)-S(1,2)*lx(1)-S(1,3)*lx(3));
zx(2) = (1/S(2,2))*(S(2,4)-S(2,1)*zx(1)-S(2,3)*lx(3));
zx(3) = (1/S(3,3))*(S(3,4)-S(3,1)*zx(1)-S(3,2)*zx(2));
%вычиление условия точки остановы
if k > 0
maxOst = abs(lx(1)-zx(1));
for i=2:3
if (maxOst<abs(lx(i)-zx(i)))
maxOst = abs(lx(i)-zx(i));
end;
end;
end;
lx = zx;
k = k +1;
end;
sprintf('Ответ полученный методом Зейделя (Всего %i итераций, %.10f сек. ):',k,tms(2))
zx %выводим ответ
%Интерполирование функций
clear all; %очищаем память
% ----------------- постановка задачи --------------------------
x = [0 0.4 0.8 1.2 1.6 2.0];
y = [1 0.9211 0.6967 0.3624 (-0.0292) (-0.4161)];
e = 0.000001;
eE = 1.05;
% функция cos(x);
% --------------------------------------------------------------
% ------------------------ формула Лагранжа --------------------
s = 0;
for i = 1:6
s2 = 1;
for j = 1:6
if i ~= j
s2 = s2*( (eE - x(j))/(x(i)-x(j)) );
end;
end;
s = s + y(i)*s2;
end;
R = abs(cos(eE)-s);
sprintf('Точное значение функции в точке %.7f , по формуле Лагранжа %.7f , погрешность %.7f ',cos(eE),s,R)
% -------------------- Кусочно-линейная интерполирование --------
i=4;
yk = ( (eE-x(i-1))*(y(i)-y(i-1)) + y(i-1)*(x(i)-x(i-1)) ) / (x(i) - x(i-1));
Ry = abs(cos(eE)-yk); %погрешность
sprintf('Точное значение функции в точке %.7f , применяя кусочно-линейное интерполирование %.7f , погрешность %.7f ',cos(eE),yk,Ry)
% ---------- Кусочно-квадротичное интерполирование --------------
ys = 0;
for i = 1:6
%крайние точки
if (i == 1)
ys = ys + y(1)* ( ( (eE - x(2))*(eE - x(3)) ) / ( (x(1)-x(2))*(x(1)-x(3)) ) );
continue;
end;
if (i==6)
ys = ys + y(6)* ( ( (eE - x(4))*(eE - x(5)) ) / ( (x(1)-x(2))*(x(4)-x(5)) ) );
continue;
end;
ys = ys + y(i)* ( ( (eE - x(i-1))*(eE - x(i+1)) ) / ( (x(i) - x(i-1)) * (x(i) - x(i+1)) ) );
end;
Rys = abs(cos(eE)-ys); %погрешность
sprintf('Точное значение функции в точке %.7f , применяя кусочно-квадратичное интерполирование %.7f , погрешность %.7f ',cos(eE),ys,Rys)
%-------------------------- Сплайны ------------------------------
N=4;
h = x(N) - x(N-1);
%вычисление коэффициентов
a = y(N);
c = [4 1 1 0;
1 4 1 0;
1 1 4 0];
dy(1) = y(1);
for i = 2:4
dy(i) = y(i)-y(i-1);
dy(i+1) = y(i+1)-y(i);
d2y = dy(i) - dy(i-1);
c(i-1,4) = (3*d2y)/(h*h);
end;
c = jrd(c);
d = (c(N+1) - c(N))/(3*h) ;
b = dy(N+1)/h - (c(N+1)+2*c(N))*(h/3);
c = c(N);
% вычисление згначения функции
F = a + b*(eE-x(N))+c*realpow((eE-x(N)),2)+d*realpow((eE-x(N)),3);
Rys = abs(cos(eE)-F); %погрешность
sprintf('Точное значение функции в точке %.7f , применяя интерполирование сплайнами %.7f , погрешность %.7f ',cos(eE),F,Rys)
%Решение ДУ
clear all;
x0 = 1;
y0 =0;
b = 2.5;
h = 0.1;
%Метод Рунге-Кутты
function f = runge-kutta-matlab( x,y )
f=(1+exp(x/y))/(exp(x/y)*(x/y-1));
end
function [ x y ] = runge-kutta( x0,y0,b,h )
x=[];
y=[];
while (x0<=b+h)
x=[x x0];
y=[y y0];
k1=h*runge-kutta-matlab(x0,y0);
k2=h*runge-kutta-matlab(x0+h/2,y0+k1/2);
k3=h*runge-kutta-matlab(x0+h/2,y0+k2/2);
k4=h*runge-kutta-matlab(x0+h,y0+k3);
y0=y0+1/6*(k1+2*k2+2*k3+k4);
x0=x0+h;
end
end
%Модифицированный метод Эйлера
clear all;
x0 = 1;
y0 = 2;
b = 2;
h = 0.1;
function f = euler-matlab( x,y )
f=(2*x*y^3)/(1-(x^2)*(y^2));
end
function [x y] = euler( x0,y0,b,h )
x=[];
y=[];
while (x0<=b)
x=[x x0];
y=[y y0];
xt=x0+h/2;
yt=y0+(h/2)*(euler-matlab(x0,y0));
y0=y0+h*euler-matlab(xt,yt);
x0=x0+h;
end
end
%Одномерная оптимизация
function y = f(x)
y = 4 - 3 * x ^ 2;
end
function y = fstroke(x)
y = -6*x;
end
function y = fstrokestroke(x)
y = -6;
end
x = [];
x(1) = -10;
h = 0.01;
k = 2;
x(2) = 0;
if (f(x(1) - h) <= f(x(1)) && f(x(1)) <= f(x(1) + h))
x(2) = x(1) + h;
goto(step4);
elseif (f(x(1) - h) >= f(x(1)) && f(x(1)) >= f(x(1) + h))
x(2) = x(1) - h;
h = -h;
goto(step4);
else
a = x(1) - h;
b = x(1) + h;
goto (ret);
end
%LABEL step4
x(k + 1) = x(k) + (2 ^ k) * h;
if (f(x(k) + 1) >= f(x(k)))
k = k + 1;
goto (step4);
end
if (h > 0)
a = x(k - 1);
b = x(k + 1);
goto(ret);
else
b = x(k - 1);
a = x(k + 1);
goto(ret);
end
%LABEL ret
answ = 0;
answ0 = 0;
if (f(a) >= f(b))
answ0 = a - f(a)/(f(b) - f(a)) * (b - a);
else
answ0 = b - f(b)/(f(b) - f(a)) * (b - a);
end
answ = answ0 - fstroke(answ0)/fstrokestroke(answ0);
%ruthless and pointless. I diff by hand!
while abs(answ0 - answ) >= h
answ0 = answ;
answ = answ0 - fstroke(answ0)/fstrokestroke(answ0);
end
sprintf('Максимум в точке:');
answ
clear all;
%Многомерная оптимизация
function z = dfdx(x, y)
z = 2 * x + 10 * y;
end
function z = dfdy(x, y)
z = 10 * x + 52 * y + 2;
end
%начальное приближение
x = [8 10];
%гессиан
H = [2 10; 10 52];
%градиент
Del = [dfdx(x(1), x(2)), dfdy(x(1), x(2))];
tmp = x;
x = x - transpose(inv(H) * transpose(Del));
while ((abs(tmp(1) - x(1)) >= 0.35) && (abs(tmp(2) - x(2)) >= 0.35))
tmp = x;
Del = [dfdx(x(1), x(2)), dfdy(x(1), x(2))];
x = x - (transpose(inv(H) * transpose(Del)));
end
sprintf('x =');
x(1)
sprintf('y =');
x(2)
ЗАКЛЮЧЕНИЕ
Быстро развивающимся направлением вычислительной математики являются численные методы. Задача оптимизации состоит в изучении экстремальных (наибольших или наименьших) значений функционалов на множествах, как правило, весьма сложной структуры. В первую очередь следует упомянуть задачиматематического программирования (в том числе линейного и динамического), к к-рым сводятся многие задачи экономики. К задачам оптимизации примыкают минимаксные задачи (и соответствующие численные методы), возникающие при решении задач исследования операций и теории игр. Особенно сложные задачи типа minmaxminmax возникают при решении многошаговых (динамически развивающихся) игр. Здесь даже математич. эксперимент (проигрывание вариантов поведения играющих) невозможен без использования мощных ЭВМ.
Применение ЭВМ к решению сложных задач, в особенности задач больших размеров, вызвало к жизни одно из главных направлений в теории численных методов - исследования устойчивости методов и алгоритмов к различного рода ошибкам (в том числе к ошибкам округления).
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Доценко С. В. Численные методы информатики. Конспект лекций – СевГТУ 2000 г.
-
Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн Алгоритмы: построение и анализ = Introduction to Algorithms. — 2-е изд. — М.: «Вильямс», 2006. — С. 1296
-
Е. Алексеев «Решение задач вычислительной математики в пакетах Mathcad 12, MATLAB 7, Maple 9», 2006 г., 496 стр.