6.3. Метод прогонки

Метод прогонки является частным случаем метода Гаусса, применяемого к системам с трехдиагональной матрицей. Такие системы обычно записывают в каноническом виде

, 1  i  n, a₁ = c_n = 0. (6.11)

Формула (6.11) называется разностным уравнением второго порядка или трехточечным уравнением. Равенство a₁ = c_n =0 означает наличие свободных концов функции, то есть на концах отрезка вторая производная аппроксимируемой разностным уравнением функции равна нулю.

Будем искать в виде итерационной процедуры:

, i = n, n-1, …, 1. (6.12)

Подставим (6.12) в (6.11):

, . (6.13)

Выражая отсюда x_i через x_i+1 получим

. (6.14)

Сравнив (6.14) с (6.12), видим, что

С учётом вышесказанного процедура решения системы (6.11) реализуется за два шага.

Первый шаг (прямой ход)  определение промежуточных переменных:

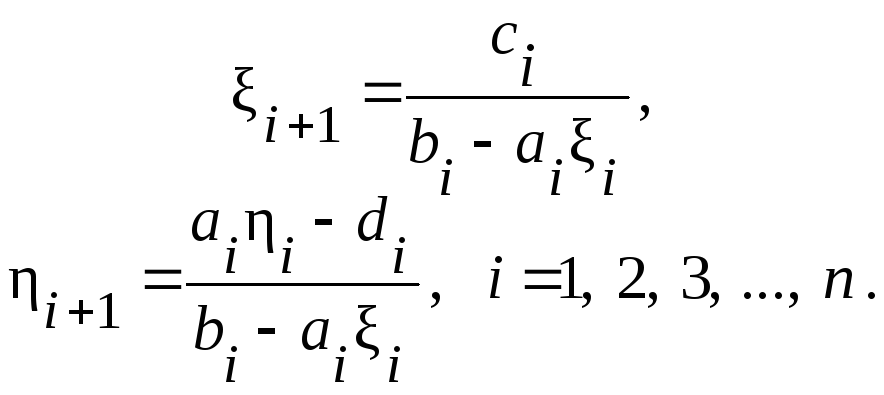
Значения можно принять любыми, так как они умножаются на а₁ =0. Поэтому принимаем . Зная начальные значения , можно найти все значения , i = 1, 2, 3, ..., n.

Зная , на втором шаге (обратном ходе) находим значения неизвестных , i = n, n-1, …, 1, приняв во внимание, что можно принять равным 0, так как c_n = 0.

Примечание. Явная схема решения уравнения (6.6) учитывает значение краевых условий только на предыдущем временном шаге. Этот метод прост в реализации, но обладает меньшей точностью решения задачи, чем при неявной схеме. Условие устойчивости решения при явной схеме [2] можно записать в виде . Решение уравнения по неявной схеме всегда устойчиво, но согласно [2] устойчивость решения не гарантирует его точности. Известно несколько методов составления разностных схем:

- метод разностной аппроксимации (рассмотрен выше);

- интегро-интерполяционный метод;

- метод неопределённых коэффициентов.

Наиболее точным из них является интегро-интерполяционный метод, но это и самый сложный в реализации метод.

6.4. Комбинированный метод решения смешанной краевой задачи

Этот метод основан на использовании интерполирования методом сплайнов переменной на множестве g (6.3). Как известно, интерполирование сплайнами основано на аппроксимации функции на каждом интервале , полиномом третьей степени [2].

 (6.15)

Проинтегрировав это уравнение дважды, получим

. (6.16)

Так как (x) аппроксимирует функцию u, то (x) аппроксимирует . Используя значения второй производной (x) в каждой точке множества g, можно численно проинтегрировать уравнение (6.6) по времени и получить значение переменной u на следующем временном слое. Данный метод ближе всего к неявной схеме. Действительно, коэффициенты находятся методом прогонки, но эти коэффициенты находятся на текущем m-м временном слое, а оценка значения второй производной используется для расчета значения переменной на следующем m+1 слое. В отличие от этого, неявная схема обеспечивает расчет сразу на m+1 слое. Практическое использование этих двух способов на одной и той же задаче,  прогрев тела через некоторую границу,  показал, что предлагаемый способ обладает большей точностью, чем метод решения задачи по неявной схеме. Вторым очень важным достоинством предлагаемого метода является то, что в методе сплайнов концы кривой интерполирования свободны, то есть они представляют собой отрезки прямой, углы наклона которых можно задавать произвольно. А это позволяет в задаче теплопроводности определять величину теплового потока (), передаваемого телу через границу. Это важно учитывать, так как на практике мощность нагревателя, от которого тело нагревается, ограничена. Третьим достоинством данного метода является его простота. Интерполяция сплайнами обычно реализуется как библиотечная функция и использование её не вызывает особых проблем.