123

«Численные Методы в Механике»

Лабораторная работа № 11

Тема: «Приближенное вычисление производной от таблично заданной функции на основе интерполяционных многочленов Лагранжа и Ньютона»

Постановка задачи

Пусть исследуемая функция либо задана таблично на интервале с постоянным шагом , либо имеет достаточно сложный функциональный вид, затрудняющий определение производной .

Необходимо построить алгоритм вычисления значения производной в заданной точке , воспользовавшись интерполяционным многочленом:

а) – Лагранжа:

, где ; (11.1)

б) – Ньютона (первая и вторая формулы соответственно):

, (11.2)

. (11.3)

Предполагается, что исходная таблица функции содержит достаточно большое количество отрезков интерполирования, например . Очевидно, что для решения нашей задачи строить интерполяционные многочлены степени нерационально и, кроме того, погрешность самих арифметических операций может существенно возрастать при больших степенях многочленов.

В качестве условия задачи примем следующие границы для степени интерполяционных многочленов (11.1)–(11.3), аппроксимирующих нашу табличную функцию .

Напомним, что для построения интерполяционного многочлена степени нам необходимо использовать отрезков интерполирования (или, что то же, узел интерполирования).

Программа, разработанная Вами, должна вычислять таблицу значений производной в узлах исходной таблицы данных, а также в средних ее точках, т.е. для , где и .

Таблиц производных должно быть две – для метода интерполирования по Лагранжу и для метода интерполирования по Ньютону соответственно. В каждой таблице должны приводиться точные значения производной, а также абсолютная и относительная погрешности их вычисления.

Исходные данные (аппроксимируемые функции) необходимо брать из таблицы «Вариантов заданий» к Лабораторной работе № 8. Значения параметров и задаются пользователем при непосредственном выполнении программы.

Предварительные рекомендации

Для успешного выполнения данной лабораторной работы Вам следует ознакомиться со следующими рекомендациями.

Рассмотрим особенности реализации алгоритма интерполирования по Лагранжу.

Пусть установлено, что исследуемое значение аргумента принадлежит -му отрезку интерполирования, т.е. .

В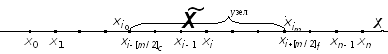ведем обозначение для частичного интервала интерполирования, содержащего в себе отрезок , а также ровно отрезков интерполирования ( узел) из исходной таблицы данных:

Наша первоочередная задача – вычислить индексы и узлов-границ частичного интервала при условии, что отрезок должен располагаться «посередине» этого интервала.

Такой подход обеспечит наилучшее для многочлена Лагранжа «качество» аппроксимации табличной функции и ее производной для значения аргумента .

Таким образом, алгоритм вычисления значений индексов и представляет собой самостоятельную проблему. По этой причине мы будем его разрабатывать и отлаживать в рамках отдельного, вспомогательного консольного приложения (например, на Fortran).

Указанный алгоритм должен учитывать следующие моменты:

• порядок интерполяционного многочлена может быть как четным, так и нечетным числом;

• значение 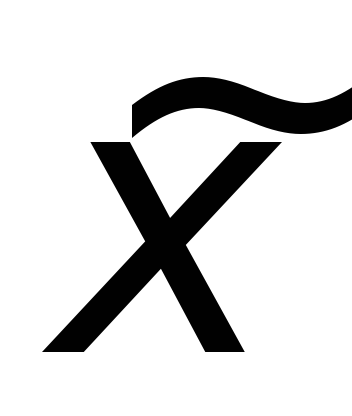аргумента может быть близко к границам ( 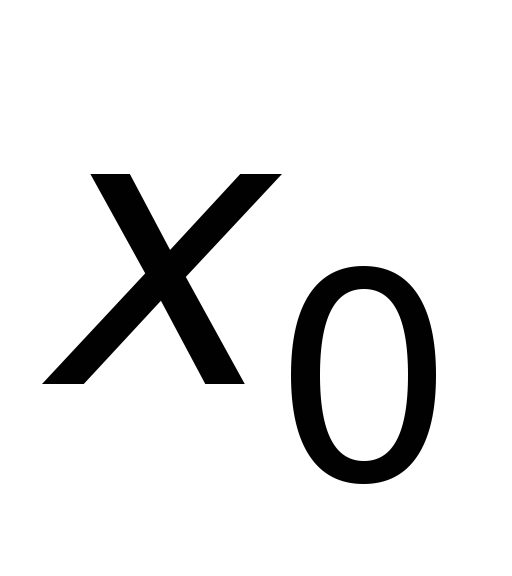или 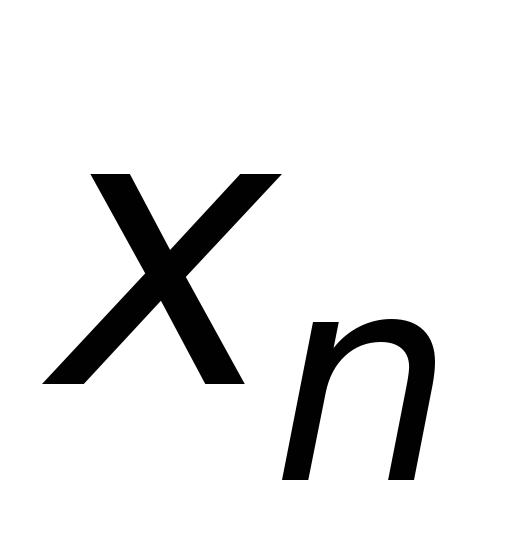) исходной таблицы данных, так что указанный выше принцип размещения отрезка 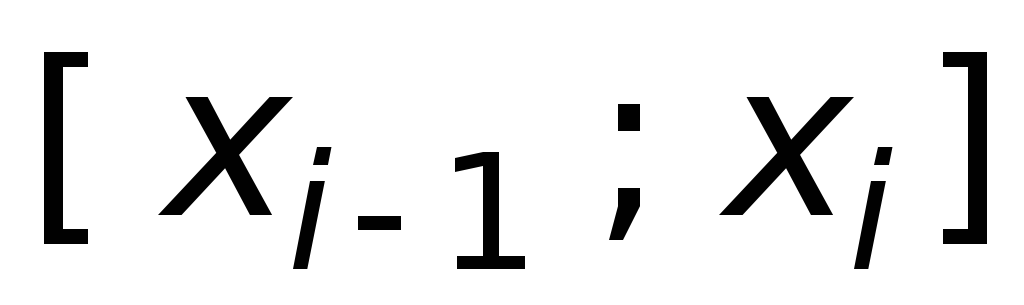«посередине» интервала 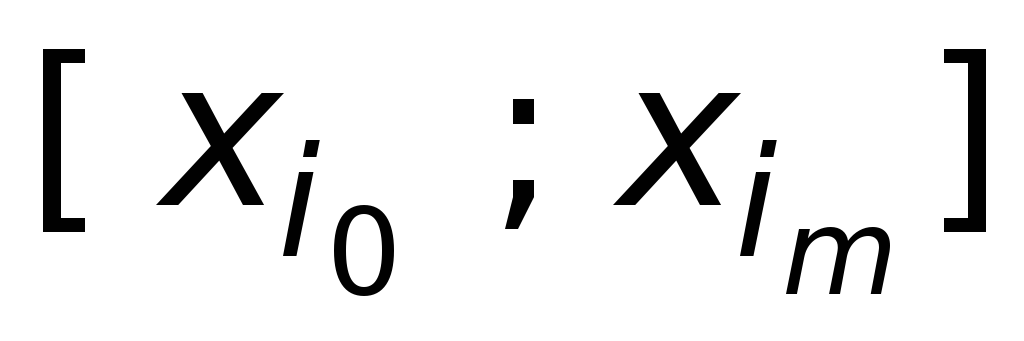не может быть реализован.

Будем определять индексы и с использованием известных арифметических функций и , выполняющих преобразование действительного числа к целому:

(11.4)

где для четных значений будет (11.5)

а для нечетных значений будет (11.6)

Например, при имеем см. рисунок выше по тексту, (11.7)

а при имеем (11.8)

Такие результаты обусловлены правилами функций и . Их суть легко усвоить из примера:

(11.9)

Следовательно, первая функция – – у положительного действительного числа просто «отбрасывает» дробную часть, а вторая функция – – увеличивает до ближайшего целого.

Если при реализации алгоритма (11.4) индекс оказывается отрицательным, то это означает, что значение аргумента размещается «близко» к узлу и интервал нельзя расположить «посередине» интервала .

В таком случае мы в качестве индекса будем брать , т.е. , а индексу дадим значение , т.е. . (11.10)

Если же при реализации алгоритма (11.4) индекс окажется больше, чем , то это означает, что значение аргумента размещается «близко» к узлу и интервал также нельзя расположить «посередине» интервала .

В этой ситуации мы поступим аналогично предыдущему случаю: индексу дадим значение , т.е. , а индексу – значение , т.е. . (11.11)

Во всех трех перечисленных случаях для частичного интервала интерполирования будет выделено из основной таблицы ровно интервалов ( узел интерполирования).

Все выше сказанное реализуем в отдельном проекте AddAlgorithm_11 консольного приложения на языке программирования Fortran.

Для простоты анализа результатов массив узлов исходной таблицы разместим в точках с целыми значениями координат, например, равными их индексу, а в качестве «исследуемых» точек будем выбирать середины полученных отрезков интерполирования.

При таких условиях код основной программной единицы будет следующим:

Ниже приводятся результаты для одного из тестовых расчетов:

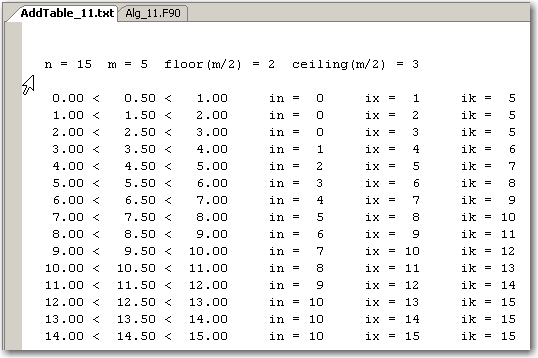
Вернемся теперь к формуле (11.1). С использованием новой безразмерной переменной ее можно представить в виде:

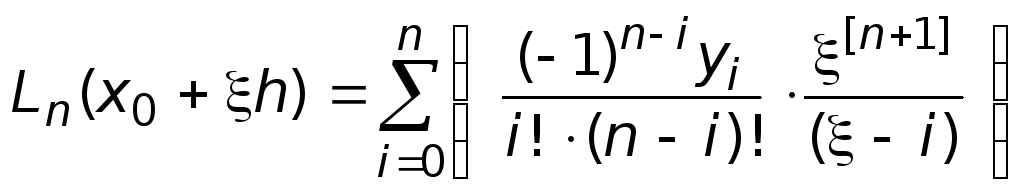, где . (11.12)

Каждое е слагаемое, стоящее под знаком суммы в (11.12) представляет собой произведение коэффициента на многочлен степени , записанный в виде произведения , в котором отсутствует скобка .

Производная от многочлена Лагранжа будет иметь вид:

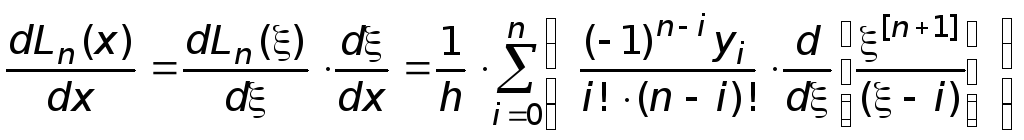. (11.13)

Таким образом, каждое е слагаемое, стоящее под знаком суммы в (11.13) будет представлять собой произведение коэффициента на производную от произведения .

Отметим, что в этом произведении всего сомножителей, поскольку отсутствует скобка .

Производная произведения, в свою очередь, может быть представлена в виде следующей суммы:

. (11.14)

Каждое е слагаемое такой суммы является произведением из сомножителей, в котором отсутствуют скобки и .

Подведем общий итог рассуждениям. Формула (11.13) представляет собой сумму из слагаемого (по от 0 до ), каждое из которых представляет собой сумму (11.14) из слагаемых (по от 0 до , без слагаемого с ), каждое из которых, в свою очередь, есть произведение из сомножителей (по от 0 до , без сомножителей и ).

Если при построении многочлена (11.13) мы будем использовать только отрезков интерполирования, непосредственно примыкающих к значению , то нам придется воспользоваться уже отлаженным алгоритмом определения границ частичного интервала интерполирования.

В этом случае параметр в формулах (11.13) и (11.14) будет принимать значение , а безразмерная переменная будет вычисляться как , а сама формула (11.13) примет вид

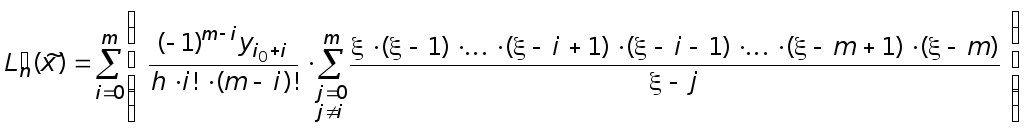. (11.15)

Остается только реализовать формулу (11.15) в виде соответствующей программной единицы.

Обратимся теперь к формулам (11.2) и (11.3) интерполирования по Ньютону. Выполним в этих формулах замену переменной следующего вида:

• для первой интерполяционной формулы – 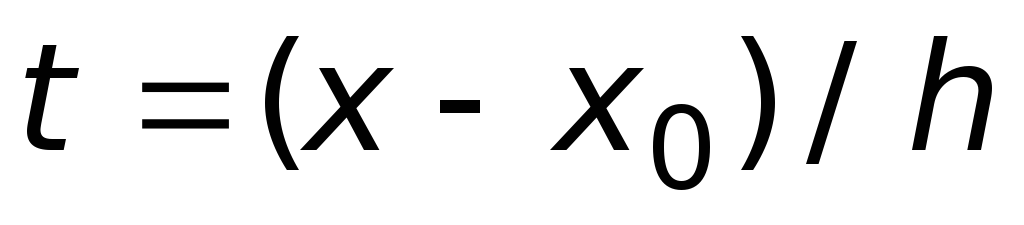, когда ;

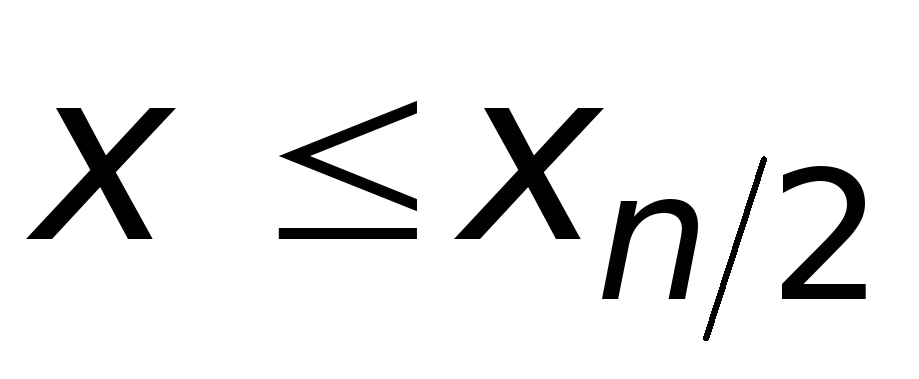• для второй интерполяционной формулы – 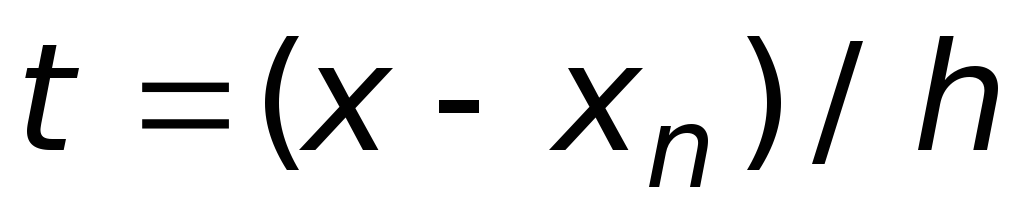, когда .

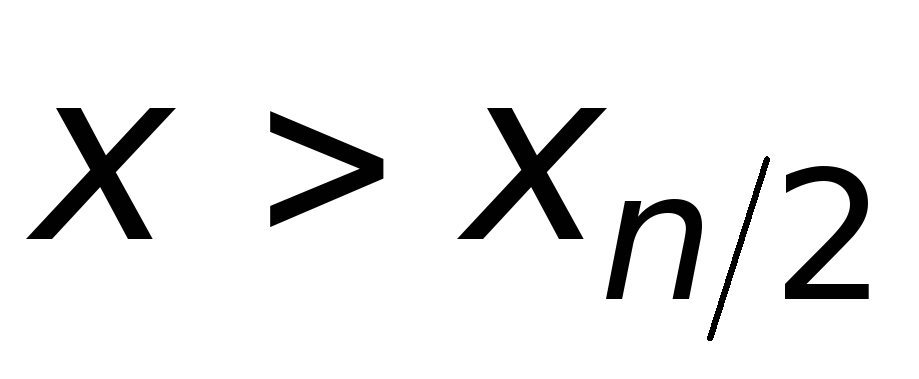Тогда будем иметь (с учетом того, что степень интерполяционного многочлена будет ):

, (11.16)

. (11.17)

Дифференцирование обеих формул дает следующие выражения:

, (11.18)

. (11.19)

Выше мы уже обсуждали вид производной от произведения нескольких сомножителей. В данном случае каждое из слагаемых (кроме первых) в суммах (11.18) и (11.19) содержит производную от произведения сомножителей, количество которых равно – «номеру» слагаемого в этой сумме. При этом, в отличие от случая Лагранжа, в этом произведении нет «отсутствующих» скобок.

Поэтому алгоритм вычисления слагаемых в суммах (11.18) и (11.19) будет проще:

для го слагаемого в (11.18) ; (11.20)

для го слагаемого в (11.19) . (11.21)

Следующее соображение касается построения таблицы конечных разностей. Поскольку степень интерполяционного многочлена задана, то нет смысла вычислять разности порядков, старше чем .

Теперь Вы можете приступать к непосредственному программированию по данной работе.